Chọn phát biểu sai trong các phát biểu sau:
Nếu ^xOt=^yOt và tia Ot nằm giữa hai tia Ox;Oy thì tia Ot là tia phân giác của ^xOy nên C sai, D đúng.
Cho Ot là tia phân giác của ^xOy. Biết ^xOy=1000, số đo của ^xOt là:
Vì tia Ot là tia phân giác của ^xOy thì ^xOt=^yOt=^xOy2=100∘2=50∘
Cho ^xOy là góc vuông có tia On là phân giác, số đo của ^xOn là:
Vì On là tia phân giác của ^xOy nên ^xOn=^nOy=^xOy2=90∘2=45∘
Cho tia On là tia phân giác của ^mOt. Biết ^mOn=700, số đo của ^mOt là:
Vì tia On là tia phân giác của ^mOt nên ^mOn=^nOt=^mOt2
⇒^mOt=2.^mOn=2.70∘=140∘.
Cho ^AOB=90∘ và tia OB là tia phân giác của góc AOC. Khi đó góc AOC là
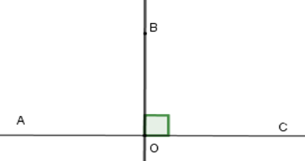
Vì tia OB là tia phân giác của góc AOC nên ^AOB=^BOC=^AOC2
Do đó ^AOC=2.^AOB=2.90∘=180∘
Nên góc AOC là góc bẹt.
Cho ^AOC=600. Vẽ tia OB sao cho OA là tia phân giác của ^BOC. Tính số đo của ^AOB và ^BOC.
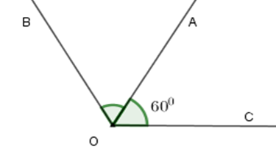
Vì tia OA là tia phân giác của ^BOC nên ta có
^AOB=^AOC=^BOC2 nên ^AOB=60∘;^BOC=2.^AOC=2.60∘=120∘
Vậy ^AOB=60∘;^BOC=120∘.
Cho ^AOB=1100 và ^AOC=550 sao cho ^AOB và ^AOC không kề nhau. Chọn câu sai.
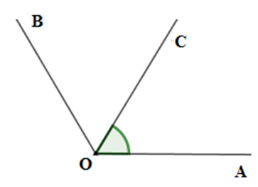
Vì ^AOB và ^AOC không kề nhau nên hai tia OC;OB thuộc cùng nửa mặt phẳng bờ là đường thẳng chứa tia OA. Lại có ^AOC<^AOB(55∘<110∘) nên tia OC nằm giữa hai tia OA và OB. (1)
Từ đó ^AOC+^COB=^AOB hay ^COB=^AOB−^AOC=110∘−55∘=55∘
Suy ra ^AOC=^BOC=55∘ (2)
Từ (1) và (2) suy ra tia OC là tia phân giác góc AOB.
Vậy A, B, D đúng và C sai.
Cho ^xOy và ^yOz là hai góc kề bù. Biết ^xOy=120∘ và tia Ot là tia phân giác của ^yOz. Tính số đo góc xOt.
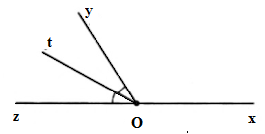
Vì ^xOy và ^yOz là hai góc kề bù nên ^xOy+^yOz=180∘ mà ^xOy=120∘ nên ^yOz=180∘−120∘=60∘.
Lại có tia Ot là tia phân giác của ^yOz nên ^zOt=12^yOz=12.60∘=30∘
Lại có ^zOt;^tOx là hai góc kề bù nên ^zOt+^tOx=180∘⇒^tOx=180∘−^zOt=180∘−30∘=150∘.
Vậy ^tOx=150∘.
Cho góc AOB và tia phân giác OC của góc đó. Vẽ tia phân giác OM của góc BOC. Biết ^BOM=35∘. Tính số đo góc AOB.
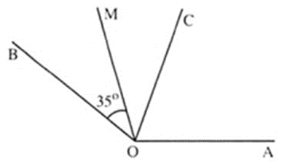
Vì tia OM là tia phân của góc BOC
nên ^BOC=2.^BOM=2.35∘=70∘
Lại có tia OC là tia phân giác của ^AOB nên ^AOB=2.^BOC=2.70∘=140∘. Vậy ^AOB=140∘.
Hai đường thẳng xy và x′y′ cắt nhau tại O. Biết ^xOx′=70o. Ot là tia phân giác của góc xOx’. Ot′ là tia đối của tia Ot. Tính số đo góc yOt′.
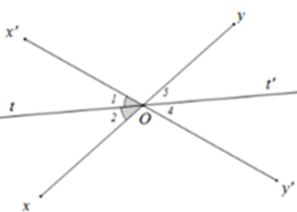
Vì Ot là tia phân giác của góc xOx′ nên
^xOt=^tOx′=12^xOx′=12.70o=35o
Vì Oy là tia đối của Ox,Ot′ là tia đối của Ot
⇒^yOt′=^xOt=35o (tính chất hai góc đối đỉnh).
Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy vẽ các tia Om;On sao cho ^xOm=a∘(a<180) và ^yOn=70∘. Với giá trị nào của a thì tia On là tia phân giác của ^yOm.
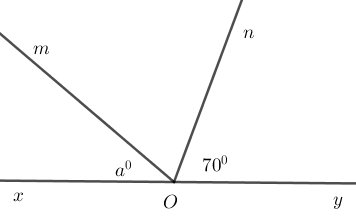
Giả sử tia On là tia phân giác của góc yOm thì ^mOy=2.^yOn=2.70∘=140∘.
Mà hai góc ^xOm;^yOm là hai góc kề bù nên ^xOm+^yOm=180∘⇒^xOm=180∘−^yOm =180∘−140∘=40∘.
Vậy a=40∘.
Hai đường thẳng AB và CD cắt nhau tại O tạo thành ^AOC=60∘ . Gọi OM là phân giác ^AOC và ON là tia đối của tia OM. Tính ^BON và ^DON.
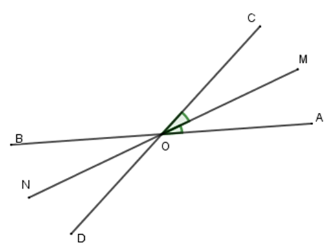
Vì AB và CD cắt nhau tại O nên OA và OB là hai tia đối nhau, OC và OD là hai tia đối nhau.
Vì OM là tia phân giác ^COA nên ^AOM=^COM=^COA2=602=30∘
Mà ON và OM là hai tia đối nhau nên ^AOM và ^BON là hai góc đối đỉnh; ^COM và ^DON là hai góc đối đỉnh
Suy ra ^AOM=^BON=30∘;^COM=^DON=30∘ hay ^BON=^DON=30∘.
Cho hai góc kề bù ^AOB;^BOC. Vẽ tia phân giác OM của góc BOA . Biết số đo góc MOC gấp 5 lần số đo góc AOM. Tính số đo góc BOC.
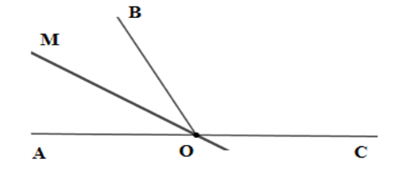
Vì hai góc kề bù ^AOB;^BOC nên ^AOC=180∘ hay OA;OC là hai tia đối nhau.
Suy ra hai góc ^MOC;^MOA là hai góc kề bù nên ^MOA+^MOC=180∘ mà ^MOC=5.^MOA (gt)
Nên ^MOA+5.^MOA=180∘⇒6.^MOA=180∘ suy ra ^MOA=180∘:6=30∘
Mà tia phân giác OM của góc BOA nên ^BOA=2.^MOA=2.30∘=60∘
Lại có hai góc kề bù ^AOB;^BOC nên ^AOB+^BOC=180∘ suy ra ^BOC=180∘−^AOB=180∘−60∘=120∘
Vậy ^BOC=120∘.

