Chọn câu đúng.
Ta có: N⊂Z⊂Q.
Do đó N⊂Q suy ra A đúng.
Chọn câu sai.
Ta có: 3∈Q nên A đúng.
53∈Q nhưng 53∉Z nên B sai.
03∈Q nên C đúng.
12∈Q;12∉N nên D đúng.
Số nào dưới đây là số hữu tỉ âm?
Ta có: 1113>0; −−1215=1215>0; −5−7=57>0; −215<0
Vậy số hữu tỉ âm là −215.
Với điều kiện nào của b thì phân số ab,a∈Z là số hữu tỉ?
Số hữu tỉ là số viết được dưới dạng phân số ab với a,b∈Z,b≠0.
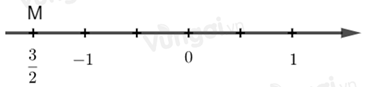
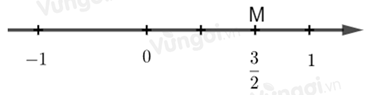
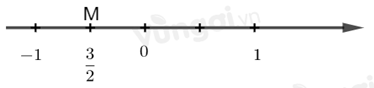
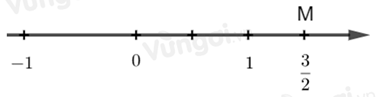
Số 32 được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) thành 2 phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng 12 đơn vị cũ.
+ Số 32 được biểu diễn bởi điểm M nằm bên phải điểm 0 và cách điểm 0 một đoạn bằng 3 đơn vị mới.

Trong các phân số sau, phân số nào không bằng phân số 25?
Ta có: 410=4:210:2=25;
−615=−615=−6:315:3=−25≠25;
−−410=410=4:210:2=25;
−6−15=615=6:315:3=25.
Vậy phân số không bằng phân số 25 là −615.
Sắp xếp các số hữu tỉ sau theo thứ tự tăng dần: 913;−1113;−1;413;−913;−1513;0.
Ta có: −1=−1313;0=013
Vì −15<−13<−11<−9<0<4<9
nên −1513<−1313<−1113<−913<013<413<913 hay −1513<−1<−1113<−913<0<413<913.
Số hữu tỉ nhỏ nhất trong các số 56;1112;2526;2930;89 là:
Phần bù với 1 của các số 56;1112;2526;2930;89 lần lượt là 16;112;126;130;19
Mà 30>26>12>9>6 nên 130<126<112<19<16
Suy ra 2930>2526>1112>89>56
Vậy số hữu tỉ nhỏ nhất là: 56.
So sánh hai số a=415 và b=−−821.
Ta có: a=415=4.715.7=28105;
b=−−821=821=8.521.5=40105
Vì 28<40⇒28105<40105 hay a<b.
So sánh x=20202021 và y=1000999.
Ta có: x=20202021<20212021=1 hay x<1;
y=1000999>999999=1 hay y>1
Từ đó suy ra y>1>x hay y>x.
Biểu diễn các số: 310; 2,5; 104; 620;0,3 bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
Ta có: 2,5=2510=25:510:5=52;
104=10:24:2=52;
620=6:220:2=310;
0,3=310.
Suy ra 310=620=0,3 và 2,5=104.
Vậy các số: 310; 2,5; 104; 620;0,3 được biểu diễn bởi hai điểm phân biệt trên cùng một trục số.
Trong các phân số 1422;7−11;21−33;2844;77121;−5535, có bao nhiêu phân số bằng phân số 711?
Ta có: 1422=14:222:2=711;
7−11=−711≠711;
21−33=−2133=−21:333:3=−711≠711;
2844=28:444:4=711;
77121=77:11121:11=711;
−5535=−55:535:5=−117≠711.
Vậy có ba phân số bằng phân số 711 là: 1422;2844;77121.
Cho số hữu tỉ x=2a−63(a∈Z). Với giá trị nào của a thì x là số nguyên dương.
Để số hữu tỉ x=2a−63 là số nguyên dương thì 2a−6>0 và (2a−6)⋮3.
Do (2a−6)⋮3 nên 2a−6=3k(k∈Z);
Mặt khác 2a−6>0 ⇒3k>0 ⇒k>0(k∈Z) tức là k∈N∗.
Vậy a=6+3k2(k∈N∗) thì x là số nguyên dương.
Cho số hữu tỉ y=9−12a2020. Với giá trị nào của a thì y không là số dương và cũng không là số âm.
Vì số hữu tỉ 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm nên để y=9−12a2020 không là số dương và cũng không là số âm thì y=0 ⇒9−12a2020=0 ⇒9−12a=0⇒12a=9⇒a=34.
Chọn câu sai:
Ta có: N∗⊂N⊂Z⊂Q
Từ đó có đáp án A, B, D đúng và C sai.
Sắp xếp các số hữu tỉ sau theo thứ tự tăng dần: −1;−10−22;933;−8−11;1;3555
Ta có:
−10−22=511933=311−8−11=8113555=711⇒−1<311<511<711<811<1Hay−1<933<1022<3555<811<1
Sắp xếp theo thứ tự tăng dần ta được: −1;933;−10−22;3555;−8−11;1
Chọn D
Cho các câu sau:
(I) Số hữu tỉ dương lớn hơn 0
(II) Số hữu tỉ dương lớn hơn số tự nhiên
(III) Số 0 là số hữu tỉ dương
(IV) Số nguyên dương là số hữu tỉ.
Số các câu đúng trong các câu trên là
(I) đúng
(II) sai vì số hữu tỉ dương chưa chắc lớn hơn số tự nhiên. Ví dụ: 54<2 .
(III) sai vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm
(IV) đúng vì mọi số nguyên dương đều là số hữu tỉ với mẫu số là 1.
Vậy có hai câu đúng.
Vì số hữu tỉ 0 không là số dương cũng không là số âm nên để y=4a−8−2021 không dương cũng không âm thì
y=0 suy ra 4a−8−2021=0 ⇒4a−8=0⇒a=2 .
Để x=a−57 là số nguyên dương thì (a−5)>0 và (a−5)⋮7
Giả sử a−5=7k(k∈N∗) suy ra a=5+7k(k∈N∗)
Trong các phân số: −1539;1026;−2565;3578;−7−26 có bao nhiêu phân số bằng phân số −513:
Ta có:
−1539=−513; −2565=−513.
Mà: −7−26=726 nên các phân số 1026;3578;−7−26 đều là các phân số dương
−513 là phân số âm
=> Các phân số 1026;3578;−7−26 không bằng −513
Vậy có 2 phân số bằng phân số −513 là: −1539; −2565