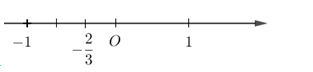
Biểu diễn các số: \(\dfrac{{ - 4}}{{ - 8}};\,\,0,2;\,\,\dfrac{3}{15};\,\dfrac{3}{6}\) bởi các điểm trên cùng một trục số ta được bao nhiêu điểm phân biệt?
Ta có:
\(\dfrac{{ - 4}}{{ - 8}} = \dfrac{1}{2}\); \(0,2 = \dfrac{2}{{10}} = \dfrac{1}{5}\); \(\dfrac{3}{{15}} = \dfrac{1}{5}\); \(\dfrac{3}{6} = \dfrac{1}{2}\)
Nên: \(\dfrac{{ - 4}}{{ - 8}} = \dfrac{3}{6} = \dfrac{1}{2}\)
\(0,2 = \dfrac{3}{{15}} = \dfrac{1}{5}\)
Do đó các số \(\dfrac{{ - 4}}{{ - 8}};\,\,0,2;\,\,\dfrac{3}{15};\,\dfrac{3}{6}\) được biểu diễn bởi hai điểm trên trục số.
Ta có \(x = \dfrac{{2022}}{{2021}} > \dfrac{{2021}}{{2021}} = 1\) hay \(x > 1\)
Và \(y = \dfrac{{15}}{{16}} < \dfrac{{16}}{{16}} = 1\) hay \(y < 1\)
Từ đó suy ra \(x > 1 > y\) hay \(x > y\) .
So sánh hai phân số: \(x = \frac{{11}}{{ - 24}}\) và \(y = \frac{{ - 7}}{{18}}\).
Ta có: \(x = \dfrac{{11}}{{ - 24}} = \dfrac{{11.( - 3)}}{{ - 24.( - 3)}} = \dfrac{{ - 33}}{{72}}\)
\(y = \dfrac{{ - 7}}{{18}}\dfrac{{ - 7.4}}{{18.4}} = \dfrac{{ - 28}}{{72}}\)
Mà \( - 33 < - 28\) nên \(\dfrac{{ - 33}}{{72}} < \dfrac{{ - 28}}{{72}}\).
Vậy \(x < y\).
Phần bù với \(1\) của các số \(\dfrac{12}{13};\dfrac{4}{5};\dfrac{9}{10};\dfrac{{14}}{{15}};\dfrac{{40}}{{41}}\) lần lượt là \(\dfrac{1}{13};\,\dfrac{1}{5};\dfrac{1}{10};\dfrac{1}{{15}};\dfrac{1}{{41}}\)
Mà \(41 > 15 > 13 > 10 > 5\) nên \(\dfrac{1}{{41}} < \dfrac{1}{{15}} < \dfrac{1}{13} < \dfrac{1}{10} < \dfrac{1}{5}\)
Suy ra \(\dfrac{{40}}{{41}} > \dfrac{{14}}{{15}} > \dfrac{12}{13} > \dfrac{9}{10} > \dfrac{4}{5}\)
Số hữu tỉ lớn nhất là: \(\dfrac{{40}}{{41}}\)
Cho các câu sau:
(I) Số hữu tỉ dương lớn hơn 0
(II) Số hữu tỉ âm bé hơn số tự nhiên
(III) Số $0$ không là số hữu tỉ
(IV) Số nguyên âm là số hữu tỉ.
Số các câu sai trong các câu trên là:
(I) đúng
(II) đúng
(III) sai vì số hữu tỉ bao gồm cả số 0
(IV) đúng vì mọi số nguyên dương đều là số hữu tỉ với mẫu số là \(1\).
Vậy có 1 câu sai.
Ta có: \(\)\(\dfrac{{ - 10}}{{18}} = \dfrac{{ - 5}}{9}\); \(\dfrac{{15}}{{ - 27}} = \dfrac{{ - 5}}{9}\); \(\dfrac{{ - 25}}{{ - 45}} = \dfrac{5}{9}\); \(\dfrac{{20}}{{ - 36}} = \dfrac{{ - 5}}{9}\)
Vậy phân số không bằng phân số \(\dfrac{{ - 5}}{9}\) là \(\dfrac{{ - 25}}{{ - 45}}\).
+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm \(0\) đến điểm \(-1\)) thành \(3\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{3}\) đơn vị cũ.
+ Số \(\dfrac{-1}{3}\) được biểu diễn bởi điểm \(M\) nằm bên Trái điểm \(0\) và cách điểm \(0\) một đoạn bằng \(1\) đơn vị mới.
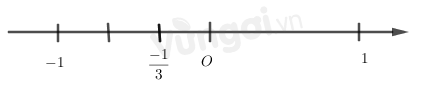
+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm \(0\) đến điểm \(-1\)) thành \(3\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{3}\) đơn vị cũ.
+ Số \(\dfrac{-1}{3}\) được biểu diễn bởi điểm \(M\) nằm bên Trái điểm \(0\) và cách điểm \(0\) một đoạn bằng \(1\) đơn vị mới.

+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm \(0\) đến điểm \(-1\)) thành \(3\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{3}\) đơn vị cũ.
+ Số \(\dfrac{-1}{3}\) được biểu diễn bởi điểm \(M\) nằm bên Trái điểm \(0\) và cách điểm \(0\) một đoạn bằng \(1\) đơn vị mới.

+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm \(0\) đến điểm \(-1\)) thành \(3\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{3}\) đơn vị cũ.
+ Số \(\dfrac{-1}{3}\) được biểu diễn bởi điểm \(M\) nằm bên Trái điểm \(0\) và cách điểm \(0\) một đoạn bằng \(1\) đơn vị mới.

+ Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm \(0\) đến điểm \(-1\)) thành \(3\) phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\dfrac{1}{3}\) đơn vị cũ.
+ Số \(\dfrac{-1}{3}\) được biểu diễn bởi điểm \(M\) nằm bên Trái điểm \(0\) và cách điểm \(0\) một đoạn bằng \(1\) đơn vị mới.

Với điều kiện nào của \(a\) thì phân số \(\frac{a}{b};\,\,b \in \mathbb{Z},\,b \ne 0\) là số hữu tỉ?
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) trong đó \(a,b \in Z\,;b \ne 0.\)
Vậy \(a \in \mathbb{Z}\).
Ta có:
\(\frac{{ - 3}}{{ - 11}} = \frac{3}{{11}} > 0\)
\(\frac{{ - 9}}{4} < 0\); \(\frac{4}{{ - 7}} < 0\); \(\frac{{32}}{{ - 13}} < 0\).
Vậy \(\frac{{ - 3}}{{ - 11}}\) là số hữu tỉ dương.
Ta có:
\(\dfrac{{ - 2}}{{ - 5}} \in \mathbb{Q}\) nên A đúng.
\(\dfrac{{ - 2}}{{ - 3}} \notin \mathbb{Z}\) nên B sai.
\( - 5 \in \mathbb{Q}\) nên C sai.
\(\dfrac{{ - 7}}{9} \notin \mathbb{Z}\) nên D sai.
Tập hợp số hữu tỉ được kí hiệu là
Tập hợp các số hữu tỉ được kí hiệu là $Q.$
Tập hợp các số tự nhiên kí hiệu là $N.$
Tập hợp số tự nhiên khác $0$ kí hiệu là $N^*$
Chọn câu đúng
Ta có \( - 6 \in \mathbb{Z};-6\notin\mathbb N \) nên D sai.
\(\dfrac{2}{3} \in \mathbb{Q};\,\dfrac{2}{3} \notin \mathbb{Z}\) nên B sai.
\( - \dfrac{9}{2} \in \mathbb{Q}\) nên C sai
\(\dfrac{3}{2} \in \mathbb{Q}\) nên A đúng.
Số nào dưới đây là số hữu tỉ dương?
\(\begin{array}{l}\dfrac{{ - 2}}{{ - 3}} = \dfrac{2}{3} > 0\,;\\\dfrac{{ - 2}}{5}\, < 0\,;\,\dfrac{{ - 5}}{{15}} < 0\,\,;\,\dfrac{2}{{ - 15}} < 0.\end{array}\)
Vậy số hữu tỉ dương là \(\dfrac{{ - 2}}{{ - 3}}.\)
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) với:
Số hữu tỉ là số được viết dưới dạng phân số \(\dfrac{a}{b}\) trong đó \(a,b \in Z\,;b \ne 0.\)
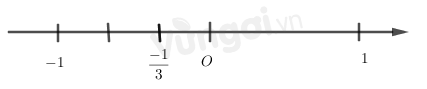
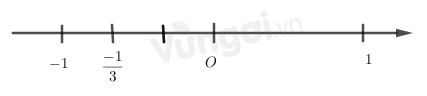
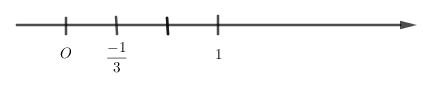
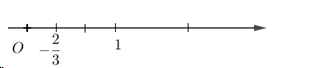
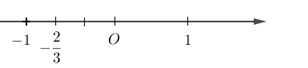
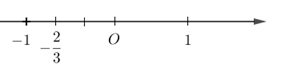
Số \( - \dfrac{2}{3}\) được biểu diễn trên trục số bởi hình vẽ nào dưới đây?
Biểu diễn số \( - \dfrac{2}{3}\) trên trục số ta được:
Trong các phân số sau, phân số nào không bằng phân số $\dfrac{3}{4}$?
\(\dfrac{6}{9} = \dfrac{2}{3}\,;\,\dfrac{9}{{12}} = \dfrac{3}{4}\,;\,\dfrac{{ - 6}}{{ - 8}} = \dfrac{3}{4}\,;\,\dfrac{{ - 3}}{{ - 4}} = \dfrac{3}{4}.\)
Vậy phân số không bằng phân số $\dfrac{3}{4}$ là \(\dfrac{6}{9}.\)