Chọn câu đúng.
- Đường trung tuyến của tam giác là đoạn thẳng nối đỉnh của tam giác với trung điểm của cạnh đối diện nên A đúng.
- Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó nên B, C đúng.
Cho tam giác \(ABC\) có \(G\) là trọng tâm tam giác, \(N\) là trung điểm \(AC\). Khi đó \(BG = ...BN\). Số thích hợp điền vào chỗ trống là:

Vì \(G\) là trọng tâm của \(\Delta ABC\) nên \(BG = \dfrac{2}{3}BN\).
Số thích hợp điền vào chỗ trống là: \(\dfrac{2}{3}.\)
Biết \(GS = 1,5cm.\) Tính \(NG.\)
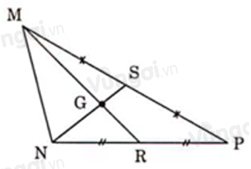
Theo câu trước ta có \(G\) là trọng tâm của tam giác \(MNP\).
Theo tính chất ba đường trung tuyến của tam giác ta có:
\(\dfrac{{NG}}{{NS}} = \dfrac{2}{3} \Rightarrow \dfrac{{NG}}{{GS}} = 2 \Rightarrow NG = 2GS = 2.1,5 = 3(cm)\).
Vậy \(NG = 3cm\).
Biết \(MG = 3cm.\) Tính \(MR.\)

Ta có: \(MR;NS\) là hai đường trung tuyến của tam giác \(MNP\) và chúng cắt nhau tại \(G\) nên \(G\) là trọng tâm của tam giác \(MNP\).
Theo tính chất ba đường trung tuyến của tam giác ta có:
\(\dfrac{{MG}}{{MR}} = \dfrac{2}{3} \Rightarrow MR = \dfrac{3}{2}MG = \dfrac{3}{2}.3 = 4,5(cm)\).
Vậy \(MR = 4,5cm\).
Biết \(MG = 3cm.\) Tính \(MR.\)

Ta có: \(MR;NS\) là hai đường trung tuyến của tam giác \(MNP\) và chúng cắt nhau tại \(G\) nên \(G\) là trọng tâm của tam giác \(MNP\).
Theo tính chất ba đường trung tuyến của tam giác ta có:
\(\dfrac{{MG}}{{MR}} = \dfrac{2}{3} \Rightarrow MR = \dfrac{3}{2}MG = \dfrac{3}{2}.3 = 4,5(cm)\).
Vậy \(MR = 4,5cm\).
Tam giác \(ABC\) có trung tuyến \(AM = 15\,cm\) và trọng tâm \(G\). Độ dài đoạn \(AG\) là:
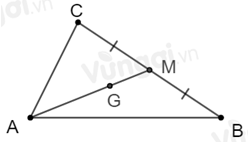
Vì \(G\) là trọng tâm của tam giác \(ABC\) và \(AM\) là đường trung tuyến nên \(AG = \dfrac{2}{3}AM\) (tính chất ba đường trung tuyến của tam giác).
Do đó \(AG = \dfrac{2}{3}.15 = 10\,cm.\)
Cho \(G\) là trọng tâm của tam giác đều \(ABC\). \(D,E,F\) lần lượt là trung điểm của \(BC,\,AC,\,AB.\) Chọn câu đúng.
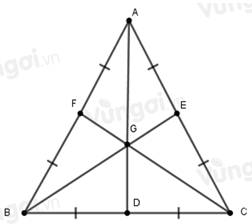
Vì \(D,E,F\) lần lượt là trung điểm của \(BC,\,AC,\,AB\) nên \(BD = DC = \dfrac{1}{2}BC;\) \(CE = EA = \dfrac{1}{2}AC;\) \(AF = FB = \dfrac{1}{2}AB.\)
Mặt khác: \(BC = AC = AB\) (do tam giác \(ABC\) là tam giác đều)
Do đó \(BD = DC = CE = EA = AF = FB\).
Xét \(\Delta AEB\) và \(\Delta AFC\) có: AB = AC; \(\widehat A\) chung; AE = AF.
Vậy \(\Delta AEB = AFC\,(c.g.c)\) suy ra: \(BE = CF\,\) (hai cạnh tương ứng) \(\left( 1 \right)\)
Chứng minh tương tự ta có \(\Delta BEC = ADC\,(c.g.c)\) suy ra \(BE = AD\) (hai cạnh tương ứng) \(\left( 2 \right)\)
Từ (1) và (2) ta có: \(AD = BE = CF\left( 3 \right)\)
Theo đề bài \(G\) là trọng tâm của tam giác \(ABC\) nên ta có:
\(GA = \dfrac{2}{3}AD;\,\,GB = \dfrac{2}{3}BE;\,\,GC = \dfrac{2}{3}CF\)\( \Rightarrow GD = \dfrac{1}{3}AD;\,\,GE = \dfrac{1}{3}BE;\,\,GF = \dfrac{1}{3}CF\)
Kết hợp với (3) ta được: \(GD = GE = GF\).
Cho tam giác \(ABC\) có các đường trung tuyến \(BD\) và \(CE\) vuông góc với nhau. Tính độ dài cạnh \(BC\) biết \(BD = 4,5\,cm;\,CE = 6\,cm.\)

Gọi giao điểm của hai đường trung tuyến \(BD\) và \(CE\) là \(G\) thì \(G\) là trọng tâm tam giác \(ABC.\)
Theo tính chất ba đường trung tuyến của tam giác ta có: \(BG = \dfrac{2}{3}BD;\,CG = \dfrac{2}{3}CE\)
Mà \(BD = 4,5\,cm;\,CE = 6\,cm\) nên \(BG = \dfrac{2}{3}.4,5 = 3\,cm;\,CG = \dfrac{2}{3}.6\, = 4\,cm.\)
Xét tam giác \(BGC\) vuông tại G (do \(BD\) và \(CE\) vuông góc với nhau tại G), theo định lý Py-ta-go ta có:
\(B{C^2} = B{G^2} + C{G^2}\)
\(B{C^2} = {3^2} + {4^2} = 25\) hay \(BC = 5\,cm.\)
Vậy \(BC = 5\,cm.\)
Cho tam giác \(ABC\), có \(G\) là trọng tâm và các đường trung tuyến \(AM,BN,CP\). Trên tia \(AG\) kéo dài lấy \(D\) sao cho \(G\) là trung điểm của \(AD.\) So sánh các cạnh của tam giác \(BGD\) với các đường trung tuyến của tam giác \(ABC.\)

\(\Delta ABC\) có \(G\) là trọng tâm và các đường trung tuyến \(AM,BN,CP\) nên theo tính chất ba đường trung tuyến của tam giác ta có:
\(AG = \dfrac{2}{3}AM;BG = \dfrac{2}{3}BN;\,CG = \dfrac{2}{3}CP\).
Vì \(G\) là trung điểm của \(AD\) nên \(GD = AG\) mà \(AG = \dfrac{2}{3}AM\, (cmt)\), do đó \(GD = \dfrac{2}{3}AM\)
Ta có: \(GD = AG = 2GM\) (tính chất ba đường trung tuyến của tam giác)
Mà \(GD = GM + MD \Rightarrow 2GM = GM + MD\) \( \Rightarrow GM = MD\)
Xét \(\Delta BMD\) và \(\Delta CMG\) có:
\(GM = MD\) (cmt)
\(\widehat {BMD} = \widehat {CMG}\) (hai góc đối đỉnh)
\(BM = MC\) (vì \(AM\) là đường trung tuyến của \(\Delta ABC\) )
Do đó \(\Delta BMD = \Delta CMG (c.g.c)\)
Suy ra \(BD = CG\) (hai cạnh tương ứng) mà \(CG = \dfrac{2}{3}CP\) (cmt) nên \(BD = \dfrac{2}{3}CP\)
Vậy \(BG = \dfrac{2}{3}BN\); \(GD = \dfrac{2}{3}AM\); \(BD = \dfrac{2}{3}CP\).
Cho tam giác \(ABC\), đường trung tuyến \(BD\). Trên tia đối của tia \(DB\) lấy điểm \(E\) sao cho \(DE = DB.\) Gọi \(M,N\) theo thứ tự là trung điểm của \(BC;CE.\) Gọi \(I;K\) theo thứ tự là giao điểm của \(AM,AN\) với \(BE.\) Tính \(BE\) biết \(IK = 3cm.\)

Ta có: \(DE = DB\) mà \(BD + DE = BE\) nên \(2BD = BE \Rightarrow BD = DE = \dfrac{1}{2}BE\).
Vì \(AM;BD\) là hai đường trung tuyến của tam giác \(ABC\) và chúng cắt nhau tại \(I\) nên \(I\) là trọng tâm của tam giác \(ABC\).
Khi đó \(BI = \dfrac{2}{3}BD = \dfrac{2}{3}.\dfrac{1}{2}BE = \dfrac{1}{3}BE\) \(\left( 1 \right)\)
Vì \(AN;ED\) là hai đường trung tuyến của tam giác \(ACE\) và chúng cắt nhau tại \(K\) nên \(K\) là trọng tâm tam giác \(ACE\) nên \(EK = \dfrac{2}{3}ED = \dfrac{2}{3}.\dfrac{1}{2}BE = \dfrac{1}{3}BE\,\,\,\left( 2 \right)\)
Mặt khác \(BI + IK + KE = BE\) kết hợp với \(\left( 1 \right);\left( 2 \right)\) suy ra \(\dfrac{1}{3}BE + IK + \dfrac{1}{3}BE = BE \Rightarrow IK = \dfrac{1}{3}BE\).
Do đó \(BE = 3IK = 3.3 = 9cm\).
Cho tam giác \(ABC\) vuông tại \(A\) có: \(AC = 9cm,\,BC = 15cm\). Ba đường trung tuyến \(AM,BN,CE\) cắt nhau tại \(O.\) Độ dài trung tuyến \(CE\) là:

\(\Delta ABC\) vuông tại \(A\) nên theo định lí Py-ta-go ta có:
\(A{B^2} + A{C^2} = B{C^2}\,\,\, \Rightarrow A{B^2} = B{C^2} - A{C^2}\)
Mà \(AC = 9cm,BC = 15cm\)\( \Rightarrow A{B^2} = {15^2} - {9^2} = 144 \Rightarrow AB = 12\,cm\)
Ta có: \(AM,BN,CE\) là các đường trung tuyến ứng với các cạnh \(BC,AC,AB\) của tam giác vuông \(ABC\)
Suy ra \(M,N,E\) lần lượt là trung điểm của các cạnh \(BC,AC,AB.\)
Do đó \({\rm{AE}} = \dfrac{1}{2}AB = \dfrac{1}{2} \cdot 12 = 6cm\)
Áp dụng định lí Py-ta-go với tam giác \(ACE\) vuông tại \(A\) ta có: \(A{C^2} + A{E^2} = C{E^2} \Rightarrow {9^2} + {6^2} = C{E^2} \Rightarrow C{E^2} = 117\)\( \Rightarrow CE = \sqrt {117} \,cm\).
Cho tam giác \(MNP,\) hai đường trung tuyến \(ME\) và \(NF\) cắt nhau tại \(O.\) Tính diện tích tam giác \(MNP,\) biết diện tích tam giác \(MNO\) là \(12c{m^2}\).
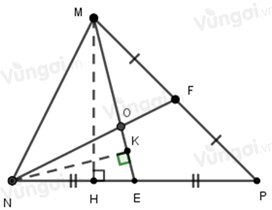
Gọi \(MH\) là đường cao kẻ từ \(M\) xuống cạnh \(NP;NK\) là đường cao kẻ từ \(N\) xuống cạnh \(ME.\)
Hai đường trung tuyến \(ME\) và \(NF\) cắt nhau tại \(O\) nên \(O\) là trọng tâm tam giác \(MNP,\) do đó \(MO = \dfrac{2}{3}ME\).
Có \(ME\) là đường trung tuyến ứng với cạnh \(NP\) nên \(E\) là trung điểm của \(NP,\) suy ra: \(NP = 2.NE\)
Ta có:
\(\dfrac{{{S_{MNO}}}}{{{S_{MNE}}}} = \dfrac{{\dfrac{1}{2}.NK.MO}}{{\dfrac{1}{2}.NK.ME}} = \dfrac{{\dfrac{1}{2}.NK.\dfrac{2}{3}.ME}}{{\dfrac{1}{2}.NK.ME}} = \dfrac{2}{3}\,\,\,\,\,\,\,\,\, \Rightarrow {S_{MNE}} = \dfrac{3}{2}{S_{MNO}}\)
\(\dfrac{{{S_{MNE}}}}{{{S_{MNP}}}} = \dfrac{{\dfrac{1}{2}.MH.NE}}{{\dfrac{1}{2}.MH.NP}} = \dfrac{{\dfrac{1}{2}.MH.NE}}{{\dfrac{1}{2}.MH.2.NE}} = \dfrac{1}{2}\,\,\,\,\,\,\,\,\, \Rightarrow {S_{MNP}} = 2{S_{MNE}}\)
Từ đó suy ra:
\({S_{MNP}} = 2.{S_{MNE}} = 2.\dfrac{3}{2}.{S_{MNO}} = 3.{S_{MNO}} \Rightarrow {S_{MNP}} = 3.12 = 36\,c{m^2}\).
Chọn câu đúng.
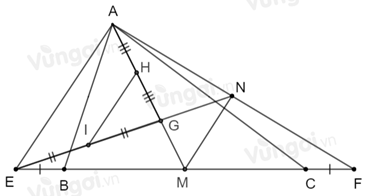
Theo câu trước ta có: \(G\) là trọng tâm \(\Delta AEF\) nên \(EG = \dfrac{2}{3}EN\) (tính chất ba đường trung tuyến của tam giác)
Mà \(GI = \dfrac{1}{2}EG\) (vì \(I\) là trung điểm của \(EG\))
Suy ra \(GI = \dfrac{1}{2}.\dfrac{2}{3}EN = \dfrac{1}{3}EN\)
Mặt khác \(GN = \dfrac{1}{3}EN\) (vì \(G\) là trọng tâm \(\Delta AEF\))
Do đó \(GI = GN\).
Theo câu trước ta có: \(AG = \dfrac{2}{3}AM\) mà \(GH = \dfrac{1}{2}AG\) (vì \(H\) là trung điểm của \(AG\))
Suy ra \(GH = \dfrac{1}{2}.\dfrac{2}{3}AM = \dfrac{1}{3}AM\)
Mặt khác \(GM = \dfrac{1}{3}AM\) (vì \(G\) là trọng tâm \(\Delta AEF\))
Do đó \(GH = GM\).
Xét \(\Delta GHI\) và \(\Delta GMN\) có:
\(GI = GN\) (cmt)
\(\widehat {HGI} = \widehat {NGM}\) (hai góc đối đỉnh)
\(GH = GM\) (cmt)
Vậy \(\Delta GHI = \Delta GMN\,(c.g.c)\) \(\Rightarrow HI = MN\) (hai cạnh tương ứng); \(\widehat {IHG} = \widehat {NMG}\) (hai góc tương ứng)
Mà \(\widehat {IHG};\widehat {NMG}\) ở vị trí so le trong nên \(HI//MN\).
Chọn câu đúng.
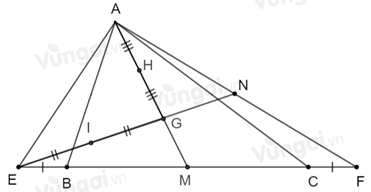
Ta có: \(MB = MC\) (vì \(AM\) là đường trung tuyến ứng với cạnh \(BC\) của \(\Delta ABC)\); \(BE = CF\) (gt)
Mà \(ME = MB + BE;MF = MC + CF\)
Suy ra \(ME = MF\).
Do đó \(AM\) là đường trung tuyến ứng với cạnh \(EF\) của \(\Delta AEF\)
Mặt khác \(AG = \dfrac{2}{3}AM\) (do G là trọng tâm \(\Delta ABC)\)
Vậy G là trọng tâm \(\Delta AEF\).
Chọn câu đúng.

Ta có: \(MB = MC\) (vì \(AM\) là đường trung tuyến ứng với cạnh \(BC\) của \(\Delta ABC)\); \(BE = CF\) (gt)
Mà \(ME = MB + BE;MF = MC + CF\)
Suy ra \(ME = MF\).
Do đó \(AM\) là đường trung tuyến ứng với cạnh \(EF\) của \(\Delta AEF\)
Mặt khác \(AG = \dfrac{2}{3}AM\) (do G là trọng tâm \(\Delta ABC)\)
Vậy G là trọng tâm \(\Delta AEF\).
Điền số thích hợp vào chỗ chấm: $AG = \ldots GD$
Theo câu trước ta có $G$ là trọng tâm của tam giác \(ABC\) .
Theo tính chất ba đường trung tuyến của tam giác ta có : \(\dfrac{{AG}}{{AD}} = \dfrac{2}{3} \Rightarrow \dfrac{{AG}}{{GD}} = 2 \Rightarrow AG = 2GD\).
Vậy số thích hợp điền vào chỗ chấm là $2.$
Điền số thích hợp vào chỗ chấm: \(BG = ...BE\)
Ta có $AD;BE$ và $CF$ là ba đường trung tuyến của tam giác $ABC$ và chúng cắt nhau tại $G$ nên $G$ là trọng tâm của tam giác \(ABC\) .
Theo tính chất ba đường trung tuyến của tam giác ta có : \(\dfrac{{BG}}{{BE}} = \dfrac{2}{3} \Rightarrow BG = \dfrac{2}{3}BE\).
Vậy số thích hợp điền vào chỗ chấm là \(\dfrac{2}{3}.\)
Điền số thích hợp vào chỗ chấm: \(BG = ...BE\)
Ta có $AD;BE$ và $CF$ là ba đường trung tuyến của tam giác $ABC$ và chúng cắt nhau tại $G$ nên $G$ là trọng tâm của tam giác \(ABC\) .
Theo tính chất ba đường trung tuyến của tam giác ta có : \(\dfrac{{BG}}{{BE}} = \dfrac{2}{3} \Rightarrow BG = \dfrac{2}{3}BE\).
Vậy số thích hợp điền vào chỗ chấm là \(\dfrac{2}{3}.\)
Điền số thích hợp vào chỗ chấm: \(BG = ...BE\)
Ta có $AD;BE$ và $CF$ là ba đường trung tuyến của tam giác $ABC$ và chúng cắt nhau tại $G$ nên $G$ là trọng tâm của tam giác \(ABC\) .
Theo tính chất ba đường trung tuyến của tam giác ta có : \(\dfrac{{BG}}{{BE}} = \dfrac{2}{3} \Rightarrow BG = \dfrac{2}{3}BE\).
Vậy số thích hợp điền vào chỗ chấm là \(\dfrac{2}{3}.\)
Chọn câu sai.
+ Một tam giác chỉ có một trọng tâm nên đáp án D sai.

