Cho \(G\) là trọng tâm của tam giác đều \(ABC\). \(D,E,F\) lần lượt là trung điểm của \(BC,\,AC,\,AB.\) Chọn câu đúng.

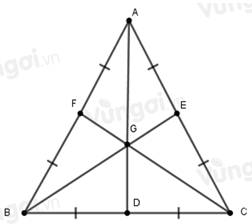
Vì \(D,E,F\) lần lượt là trung điểm của \(BC,\,AC,\,AB\) nên \(BD = DC = \dfrac{1}{2}BC;\) \(CE = EA = \dfrac{1}{2}AC;\) \(AF = FB = \dfrac{1}{2}AB.\)

Mặt khác: \(BC = AC = AB\) (do tam giác \(ABC\) là tam giác đều)

Do đó \(BD = DC = CE = EA = AF = FB\).

Xét \(\Delta AEB\) và \(\Delta AFC\) có: AB = AC; \(\widehat A\) chung; AE = AF.

Vậy \(\Delta AEB = AFC\,(c.g.c)\) suy ra: \(BE = CF\,\) (hai cạnh tương ứng) \(\left( 1 \right)\)

Chứng minh tương tự ta có \(\Delta BEC = ADC\,(c.g.c)\) suy ra \(BE = AD\) (hai cạnh tương ứng) \(\left( 2 \right)\)

Từ (1) và (2) ta có: \(AD = BE = CF\left( 3 \right)\)

Theo đề bài \(G\) là trọng tâm của tam giác \(ABC\) nên ta có:

\(GA = \dfrac{2}{3}AD;\,\,GB = \dfrac{2}{3}BE;\,\,GC = \dfrac{2}{3}CF\)\( \Rightarrow GD = \dfrac{1}{3}AD;\,\,GE = \dfrac{1}{3}BE;\,\,GF = \dfrac{1}{3}CF\)

Kết hợp với (3) ta được: \(GD = GE = GF\).