Trả lời bởi giáo viên
Đáp án đúng: d
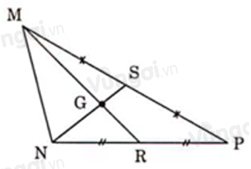
Ta có: \(MR;NS\) là hai đường trung tuyến của tam giác \(MNP\) và chúng cắt nhau tại \(G\) nên \(G\) là trọng tâm của tam giác \(MNP\).
Theo tính chất ba đường trung tuyến của tam giác ta có:
\(\dfrac{{MG}}{{MR}} = \dfrac{2}{3} \Rightarrow MR = \dfrac{3}{2}MG = \dfrac{3}{2}.3 = 4,5(cm)\).
Vậy \(MR = 4,5cm\).
Hướng dẫn giải:
Sử dụng định lý về tính chất ba đường trung tuyến của một tam giác:
+ Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.
+ Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng \(\dfrac{2}{3}\) độ dài đường trung tuyến đi qua đỉnh ấy.
Câu hỏi khác
- Bài tập mối quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu toán 7 có lời giải
- Bài tập về ba đường trung tuyến của tam giác toán 7 có lời giải
- Bài tập quan hệ giữa góc và cạnh đối diện trong một tam giác toán 7 có lời giải
- Bài tập quan hệ giữa ba cạnh của một tam giác toán 7 có lời giải
- Bài tập về ba đường phân giác của tam giác toán 7 có lời giải
