Em hãy chọn cụm từ thích hợp điển vào chỗ trống:
“Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì …”
Trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn.
Cho ba điểm \(A,\,B,\,C\) thẳng hàng, \(B\) nằm giữa \(A\) và \(C\). Trên đường thẳng vuông góc với \(AB\) tại \(B\) ta lấy điểm \(M\). So sánh \(MB\) và \(MC,\,MB\) và \(MA.\)

Vì \(MB\) là đường vuông góc và \(MA,\,MC\) là đường xiên nên \(MA > MB;\,MC > MB\) (quan hệ giữa đường vuông góc và đường xiên).
Trong tam giác \(ABC\) có \(AH\) vuông góc với \(BC\,\left( {H \in BC} \right)\). Chọn câu sai.
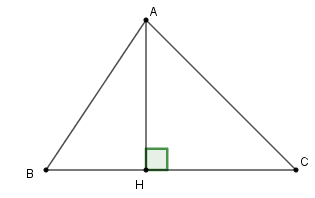
Trong tam giác \(ABC\) có \(AH\) là đường vuông góc và \(BH;CH\) là hai hình chiếu.
Khi đó
+ Nếu \(AB < AC\) thì \(BH < HC\) (A đúng)
+ Nếu \(AB > AC\) thì \(BH > HC\) ( B sai)
+ Nếu \(AB = AC\) thì \(BH = HC\) (C đúng)
+ Nếu \(HB > HC\) thì \(AB > AC\) (D đúng)
Cho hình vẽ sau:

Em hãy chọn khẳng định sai trong các khẳng định sau:
Vì \(OH\) là đường vuông góc và \(OM,\,ON\) là đường xiên nên \(OH < OM;\,OH < ON\) (quan hệ giữa đường vuông góc và đường xiên).
Vì \(M\) nằm giữa hai điểm \(H\) và \(N\) nên \(HM < HN\) suy ra \(OM < ON\) (quan hệ giữa đường xiên và hình chiếu).
\(\Delta OHM\) vuông tại \(H\) nên \(\widehat {HMO}\) là góc nhọn hay \(\widehat {HMO} < {90^o}\).
Mặt khác \(\widehat {HMO} + \widehat {OMN} = {180^o}\) (hai góc kề bù)
\( \Rightarrow \widehat {OMN} > {180^o} - {90^o}\)
\( \Rightarrow \widehat {OMN} > {90^o}\) hay \(\widehat {OMN}\) là góc tù.
Xét \(\Delta OMN\) có \(\widehat {OMN}\) là góc tù nên \(\widehat {OMN} > \widehat {MNO}\).
Vậy đáp án D sai.
Cho \(\Delta ABC\) vuông tại \(A,M\) là trung điểm của \(AC.\) Gọi \(D,E\) lần lượt là hình chiếu của A và C xuống đường thẳng \(BM.\) Chọn câu đúng nhất.
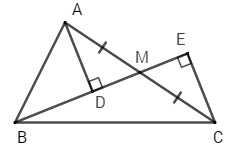
Vì \(M\) là trung điểm của \(AC\) (gt) \( \Rightarrow AM = MC\) (tính chất trung điểm)
Xét tam giác vuông \(ADM\) và tam giác vuông \(CEM\) có:
\(AM = MC\left( {cmt} \right)\)
\(\widehat {AMD} = \widehat {EMC}\) (đối đỉnh)
\( \Rightarrow \Delta ADM = \Delta CEM\) (cạnh huyền – góc nhọn).
\( \Rightarrow AD = CE\) (hai cạnh tương ứng)
Xét \(\Delta ABD\) vuông tại \(D\) nên \(AD < AB\).
\( \Rightarrow 2AD < 2AB \Rightarrow AD + AD < 2AB\) hay \(AD+CE<2AB\) (A đúng).
\(\Delta ADM\) vuông tại \(D\) nên \(AD < AM\) (1)
\(\Delta CEM\) vuông tại \(E\) nên \(EC < CM\) (2)
Cộng (1) với (2) theo vế với vế ta được:
\(AD + EC < AM + CM\) hay \(AD + EC < AC\) (B đúng).
Vậy cả A, B đều đúng.
Cho \(\Delta ABC\) có \(CE\) và \(BD\) là hai đường vuông góc \(\left( {E \in AB,\,D \in AC} \right)\). So sánh \(BD + CE\) và \(2BC\)?

Vì \(BD\) và \(BC\) lần lượt là đường vuông góc và đường xiên kẻ từ \(B\) đến \(AC\) nên \(BD < BC\) (1)
Vì \(CE\) và \(BC\) lần lượt là đường vuông góc và đường xiên kẻ từ \(C\) đến \(AB\) nên \(CE < BC\) (2)
Cộng (1) với (2) theo vế với vế ta được:
\(BD + CE < BC + BC\) hay \(BD + CE < 2BC.\)
Cho \(\Delta ABC\) có \({90^0} < \widehat A < {180^0}.\) Trên cạnh \(AB\) và \(AC\) lấy tương ứng hai điểm \(M\) và \(N\) (\(M,N\) không trùng với các đỉnh của \(\Delta ABC\)). Chọn đáp án đúng nhất.

Từ \(B\) kẻ \(BH\) vuông góc đến \(AC\), vì \(\widehat {BAC}\) là góc tù nên \(H\) nằm ngoài đoạn thẳng \(AC.\)
Khi đó \(BA,BN,BC\) là các đường xiên kẻ từ \(B\) đến \(AC\), \(HA,HN,HC\) lần lượt là các hình chiếu của \(BA,BN,BC\) trên \(AC.\)
Ta có \(HA < HN < HC\) nên \(BA < BN < BC\) (quan hệ giữa đường xiên và hình chiếu).
Từ \(C\) kẻ \(CK\) vuông góc đến \(AC\), vì \(\widehat {BAC}\) là góc tù nên \(K\) nằm ngoài đoạn thẳng \(AB.\)
Khi đó \(CA,CM,CB\) là các đường xiên kẻ từ \(C\) đến \(AB\); \(KA,KM,KB\) lần lượt là các hình chiếu của \(CA,CM,CB\) trên \(AB.\)
Ta có \(KA < KM < KB\) nên \(CA < CM < CB\) (quan hệ giữa đường xiên và hình chiếu).
Chọn D.
Xác định vị trí điểm \(M\) sao cho \(d\) có giá trị lớn nhất

Sử dụng kết quả câu trước ta có \(d \le BC\) nên \(d\) có giá trị lớn nhất bằng \(BC\) khi \(AM \bot BC\) hay \(M\) là hình chiếu của \(A\) trên \(BC.\)
So sánh \(d\) và \(BC.\)
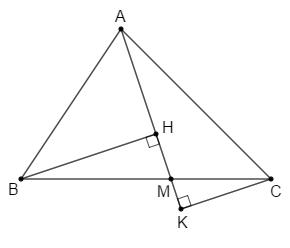
Kẻ \(BH \bot AM;\,CK \bot AM\) \(\left( {H,K \in AM} \right)\).
Theo đề bài ta có \(d = BH + CK\)
+ Trường hợp 1: Nếu \(AM\) không vuông góc với \(BC\) khi đó:
\(BH,\,BM\) lần lượt là đường vuông góc và đường xiên kẻ từ \(B\) đến \(AM\) suy ra \(BM > BH\) (1)
\(CK,\,CM\) lần lượt là đường vuông góc và đường xiên kẻ từ \(C\) đến \(AM\) suy ra \(CM > CK\) (2)
Cộng (1) với (2) theo vế với vế ta được:
\(BM + CM > BH + CK\) hay \(BC > d.\)
+ Trường hợp 2: Nếu \(AM\, \bot \,BC\)khi đó \(H,\,M,\,K\) trùng nhau.
Tam giác \(ABC\) có hai góc \(B,C\) nhọn nên \(M\) nằm giữa hai điểm \(B\) và \(C\) do đó \(BH + CK = BM + CM\) hay \(BC = d\).
Vậy \(d \le BC\).
So sánh \(d\) và \(BC.\)

Kẻ \(BH \bot AM;\,CK \bot AM\) \(\left( {H,K \in AM} \right)\).
Theo đề bài ta có \(d = BH + CK\)
+ Trường hợp 1: Nếu \(AM\) không vuông góc với \(BC\) khi đó:
\(BH,\,BM\) lần lượt là đường vuông góc và đường xiên kẻ từ \(B\) đến \(AM\) suy ra \(BM > BH\) (1)
\(CK,\,CM\) lần lượt là đường vuông góc và đường xiên kẻ từ \(C\) đến \(AM\) suy ra \(CM > CK\) (2)
Cộng (1) với (2) theo vế với vế ta được:
\(BM + CM > BH + CK\) hay \(BC > d.\)
+ Trường hợp 2: Nếu \(AM\, \bot \,BC\)khi đó \(H,\,M,\,K\) trùng nhau.
Tam giác \(ABC\) có hai góc \(B,C\) nhọn nên \(M\) nằm giữa hai điểm \(B\) và \(C\) do đó \(BH + CK = BM + CM\) hay \(BC = d\).
Vậy \(d \le BC\).
Chọn câu đúng.
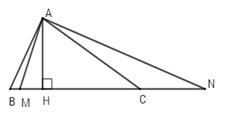
Vì $M$ nằm giữa $B$ và $H$ \( \Rightarrow HM < HB\) .
Mà $HM$ và $HB$ tương ứng là hình chiếu của $AM$ và $AB$ trên $BC$
$ \Rightarrow AM < AB\left( 2 \right)$ (quan hệ giữa đường xiên và hình chiếu).
Vì $N$ thuộc tia đối của tia $CB$ thì suy ra \(HN > HC\). Mà $HN$ và $HC$ tương ứng là hình chiếu của $AN$ và $AC$ trên $BC$ \( \Rightarrow AC < AN\left( 3 \right)\) (quan hệ giữa đường xiên và hình chiếu).
Từ \(\left( 1 \right)\left( 2 \right)\left( 3 \right) \Rightarrow AM < AB < AN.\)
So sánh \(HB\) và \(HC.\)
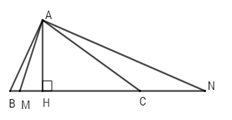
Vì \(\widehat B > \widehat C\left( {gt} \right) \)\(\Rightarrow AC > AB\left( 1 \right)\) (quan hệ giữa góc và cạnh trong tam giác).
Mà $HB, HC$ tương ứng là hình chiếu của $AB, AC$ trên $BC$
\( \Rightarrow HB < HC\) (quan hệ giữa đường xiên và hình chiếu).
So sánh \(HB\) và \(HC.\)

Vì \(\widehat B > \widehat C\left( {gt} \right) \)\(\Rightarrow AC > AB\left( 1 \right)\) (quan hệ giữa góc và cạnh trong tam giác).
Mà $HB, HC$ tương ứng là hình chiếu của $AB, AC$ trên $BC$
\( \Rightarrow HB < HC\) (quan hệ giữa đường xiên và hình chiếu).
So sánh \(HB\) và \(HC.\)

Vì \(\widehat B > \widehat C\left( {gt} \right) \)\(\Rightarrow AC > AB\left( 1 \right)\) (quan hệ giữa góc và cạnh trong tam giác).
Mà $HB, HC$ tương ứng là hình chiếu của $AB, AC$ trên $BC$
\( \Rightarrow HB < HC\) (quan hệ giữa đường xiên và hình chiếu).
Em hãy chọn phát biểu sai trong các phát biểu sau:
Trong các phát biểu ở ý A, B, và D đều đúng. Ý C sai vì: trong hai đường xiên kẻ từ một điểm nằm ngoài một đường thẳng đến đường thẳng đó thì đường xiên nào lớn hơn thì có hình chiếu lớn hơn.
Cho ba điểm \(A,\,B,\,C\) thẳng hàng, \(B\) nằm giữa \(A\) và \(C\). Trên đường thẳng vuông góc với \(AC\) tại \(B\) ta lấy điểm \(H\). Khi đó
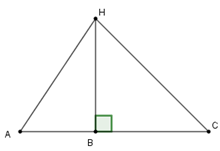
Vì \(BH\) là đường vuông góc và \(AH\) là đường xiên nên \(AH > BH.\)
Trong tam giác \(ABC\) có chiều cao \(AH\)
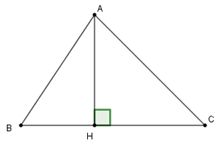
Trong tam giác \(ABC\) có \(AH\) là đường vuông góc và \(BH;CH\) là hai hình chiếu
Khi đó
+ Nếu \(AB < AC\) thì \(BH < HC\)
+ Nếu \(BH < HC\) thì \(AB < AC\)
+ Nếu \(BH = HC\) thì \(AB = AC\)
Nên cả A, B, C đều đúng.
Cho hình vẽ sau:
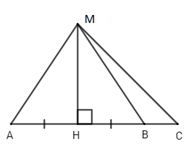
Em hãy chọn đáp án sai trong các đáp án sau:
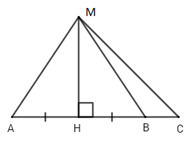
Vì $MH$ là đường vuông góc và $MA$ là đường xiên nên \(MA > MH\) (quan hệ đường vuông góc và đường xiên). Đáp án A đúng nên loại A.
Vì \(\widehat {MBC}\) là góc ngoài của \(\Delta MHB \Rightarrow \widehat {MBC} > \widehat {MHB} = {90^0}\)
Xét \(\Delta MBC\) có: \(\widehat {MBC}\) là góc tù nên suy ra \(MC > MB\) (quan hệ giữa góc và cạnh trong tam giác)
Mà $HB$ và $HC$ lần lượt là hình chiếu của $MB$ và $MC$ trên $AC.$
\( \Rightarrow HB < HC\) (quan hệ giữa đường xiên và hình chiếu). Đáp án B đúng nên loại đáp án B.
Vì \(AH = HB\left( {gt} \right)\) mà $AH$ và $HB$ lần lượt là hai hình chiếu của $AM$ và $BM.$
\( \Rightarrow MA = MB\) (quan hệ giữa đường xiên và hình chiếu). Đáp án C đúng nên loại đáp án C.
Ta có: \(\left\{ \begin{array}{l}MB = MA\left( {cmt} \right)\\MC > MB\left( {cmt} \right)\end{array} \right. \Rightarrow MC > MA\). Đáp án D sai nên chọn đáp án D.
Cho \(\Delta ABC\) vuông tại $A,M$ là trung điểm của $AC.$ Gọi $D,E$ lần lượt là hình chiếu của $A$ và $C$ xuống đường thẳng $BM.$ So sánh \(BD + BE\) và $AB.$
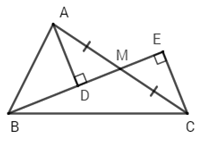
Vì \(\Delta ABM\) vuông tại $A$ (gt) nên \(BA < BM\) (quan hệ giữa đường vuông góc và đường xiên).
Mà \(BM = BD + DM \Rightarrow BA < BD + DM\left( 1 \right)\) .
Mặt khác, \(BM = BE - ME \Rightarrow BA < BE - ME\left( 2 \right)\)
Cộng hai vế của \(\left( 1 \right)\)và \(\left( 2 \right)\) ta được: \(2BA < BD + BE + MD - ME\left( 3 \right)\)
Vì $M$ là trung điểm của $AC$ (gt) \( \Rightarrow AM = MC\) (tính chất trung điểm)
Xét tam giác vuông $ADM$ và tam giác vuông $CEM$ có:
\(AM = MC\left( {cmt} \right)\)
\(\widehat {AMD} = \widehat {EMC}\) (đối đỉnh)
\( \Rightarrow \Delta ADM = \Delta CEM\) (cạnh huyền – góc nhọn)
\( \Rightarrow MD = ME\left( 4 \right)\) (2 cạnh tương ứng)
Từ \(\left( 3 \right)\)và \(\left( 4 \right) \Rightarrow BD + BE > 2AB\)
Cho \(\Delta ABC\) có $CE$ và $BD$ là hai đường cao. So sánh \(BD + CE\) và \(AB + AC\) ?
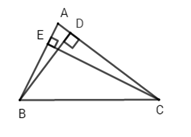
Vì \(\left\{ \begin{array}{l}BD \bot AC\left( {gt} \right)\\EC \bot AB\left( {gt} \right)\end{array} \right. \Rightarrow \)$BD$ và $CE$ là lần lượt là hai đường vuông góc của hai đường xiên $AC$ và $AB.$
\( \Rightarrow \left\{ \begin{array}{l}BD < AB\\EC < AC\end{array} \right.\) (đường vuông góc nhỏ hơn đường xiên)
\( \Rightarrow BD + EC < AB + AC\)

