Bài tập ôn tập chương 3: Thống kê

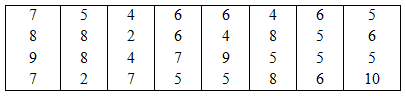
Dấu hiệu điều tra là điểm bài kiểm tra môn Toán học kì I của mỗi học sinh lớp 7A.

Có tất cả $32$  giá trị của dấu hiệu.

Có 8 giá trị khác nhau của dấu hiệu, đó là $2;{\rm{ }}4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7;{\rm{ }}8;{\rm{ }}9;{\rm{ }}10.$

Từ bảng số liệu ban đầu ta lập được bảng “tần số” như sau:

Từ bảng “tần số” ta thấy giá trị $5$  điểm có tần số lớn nhất. Vậy ${M_0} = {\rm{ }}5.$

Bảng tần số  (theo câu trước)

Quan sát bảng tần số ta có tần số của điểm 8 là 5.

Từ bảng tần số

Số trung bình cộng là :

$\overline X  = \dfrac{{2.2 + 4.4 + 5.8 + 6.6 + 7.4 + 8.5 + 9.2 + 10.1}}{{32}} = \dfrac{{192}}{{32}} = 6$ (điểm)

Bảng “tần số”

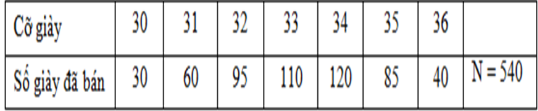
Cỡ giày “đại diện” chính là số trung bình cộng.

Vậy cỡ giày đại diện là:

$X  = \dfrac{{30.30 + 31.60 + 32.95 + 33.110 + 34.120 + 35.85 + 36.40}}{{540}} = \dfrac{{17925}}{{540}} \approx 33,19$

Bảng “tần số”

Từ bảng tần số ta thấy cỡ giày $34$  bán được nhiều nhất ($120$ đôi). Vậy mốt của dấu hiệu là : ${M_0} = {\rm{ }}34$

Cửa hàng đó bán được tất cả số đôi giày là: $30 + 60 + 95 + 110 + 120 + 85 + 40 = 540$  (đôi giày)

Cửa hàng đó bán được tất cả số đôi giày là: $30 + 60 + 95 + 110 + 120 + 85 + 40 = 540$  (đôi giày)

Có $9$  giá trị khác nhau của dấu hiệu thống kê, đó là $4;{\rm{ }}5;{\rm{ }}6;{\rm{ }}7;{\rm{ }}8;{\rm{ }}9;{\rm{ }}10;{\rm{ }}11;{\rm{ }}12.$

Ta có $y = 11$ (theo câu trước)

Theo bài ra thì số trung bình cộng của dấu hiệu là $19$ nên

$\dfrac{{15.3 + 18.11 + 22.5 + 24.7 + 9x}}{{35}} = 19$

$\begin{array}{l} \Leftrightarrow \dfrac{{521 + 9x}}{{35}} = 19\\ \Leftrightarrow 521 + 9x = 665\\ \Leftrightarrow 9x = 144\\ \Leftrightarrow x = 16\end{array}$

Vậy $x = 16.$

Số học sinh làm bài toán trong $6$  phút là $3$  bạn.

Theo bài, ta có: 
$N = 35 \Leftrightarrow 3 + y + 5 + 7 + 9 = 35 \Leftrightarrow 24 + y = 35 \Leftrightarrow y = 35 - 24 = 11$
Với $y = 11$  thì giá trị  $18$ có tần số lớn nhất là $11$ . 
Do đó, mốt của dấu hiệu là ${M_0} = 18.$

Số trung bình cộng là:

$\overline X  = \dfrac{{4.6 + 5.4 + 6.3 + 7.2 + 8.8 + 9.5 + 10.4 + 11.3 + 12.1}}{{36}} = \dfrac{{270}}{{36}} = 7,5\,$(phút).

Theo bài, ta có: 
$N = 35 \Leftrightarrow 3 + y + 5 + 7 + 9 = 35 \Leftrightarrow 24 + y = 35 \Leftrightarrow y = 35 - 24 = 11$
Với $y = 11$  thì giá trị  $18$ có tần số lớn nhất là $11$ . 
Do đó, mốt của dấu hiệu là ${M_0} = 18.$

Số học sinh làm bài toán trong 8 phút chiếm tỉ lệ cao nhất (tần số là 8). Vậy mốt là M₀ = 8.

Từ bảng tần số

Số trung bình cộng là :

$\overline X  = \dfrac{{2.2 + 4.4 + 5.8 + 6.6 + 7.4 + 8.5 + 9.2 + 10.1}}{{32}} = \dfrac{{192}}{{32}} = 6$ (điểm)

Bảng tần số  (theo câu trước)

Quan sát bảng tần số ta có tần số của điểm 8 là 5.

Từ bảng số liệu ban đầu ta lập được bảng “tần số” như sau:

Từ bảng “tần số” ta thấy giá trị $5$  điểm có tần số lớn nhất. Vậy ${M_0} = {\rm{ }}5.$