Số nguyên \(x\) thoả mãn điều kiện \(\dfrac{{ - 42}}{7} < x < \dfrac{{ - 24}}{6}\) là:
\(\begin{array}{l}\dfrac{{ - 42}}{7} < x < \dfrac{{ - 24}}{6}\\ \Rightarrow - 6 < x < - 4\end{array}\)
Mà \(x\in \mathbb Z\) nên \( x = - 5\).
Hỗn số \( - 3\dfrac{2}{5}\) viết dưới dạng phân số là:
\( - 3\dfrac{2}{5} = - \dfrac{{3.5 + 2}}{5} = - \dfrac{{17}}{5}\)
Cho biết \(\dfrac{{x + 1}}{4} = \dfrac{{ - 9}}{{12}}\), khi đó giá trị của \(x\) là:
\(\begin{array}{l}
\dfrac{{x + 1}}{4} = \dfrac{{ - 9}}{{12}}\\
\Rightarrow \dfrac{{x + 1}}{4} = \dfrac{{ - 3}}{4}\\
\Rightarrow x + 1 = - 3\\
\Rightarrow x = - 3 - 1 = - 4
\end{array}\)
Vậy giá trị của \(x\) là \( - 4.\)
Số đối của \(\dfrac{{ - 3}}{7}\) là:
\(\dfrac{{ - 3}}{7} + \dfrac{3}{7} = \dfrac{{\left( { - 3} \right) + 3}}{7} = 0\)
Biết \(\dfrac{2}{7}\) của \(a\) bằng \(28\), số \(a\) là:
\(a = 28:\dfrac{2}{7} = 28.\dfrac{7}{2} = 98\)
Cho góc \(xOy\) và góc \({zOt}\) là hai góc bù nhau. Nếu góc \(xOy\) bằng \({50^o}\) thì số đo góc \(zOt\) là:
Vì \(\widehat {xOy}\) và \(\widehat {zOt}\) là hai góc bù nhau nên ta có:
\(\begin{array}{l}\widehat {xOy} + \widehat {zOt} = {180^o}\\ \Rightarrow \widehat {zOt} = {180^o} - \widehat {xOy} = {180^o} - {50^o} = {130^o}.\end{array}\)
Hình gồm các điểm cách \(O\) một khoảng \(6cm\) là:
Hình gồm các điểm cách \(O\) một khoảng \(6cm\) là đường tròn tâm \(O\), bán kính \(6cm.\)
Kết quả của biểu thức \(A = \dfrac{{ - 3}}{{13}} - \dfrac{7}{{17}} + \dfrac{{ - 5}}{{19}} + \dfrac{{ - 10}}{{13}} + \dfrac{{24}}{{17}} - \dfrac{{14}}{{19}}\) là:
\(\begin{array}{l}A = \dfrac{{ - 3}}{{13}} - \dfrac{7}{{17}} + \dfrac{{ - 5}}{{19}} + \dfrac{{ - 10}}{{13}} + \dfrac{{24}}{{17}} - \dfrac{{14}}{{19}}\\\,\,\,\,\,\, = \left( {\dfrac{{ - 3}}{{13}} + \dfrac{{ - 10}}{{13}}} \right) + \left( { - \dfrac{7}{{17}} + \dfrac{{24}}{{17}}} \right) + \left( {\dfrac{{ - 5}}{{19}} + \dfrac{{ - 14}}{{19}}} \right)\\\,\,\,\,\,\, = \dfrac{{ - 13}}{{13}} + \dfrac{{17}}{{17}} + \dfrac{{ - 19}}{{19}} = \left( { - 1} \right) + 1 + \left( { - 1} \right) = - 1\end{array}\)
Giá trị của biểu thức \(\dfrac{7}{5}.\dfrac{4}{9} + \dfrac{7}{5}:\dfrac{9}{{16}} - \dfrac{{14}}{{10}}.\dfrac{2}{9}\) là:
\(\begin{array}{l}\dfrac{7}{5}.\dfrac{4}{9} + \dfrac{7}{5}:\dfrac{9}{{16}} - \dfrac{{14}}{{10}}.\dfrac{2}{9}\\ = \dfrac{7}{5}.\dfrac{4}{9} + \dfrac{7}{5}.\dfrac{{16}}{9} - \dfrac{7}{5}.\dfrac{2}{9}\\ = \dfrac{7}{5}.\left( {\dfrac{4}{9} + \dfrac{{16}}{9} - \dfrac{2}{9}} \right)\\ = \dfrac{7}{5}.\dfrac{{18}}{9} = \dfrac{7}{5}.2 = \dfrac{{14}}{5}\end{array}\)
Số đo \(\widehat {xOz}\) là:
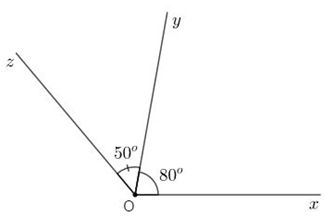
Vì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) nên ta có:
\(\begin{array}{l}\widehat {xOz} = \widehat {xOy} + \widehat {yOz}\\ \Rightarrow \widehat {xOz} = {80^o} + {50^o} = {130^o}\end{array}\)
Số đo \(\widehat {xOz}\) là:

Vì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) nên ta có:
\(\begin{array}{l}\widehat {xOz} = \widehat {xOy} + \widehat {yOz}\\ \Rightarrow \widehat {xOz} = {80^o} + {50^o} = {130^o}\end{array}\)
Vẽ tia \(Om\) là tia phân giác của \(\widehat {xOy}\) . Số đo \(\widehat {mOz}\) là:
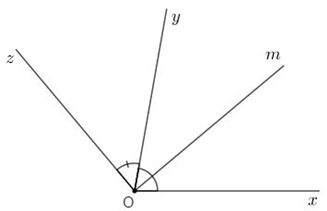
Vì \(Om\) là phân giác của \(\widehat {xOy}\) nên \(Om\) nằm giữa hai tia \(Ox\), \(Oy\) và \(\widehat {xOm} = \widehat {mOy} = \dfrac{1}{2}\widehat {xOy} = \dfrac{1}{2}{.80^o} = {40^o}\)
Ta có \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\), \(Om\) nằm giữa hai tia \(Ox\) và \(Oy\) nên \(Oy\) nằm giữa hai tia \(Om\) và \(Oz\).
Do đó: \(\widehat {mOz} = \widehat {mOy} + \widehat {yOz}\)
\( \Rightarrow \widehat {mOz} = {40^o} + {50^o} = {90^o}.\)
Với \(n \in\mathbb Z\) để \(A = \dfrac{{n - 1}}{{n - 2}}\left( {n \ne 2} \right)\) có giá trị nguyên thì \(n\) nhận những giá trị là:
Ta có: \(A = \dfrac{{n - 1}}{{n - 2}} = \dfrac{{n - 2 + 1}}{{n - 2}} = 1 + \dfrac{1}{{n - 2}}\)
Vì \(n \in \mathbb Z\) nên để \(A\) nhận giá trị nguyên thì \(\dfrac{1}{{n - 2}}\) phải nguyên hay \(n - 2\) là ước của \(1.\)
\(Ư(1) = {\rm{\{ }}1; - 1\} \)
- Với \(n - 2 = 1 \) thì \( n = 1 + 2 = 3\)
- Với \(n - 2 = - 1 \) thì \( n = - 1 + 2 = 1\)
Vậy \(n\) nhận các giá trị là \(3\) và \(1.\)
Các giá trị \(x\) thỏa mãn \(\dfrac{3}{5} - \left| {x - \dfrac{1}{2}} \right| = 25\% \) là:
\(\begin{array}{l}\dfrac{3}{5} - \left| {x - \dfrac{1}{2}} \right| = 25\% \\\dfrac{3}{5} - \left| {x - \dfrac{1}{2}} \right| = \dfrac{{25}}{{100}}\\\dfrac{3}{5} - \left| {x - \dfrac{1}{2}} \right| = \dfrac{1}{4}\\\left| {x - \dfrac{1}{2}} \right| = \dfrac{3}{5} - \dfrac{1}{4}\\\left| {x - \dfrac{1}{2}} \right| = \dfrac{{12}}{{20}} - \dfrac{5}{{20}}\\\left| {x - \dfrac{1}{2}} \right| = \dfrac{7}{{20}}\end{array}\)
TH1:
\(\begin{array}{l}x - \dfrac{1}{2} = \dfrac{7}{{20}}\\x = \dfrac{7}{{20}} + \dfrac{1}{2}\\x = \dfrac{7}{{20}} + \dfrac{{10}}{{20}}\\x = \dfrac{{17}}{{20}}\end{array}\)
TH2:
\(\begin{array}{l}x - \dfrac{1}{2} = \dfrac{{ - 7}}{{20}}\\x = \dfrac{{ - 7}}{{20}} + \dfrac{1}{2}\\x = \dfrac{{ - 7}}{{20}} + \dfrac{{10}}{{20}}\\x = \dfrac{3}{{20}}\end{array}\)
Vậy \(x = \dfrac{{17}}{{20}}\) và \(x = \dfrac{3}{{20}}\).
Giá trị của biểu thức \(A = 1\dfrac{5}{{15}}.0,75 - \left( {\dfrac{{11}}{{20}} + 25\% } \right):\dfrac{3}{5}\) là:
\(\begin{array}{l}A = 1\dfrac{5}{{15}}.0,75 - \left( {\dfrac{{11}}{{20}} + 25\% } \right):\dfrac{3}{5}\\\,\,\,\,\,\, = \dfrac{{20}}{{15}}.\dfrac{{75}}{{100}} - \left( {\dfrac{{11}}{{20}} + \dfrac{{25}}{{100}}} \right):\dfrac{3}{5}\\\,\,\,\,\,\, = \dfrac{4}{3}.\dfrac{3}{4} - \left( {\dfrac{{11}}{{20}} + \dfrac{5}{{20}}} \right):\dfrac{3}{5}\\\,\,\,\,\,\, = 1 - \dfrac{{16}}{{20}}:\dfrac{3}{5}\, = 1 - \dfrac{4}{5}.\dfrac{5}{3}\\\,\,\,\,\,\,\, = 1 - \dfrac{4}{3} = \dfrac{3}{3} - \dfrac{4}{3} = \dfrac{{ - 1}}{3}\end{array}\)
Giá trị của \(x\) trong biểu thức \(\left( {x - 1} \right):\dfrac{4}{3} + \dfrac{9}{{16}} = \dfrac{{{{\left( { - 5} \right)}^2}}}{{{4^2}}}\) là:
\(\begin{array}{l}\left( {x - 1} \right):\dfrac{4}{3} + \dfrac{9}{{16}} = \dfrac{{{{\left( { - 5} \right)}^2}}}{{{4^2}}}\\\left( {x - 1} \right):\dfrac{4}{3} + \dfrac{9}{{16}} = \dfrac{{25}}{{16}}\\\left( {x - 1} \right):\dfrac{4}{3} = \dfrac{{25}}{{16}} - \dfrac{9}{{16}}\\\left( {x - 1} \right):\dfrac{4}{3} = \dfrac{{16}}{{16}}\\\left( {x - 1} \right):\dfrac{4}{3} = 1\\x - 1 = 1.\dfrac{4}{3}\\x - 1 = \dfrac{4}{3}\\x = \dfrac{4}{3} + 1\\x = \dfrac{4}{3} + \dfrac{3}{3}\\x = \dfrac{7}{3}\end{array}\)
Học kì I lớp 6A có \(20\) học sinh giỏi. Học kì II số học sinh giỏi tăng thêm \(20\% \) . Số học sinh giỏi của lớp 6A trong học kì II là:
Số học sinh giỏi tăng thêm trong học kì II của lớp 6A là:
\(20.20\% = 20.\dfrac{{20}}{{100}} = 4\) (học sinh)
Số học sinh giỏi của lớp 6A trong học kì II là:
\(20 + 4 = 24\) (học sinh)
Trong một đợt lao động trồng cây, lớp 6A gồm ba tổ được phân công trồng \(250\) cây. Biết rằng cây tổ I trồng được bằng \(\dfrac{2}{5}\) tổng số cây cả lớp trồng và \(30\% \) số cây tổ II trồng được bằng \(24\) cây. Tỉ số phần trăm của số cây trồng được của tổ III so với số cây của cả lớp trồng là:
Tổ I trồng được số cây là: \(\dfrac{2}{5}.250 = 100\) (cây)
Tổ II trồng được số cây là: \(24:30\% = 24:\dfrac{{30}}{{100}} = 80\) (cây)
Tổ III trồng được số cây là: \(250 - 100 - 80 = 70\) (cây)
Tỉ số phần trăm của số cây trồng được của tổ III so với số cây của cả lớp trồng là:
\(\dfrac{{70}}{{250}}.100\% = 28\% \)
Cho \(\widehat {xOy} = {80^0},\widehat {yOz} = {50^0}\) , tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\).
Số đo \(\widehat {xOz}\) là:

Vì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) nên ta có:
\(\begin{array}{l}\widehat {xOz} = \widehat {xOy} + \widehat {yOz}\\ \Rightarrow \widehat {xOz} = {80^o} + {50^o} = {130^o}\end{array}\)
Cho \(\widehat {xOy} = {80^0},\widehat {yOz} = {50^0}\) , tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\).
Vẽ tia \(Om\) là tia phân giác của \(\widehat {xOy}\) . Số đo \(\widehat {mOz}\) là:

Vì \(Om\) là phân giác của \(\widehat {xOy}\) nên \(Om\) nằm giữa hai tia \(Ox\), \(Oy\) và \(\widehat {xOm} = \widehat {mOy} = \dfrac{1}{2}\widehat {xOy} = \dfrac{1}{2}{.80^o} = {40^o}\)
Ta có \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\), \(Om\) nằm giữa hai tia \(Ox\) và \(Oy\) nên \(Oy\) nằm giữa hai tia \(Om\) và \(Oz\).
Do đó: \(\widehat {mOz} = \widehat {mOy} + \widehat {yOz}\)
\( \Rightarrow \widehat {mOz} = {40^o} + {50^o} = {90^o}.\)

