\(\dfrac{3}{4}\) của \(60\) là:
\(\dfrac{3}{4}\) của \(60\) là: \(\dfrac{3}{4} \times 60 = 45\).
Số đối của \(\dfrac{{ - 7}}{{13}}\) là:
Số đối của \(\dfrac{A}{B}\) là \(\dfrac{{ - A}}{B}\).
Do đó số đối của \(\dfrac{{ - 7}}{{13}}\) là: \(\dfrac{7}{{13}}\)
Kết quả phép tính \(12 + \left( { - 22} \right)\) là:
Ta có : \(12 + \left( { - 22} \right) = - \left( {22 - 12} \right) = - 10\)
Tổng các phần tử của tập hợp \(A = \left\{ {x \in \mathbb{Z}| - 5 \le x \le 5} \right\}\) là:
Ta liệt kê các phần tử của A rồi cộng chúng lại.
\(A = \left\{ { - 5; - 4; - 3; - 2; - 1;0;1;2;3;4;5} \right\}\)
Tổng là:
\(S = - 5 + \left( { - 4} \right) + \left( { - 3} \right) + \left( { - 2} \right) + \left( { - 1} \right)\)\(\, + 0 + 1 + 2 + 3 + 4 + 5\)
\(= \left( {5 - 5} \right) + \left( {4 - 4} \right) + \left( {3 - 3} \right) \)\(\,+ \left( {2 - 2} \right) + \left( {1 - 1} \right) + 0\)
\(= 0\)
Số đo của góc bẹt là:
Góc bẹt là góc có số đo bằng \({180^0}\).
Tổng của hai phân số \(\dfrac{3}{4}\) và \(\dfrac{{ - 5}}{2}\) là:
Ta có : \(\dfrac{3}{4} + \left( {\dfrac{{ - 5}}{2}} \right) = \dfrac{3}{4} + \left( {\dfrac{{ - 10}}{4}} \right) = \dfrac{{3 + \left( { - 10} \right)}}{4} = \dfrac{{ - 7}}{4}\)
Thương trong phép chia \(\dfrac{{ - 5}}{7}:\dfrac{7}{5}\) là:
Ta có : \(\dfrac{{ - 5}}{7}:\dfrac{7}{5} = \dfrac{{ - 5}}{7}.\dfrac{5}{7} = \dfrac{{ - 25}}{{49}}\)
Cho các khẳng định sau:
(1) Hình tròn là tập hợp các điểm nằm trên đường tròn và những điểm nằm trong đường tròn.
(2) Trong một đường tròn, đường kính là dây lớn nhất.
(3) Trong một đường tròn, đường kính gấp ba lần bán kính.
Số khẳng định đúng là:
- Hình tròn là tập hợp các điểm nằm trên đường tròn và những điểm nằm trong đường tròn \( \Rightarrow \) Khẳng định (1) đúng.
- Dây cung đi qua tâm là đường kính là dây cung lớn nhất \( \Rightarrow \) Khẳng định (2) đúng.
- Đường kính gấp hai lần bán kính \( \Rightarrow \) Khẳng định (3) sai.
Vậy số khẳng định đúng là \(2.\)
Cho các khẳng định sau:
(1) Góc là hình gồm hai tia chung gốc.
(2) Góc nhọn có số đo lớn hơn \(0^0\) và nhỏ hơn \({90^o}.\)
(3) Hai góc bù nhau có tổng số đo bằng \({90^o}.\)
(4) Số đo mỗi góc không vượt quá \({180^o}.\)
Số khẳng định đúng là:
- Góc là hình gồm hai tia chung gốc \( \Rightarrow \) Khẳng định (1) đúng.
- Góc nhọn có số đo lớn hơn \(0^0\) và nhỏ hơn \({90^o}\)\( \Rightarrow \) Khẳng định (2) đúng.
- Hai góc bù nhau có tổng số đo bằng \({180^o}\) \( \Rightarrow \) Khẳng định (3) sai.
- Số đo mỗi góc không vượt quá \({180^o}\)\( \Rightarrow \) Khẳng định (4) đúng.
Vậy có \(3\) khẳng định đúng.
Vẽ tia \(Oa'\) là tia đối của tia \(Oa\) . Số đo \(\widehat {bOa'}\) là:

Vì \(Oa'\) là tia đối của tia \(Oa\) nên \(\widehat {aOb}\) và \(\widehat {bOa'}\) là hai góc kề bù, ta có:
\(\begin{array}{l}\widehat {aOb} + \widehat {bOa'} = \widehat {aOa'}\\ \Rightarrow {50^0} + \,\,\,\widehat {\,bOa'} = {180^0}\\ \Rightarrow \widehat {bOa'} = {180^0} - {50^0} = {130^0}\end{array}\)
Số đo \(\widehat {bOc}\) là:
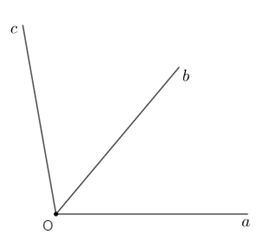
Trên nửa mặt phẳng bờ chứa tia \(Oa\) có \(\widehat {aOb} < \widehat {aOc}\,\,\left( {{{50}^0} < {{100}^o}} \right)\) nên tia \(Ob\) nằm giữa hai tia \(Oa;\,Oc\)
\(\begin{array}{l} \Rightarrow \widehat {aOb} + \widehat {bOc} = \widehat {aOc}\\ \Rightarrow {50^0}\,\, + \,\widehat {bOc} = {100^0}\\ \Rightarrow \,\,\widehat {bOc} = {100^0} - {50^0} = {50^0}\end{array}\)
Số đo \(\widehat {bOc}\) là:

Trên nửa mặt phẳng bờ chứa tia \(Oa\) có \(\widehat {aOb} < \widehat {aOc}\,\,\left( {{{50}^0} < {{100}^o}} \right)\) nên tia \(Ob\) nằm giữa hai tia \(Oa;\,Oc\)
\(\begin{array}{l} \Rightarrow \widehat {aOb} + \widehat {bOc} = \widehat {aOc}\\ \Rightarrow {50^0}\,\, + \,\widehat {bOc} = {100^0}\\ \Rightarrow \,\,\widehat {bOc} = {100^0} - {50^0} = {50^0}\end{array}\)
Vẽ tia \(Oa'\) là tia đối của tia \(Oa\), đường tròn \(\left( {O;2cm} \right)\) cắt tia \(Oa\) tại điểm \(M\), cắt tia \(Oa'\) tại \(N\). Trên tia \(Oa\) lấy điểm \(P\) sao cho \(OP = 5cm.\) Độ dài đoạn thẳng \(MP\) là:

\(M \in Oa;\,N \in Oa'\)
Trên tia \(Oa\) có \(OM < OP\,\left( {2cm < 5cm} \right)\) nên \(M\) nằm giữa \(O\) và \(P\).
\(\begin{array}{l} \Rightarrow OM + MP = OP\\ \Rightarrow 2\,\,\,\,\,\,\,\, + MP = 5\\ \Rightarrow MP = 5 - 2 = 3\left( {cm} \right)\end{array}\)
Biết \(\widehat A,\,\widehat B\) phụ nhau và \(\widehat A - \widehat B = {10^o}\). Số đo góc \(\widehat A,\,\widehat B\) lần lượt là:
\(\widehat A - \widehat B = {10^o} \Rightarrow \widehat A = \widehat B + {10^o}\,\,\,\,\,\,\,(\,1\,)\)
Vì \(\widehat A \) và \( \widehat B\) phụ nhau nên ta có:
\(\widehat A + \widehat B = {90^o}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(2)\)
Thay (1) và (2) ta được:
\(\begin{array}{l}\widehat B + {10^o} + \widehat B = {90^o}\\ \Rightarrow 2\widehat B + {10^o} = {90^o}\\ \Rightarrow 2\widehat B = {90^o} - {10^o}\\ \Rightarrow 2\widehat B = {80^o}\\ \Rightarrow \widehat B = {80^o}:2 = {40^o}\\ \Rightarrow \widehat A = {40^o} + {10^o} = {50^o}.\end{array}\)
Biết \(\dfrac{1}{3} + 2 + \dfrac{2}{3} < x < \dfrac{{ - 17}}{{13}} + 6 + \dfrac{4}{{13}}\,\,\left( {x \in \mathbb{Z}} \right)\). Số nguyên \(x\) là:
\(\dfrac{1}{3} + 2 + \dfrac{2}{3} = \left( {\dfrac{1}{3} + \dfrac{2}{3}} \right) + 2 = \dfrac{3}{3} + 2\)\(\, = 1 + 2 = 3\)
\(\dfrac{{ - 17}}{{13}} + 6 + \dfrac{4}{{13}}\, = \left( {\dfrac{{ - 17}}{{13}} + \dfrac{4}{{13}}} \right) + 6 \)\(\,= \dfrac{{ - 13}}{{13}} + 6 = \left( { - 1} \right) + 6 = 5\)
Do đó \(3 < x < 5\) và \(x \in \mathbb{Z}\) nên \(x = 4\).
Cho các chữ số \(a,b\) thỏa mãn \(a - b = 4\) và \(\overline {87ab} \,\, \vdots \,\,9\). Giá trị \(a,\,b\) là:
Để \(\overline {87ab} \,\, \vdots \,\,9\) thì \(\left( {8 + 7 + a + b} \right)\, \vdots \,\,9\) hay \(\left( {15 + a + b} \right)\, \vdots \,\,9\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
Theo đề bài \(a - b = 4 \Rightarrow a = b + 4\,\,\,\,\,\,\,\,\,\,(2)\)
Thay (2) vào (1) ta được:
\(\begin{array}{l}\left( {15 + b + 4 + b} \right)\, \vdots \,\,9\\ \Rightarrow \left( {19 + 2b} \right)\,\, \vdots \,\,9\end{array}\)
Mà \(b \in {\rm{\{ }}0;1;2;3;4;5;6;7;8;9\} \)
Do đó \(b = 4 \Rightarrow a = 4 + 4 = 8.\)
Vậy \(a = 8;b = 4\).
Kết quả của phép tính: \(| - 7| + \left( { - 12} \right)\) là:
\(| - 7| + \left( { - 12} \right) = 7 + \left( { - 12} \right) \)\(\,= - \left( {12 - 7} \right) = - 5\)
Kết quả của phép tính: \(\dfrac{4}{7}.\dfrac{2}{{11}} + \dfrac{4}{7}.\dfrac{{12}}{{11}} - \dfrac{4}{7}.\dfrac{7}{{11}}\) là:
\(\begin{array}{l}\dfrac{4}{7}.\dfrac{2}{{11}} + \dfrac{4}{7}.\dfrac{{12}}{{11}} - \dfrac{4}{7}.\dfrac{7}{{11}}\\ = \dfrac{4}{7}.\left( {\dfrac{2}{{11}} + \dfrac{{12}}{{11}} - \dfrac{7}{{11}}} \right)\\ = \dfrac{4}{7}.\dfrac{7}{{11}} = \dfrac{4}{{11}}\end{array}\)
Biết \(20\% x + \dfrac{3}{5} = 15\). Giá trị của \(x\) là:
\(\begin{array}{l}20\% x + \dfrac{3}{5} = 15\\\dfrac{{20}}{{100}}.x + \dfrac{3}{5} = 15\\\dfrac{1}{5}.x = 15 - \dfrac{3}{5}\\ \dfrac{1}{5}.x = \dfrac{{75}}{5} - \dfrac{3}{5}\\\dfrac{1}{5}.x = \dfrac{{72}}{5} \\ x = \dfrac{{72}}{5}:\dfrac{1}{5}\\x = \dfrac{{72}}{5}.\dfrac{5}{1}\\x = 72\end{array}\)
Khối 6 của một trường có tổng cộng 90 học sinh trong dịp tổng kết cuối năm thống kê được: Số học sinh giỏi bằng \(\dfrac{1}{6}\) số học sinh cả khối, số học sinh khá bằng \(40\% \) số học sinh cả khối. Số học sinh trung bình bằng \(\dfrac{1}{3}\) số học sinh cả khối, còn lại là học sinh yếu. Số học sinh yếu là:
Số học sinh giỏi của trường là:
\(90.\dfrac{1}{6} = 15\) (học sinh)
Số học sinh khá của trường là:
\(90.40\% = 90.\dfrac{{40}}{{100}} = 36\) (học sinh)
Số học sinh trung bình của trường là:
\(90.\dfrac{1}{3} = 30\) (học sinh)
Số học sinh yếu của trường là: \(90 - \left( {15 + 36 + 30} \right) = 9\) (học sinh)

