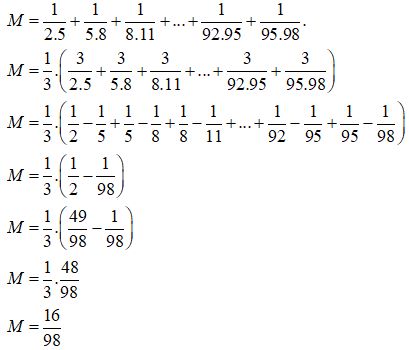Trên cùng một nửa mặt phẳng bờ chứa tia \(Oa\) , vẽ tia \(Ob\) sao cho \(\widehat {aOb} = {50^0}\) , vẽ tia \(Oc\) sao cho \(\widehat {aOc} = {100^o}\)
Số đo \(\widehat {bOc}\) là:
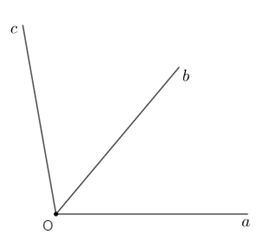
Trên nửa mặt phẳng bờ chứa tia \(Oa\) có \(\widehat {aOb} < \widehat {aOc}\,\,\left( {{{50}^0} < {{100}^o}} \right)\) nên tia \(Ob\) nằm giữa hai tia \(Oa;\,Oc\)
\(\begin{array}{l} \Rightarrow \widehat {aOb} + \widehat {bOc} = \widehat {aOc}\\ \Rightarrow {50^0}\,\, + \,\widehat {bOc} = {100^0}\\ \Rightarrow \,\,\widehat {bOc} = {100^0} - {50^0} = {50^0}\end{array}\)
Trên cùng một nửa mặt phẳng bờ chứa tia \(Oa\) , vẽ tia \(Ob\) sao cho \(\widehat {aOb} = {50^0}\) , vẽ tia \(Oc\) sao cho \(\widehat {aOc} = {100^o}\)
Vẽ tia \(Oa'\) là tia đối của tia \(Oa\) . Số đo \(\widehat {bOa'}\) là:

Vì \(Oa'\) là tia đối của tia \(Oa\) nên \(\widehat {aOb}\) và \(\widehat {bOa'}\) là hai góc kề bù, ta có:
\(\begin{array}{l}\widehat {aOb} + \widehat {bOa'} = \widehat {aOa'}\\ \Rightarrow {50^0} + \,\,\,\widehat {\,bOa'} = {180^0}\\ \Rightarrow \widehat {bOa'} = {180^0} - {50^0} = {130^0}\end{array}\)
Trên cùng một nửa mặt phẳng bờ chứa tia \(Oa\) , vẽ tia \(Ob\) sao cho \(\widehat {aOb} = {50^0}\) , vẽ tia \(Oc\) sao cho \(\widehat {aOc} = {100^o}\)
Vẽ tia \(Oa'\) là tia đối của tia \(Oa\), đường tròn \(\left( {O;2cm} \right)\) cắt tia \(Oa\) tại điểm \(M\), cắt tia \(Oa'\) tại \(N\). Trên tia \(Oa\) lấy điểm \(P\) sao cho \(OP = 5cm.\) Độ dài đoạn thẳng \(MP\) là:

\(M \in Oa;\,N \in Oa'\)
Trên tia \(Oa\) có \(OM < OP\,\left( {2cm < 5cm} \right)\) nên \(M\) nằm giữa \(O\) và \(P\).
\(\begin{array}{l} \Rightarrow OM + MP = OP\\ \Rightarrow 2\,\,\,\,\,\,\,\, + MP = 5\\ \Rightarrow MP = 5 - 2 = 3\left( {cm} \right)\end{array}\)
Cho biểu thức:
\(M = \dfrac{1}{{2.5}} + \dfrac{1}{{5.8}} + \dfrac{1}{{8.11}} + ... + \dfrac{1}{{92.95}} + \dfrac{1}{{95.98}}.\)
Giá trị của biểu thức M là: