Chọn câu đúng
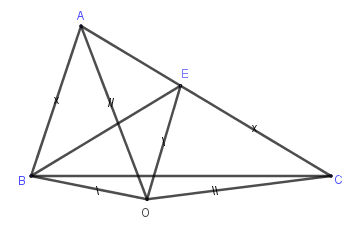
Ta có \(\Delta AOB = \Delta COE \Rightarrow \widehat {OAB} = \widehat {OCE}\,\,\left( 1 \right)\)
\(\Delta AOC\) cân tại \(O \Rightarrow \widehat {OAC} = \widehat {OCE}\,\,\left( 2 \right)\)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(\widehat {OAB} = \widehat {OAC}\) , do đó \(AO\) là tia phân giác góc \(A.\)
Chọn câu đúng.
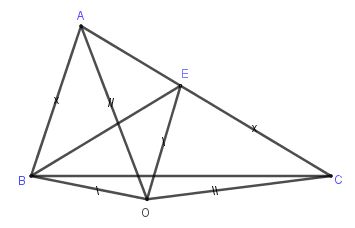
Xét tam giác \(AOB\) và \(COE\) có
+ \(OA = OC\) (vì $O$ thuộc đường trung trực của \(AC\))
+ \(OB = OE\) (vì $O$ thuộc đường trung trực của \(BE\))
+ \(AB = CE\) (giả thiết)
Do đó \(\Delta AOB = \Delta COE\left( {c - c - c} \right)\)
Chọn câu đúng.

Xét tam giác \(AOB\) và \(COE\) có
+ \(OA = OC\) (vì $O$ thuộc đường trung trực của \(AC\))
+ \(OB = OE\) (vì $O$ thuộc đường trung trực của \(BE\))
+ \(AB = CE\) (giả thiết)
Do đó \(\Delta AOB = \Delta COE\left( {c - c - c} \right)\)
Điền cụm từ thích hợp vào chỗ trống: “Ba đường trung trực của tam giác giao nhau tại một điểm. Điểm này cách đều … của tam giác đó”
Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác đó. Vậy C đúng.
Cho tam giác \(ABC\) có một đường phân giác đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là tam giác gì?

Giả sử \(\Delta ABC\) có: \(AM\) là đường phân giác đồng thời là đường trung trực ứng với cạnh \(BC\).
Vì \(AM\) là đường phân giác của \(\Delta ABC\) (gt) \( \Rightarrow \widehat {BAM} = \widehat {MAC}\) (tính chất tia phân giác)
Vì \(AM\) là đường trung trực của \(BC\) nên \(AM \bot BC \Rightarrow \widehat {AMB} = \widehat {AMC} = {90^o}\)
Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(\widehat {BAM} = \widehat {MAC}\,(cmt)\)
\(AM\) là cạnh chung
\(\widehat {AMB} = \widehat {AMC} = {90^o}\,(cmt)\)
\( \Rightarrow \Delta ABM = \Delta ACM\) (g.c.g)
\( \Rightarrow AB = AC\) (2 cạnh tương ứng) \( \Rightarrow \Delta ABC\) cân tại \(A.\)
Cho \(\Delta ABC\) cân tại \(A,\) có \(\widehat A = {50^0}\), đường trung trực của \(AB\) cắt \(BC\) ở \(D.\) Tính \(\widehat {CAD}\).

Vì \(\Delta ABC\) cân tại A (gt) \( \Rightarrow \widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
Xét \(\Delta ABC\) có: \(\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\) (định lí tổng ba góc của tam giác)
Mà \(\widehat {ABC} = \widehat {ACB}\) (cmt) nên \(\widehat {BAC} + 2\widehat {ABC} = {180^o} \Rightarrow \widehat {ABC} = \dfrac{{{{180}^o} - \widehat {BAC}}}{2} = \dfrac{{{{180}^o} - {{50}^o}}}{2} = {65^o}\)
Vì \(D\) thuộc đường trung trực của \(AB\) nên
\( \Rightarrow AD = BD\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ABD\) cân tại \(D\) (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat {DAB} = \widehat {ABC} = {65^o}\) (tính chất tam giác cân)
Mà \(\widehat {DAC} + \widehat {CAB} = \widehat {DAB} \Rightarrow \widehat {DAC} = \widehat {DAB} - \widehat {CAB} = {65^0} - {50^0} = {15^0}.\)
Cho \(\Delta ABC\) có: \(\widehat A = {35^0}.\) Đường trung trực của \(AC\) cắt \(AB\) ở \(D.\) Biết \(CD\) là tia phân giác của \(\widehat {ACB}\). Tính các góc \(\widehat {ABC};\,\widehat {ACB}\).

Vì đường trung trực của \(AC\) cắt \(AB\) tại \(D\) nên \(DA = DC\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ADC\) là tam giác cân tại \(D\) (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat A = \widehat {{C_2}}\,\left( 1 \right)\) (tính chất tam giác cân).
Vì \(CD\) là tia phân giác của \(\widehat {ACB}\) \( \Rightarrow \widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat {ACB}}}{2}\left( 2 \right)\) (tính chất tia phân giác).
Từ (1) và (2) \( \Rightarrow \widehat {ACB} = 2\widehat {{C_2}} = 2\widehat A\) mà \(\widehat A = {35^0}\) nên \(\widehat {ACB} = {2.35^o} = {70^o}\)
Xét \(\Delta ABC\) có: \(\widehat A + \widehat {ABC} + \widehat {ACB} = {180^0}\) (định lí tổng ba góc của tam giác)
\( \Rightarrow \widehat {ABC} = {180^0} - (\widehat A + \widehat {ACB}) = {180^0} - ({35^0} + {70^0}) = {75^0}\)
Vậy \(\widehat {ABC} = {75^o};\widehat {ACB} = {70^o}\).
Cho góc nhọn \(\widehat {xOy},\) trên tia \(Ox\) lấy điểm \(A;\) trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA = OB.\) Đường trung trực của \(OA\) và đường trung trực của \(OB\) cắt nhau tại \(I.\) Khi đó:
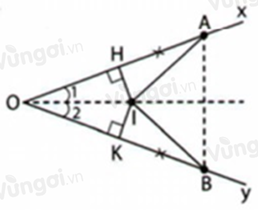
Giả sử đường trung trực của \(OA\) cắt \(OA\) tại \(H\); đường trung trực của \(OB\) cắt \(OB\) tại \(K\).
Vì \(HI\) là đường trung trực của \(OA\) nên \(IO = IA\) (tính chất đường trung trực của đoạn thẳng)
Vì \(KI\) là đường trung trực của \(OB\) nên \(IO = IB\) (tính chất đường trung trực của đoạn thẳng)
Do đó \(IA = IB\,\,(= IO)\)
Xét \(\Delta OIA\) và \(\Delta OIB\) có:
\(IA = IB\) (cmt)
\(IO\) là cạnh chung
\(OA = OB\) (gt)
Do đó \(\Delta OIA = \Delta OIB\, (c.c.c) \Rightarrow \widehat {{O_1}} = \widehat {{O_2}}\) (hai góc tương ứng)
Vậy \(OI\) là tia phân giác của \(\widehat {xOy}\). Đáp án A đúng
Theo giả thiết: \(OA = OB\) suy ra \(O\) thuộc đường trung trực của đoạn thẳng \(AB\).
Theo chứng minh trên ta có \(IA = IB\) suy ra \(I\) thuộc đường trung trực của đoạn thẳng \(AB\).
Do đó \(OI\) là đường trung trực của đoạn thẳng \(AB\).
Đáp án B đúng.
Khi \(E;F\) di động thỏa mãn \(AE = CF\) thì đường trung trực của \(EF\) đi qua điểm cố định nào?

Theo câu trước ta có: \(OE = OF\) nên \(O\) nằm trên đường trung trực của đoạn thẳng \(EF\) (tính chất đường trung trực của đoạn thẳng)
Do \(\Delta ABC\) cố định nên \(O\) cũng cố định.
Vậy đường trung trực của đoạn thẳng \(EF\) luôn đi qua điểm \(O\) cố định.
So sánh \(OE\) và \(OF\).

Vì \(O\) thuộc đường trung trực của cạnh \(AB\) nên \(OA = OB\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta OAB\) cân tại \(O\) \( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\) (tính chất tam giác cân) \((1)\)
Vì \(AH\) là đường phân giác của \(\Delta ABC\) nên \(\widehat {{A_1}} = \widehat {{A_2}}\) (tính chất tia phân giác) \((2)\)
Từ \((1)\) và \((2)\) suy ra \(\widehat {{B_1}} = \widehat {{A_2}}\)
Ta có \(AC = AF + CF\) mà \(AE = CF\) (gt) nên \(AC = AF + AE\)
Mặt khác: \(AB = AC\)(gt); \(AB = AE + BE\)
Do đó \(AF = BE\)
Xét \(\Delta BOE\) và \(\Delta AOF\) có: \(BE = AF\) (cmt); \(\widehat {{B_1}} = \widehat {{A_2}}\) (cmt); \(OB = OA\) (cmt)
Do đó \(\Delta BOE = \Delta AOF\,(c.g.c)\)
Suy ra \(OE = OF\) (hai cạnh tương ứng).
So sánh \(OE\) và \(OF\).

Vì \(O\) thuộc đường trung trực của cạnh \(AB\) nên \(OA = OB\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta OAB\) cân tại \(O\) \( \Rightarrow \widehat {{A_1}} = \widehat {{B_1}}\) (tính chất tam giác cân) \((1)\)
Vì \(AH\) là đường phân giác của \(\Delta ABC\) nên \(\widehat {{A_1}} = \widehat {{A_2}}\) (tính chất tia phân giác) \((2)\)
Từ \((1)\) và \((2)\) suy ra \(\widehat {{B_1}} = \widehat {{A_2}}\)
Ta có \(AC = AF + CF\) mà \(AE = CF\) (gt) nên \(AC = AF + AE\)
Mặt khác: \(AB = AC\)(gt); \(AB = AE + BE\)
Do đó \(AF = BE\)
Xét \(\Delta BOE\) và \(\Delta AOF\) có: \(BE = AF\) (cmt); \(\widehat {{B_1}} = \widehat {{A_2}}\) (cmt); \(OB = OA\) (cmt)
Do đó \(\Delta BOE = \Delta AOF\,(c.g.c)\)
Suy ra \(OE = OF\) (hai cạnh tương ứng).
Cho tam giác \(ABC\) trong đó: \(\widehat A = 110^\circ \). Các đường trung trực của \(AB\) và \(AC\) cắt cạnh \(BC\) theo thứ tự ở \(E\) và \(F\). Tính \(\widehat {EAF}.\)

Vì \(E\) thuộc đường trung trực của \(AB\) nên \(EA = EB\) (tính chất đường trung trực của đoạn thẳng).
Khi đó \(\Delta AEB\) cân tại \(E\) (dấu hiệu nhận biết tam giác cân) \( \Rightarrow \widehat {{A_1}} = \widehat B\) (tính chất tam giác cân).
Vì \(F\) thuộc đường trung trực của \(AC\) nên \(FA = FC\) (tính chất đường trung trực của đoạn thẳng).
Khi đó \(\Delta AFC\) cân tại \(F\) (dấu hiệu nhận biết tam giác cân) \( \Rightarrow \widehat {{A_3}} = \widehat C\) (tính chất tam giác cân).
Do đó \(\widehat {{A_1}} + \widehat {{A_3}} = \widehat B + \widehat C\)
Xét \(\Delta ABC\) có: \(\widehat {BAC} + \widehat B + \widehat C = {180^0}\) (định lí tổng ba góc của một tam giác)
\( \Rightarrow \widehat B + \widehat C = {180^0} - \widehat {BAC} = {180^0} - {110^0} = {70^0}\) hay \(\widehat {{A_1}} + \widehat {{A_3}} = {70^0}\)
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} + \widehat {{A_3}} = \widehat {BAC}\) \( \Rightarrow \widehat {{A_2}} = \widehat {BAC} - (\widehat {{A_1}} + \widehat {{A_3}}) = {110^0} - {70^0} = {40^0}.\)
So sánh \(BE + CF\) và \(BC.\)
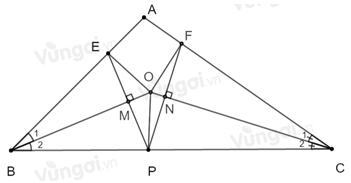
Theo câu trước ta có: \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(BE = BP\) (hai cạnh tương ứng)
Theo câu trước ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(CF = CP\) (hai cạnh tương ứng)
Khi đó \(BE + CF = BP + CP = BC\).
Chọn câu đúng.
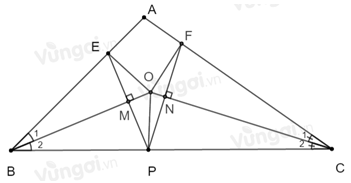
Giả sử \(EP \bot BO\) tại \(M\); \(PF \bot OC\) tại \(N\).
Khi đó \(\widehat {BME} = \widehat {BMP} = {90^0}\); \(\widehat {CNF} = \widehat {PNC} = {90^0}\)
Vì \(BO\) là tia phân giác của \(\widehat {ABC}\) (gt) nên \(\widehat {{B_1}} = \widehat {{B_2}}\) (tính chất tia phân giác)
Xét \(\Delta BME\) và \(\Delta BMP\) có:
\(\widehat {BME} = \widehat {BMP} = {90^0}\) (cmt)
\(BM\) là cạnh chung
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
Do đó \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(ME = MP\) (hai cạnh tương ứng)
Mặt khác: \(EP \bot BO\) (gt)
Vậy \(OB\) là đường trung trực của đoạn \(EP\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án A đúng.
Chứng minh tương tự ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(NF = NP\) (hai cạnh tương ứng)
Mặt khác \(PF \bot OC\) (gt)
Vậy \(OC\) là đường trung trực của đoạn \(PF\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án B đúng
Chọn câu đúng.

Giả sử \(EP \bot BO\) tại \(M\); \(PF \bot OC\) tại \(N\).
Khi đó \(\widehat {BME} = \widehat {BMP} = {90^0}\); \(\widehat {CNF} = \widehat {PNC} = {90^0}\)
Vì \(BO\) là tia phân giác của \(\widehat {ABC}\) (gt) nên \(\widehat {{B_1}} = \widehat {{B_2}}\) (tính chất tia phân giác)
Xét \(\Delta BME\) và \(\Delta BMP\) có:
\(\widehat {BME} = \widehat {BMP} = {90^0}\) (cmt)
\(BM\) là cạnh chung
\(\widehat {{B_1}} = \widehat {{B_2}}\) (cmt)
Do đó \(\Delta BME = \Delta BMP\) (g.c.g) suy ra \(ME = MP\) (hai cạnh tương ứng)
Mặt khác: \(EP \bot BO\) (gt)
Vậy \(OB\) là đường trung trực của đoạn \(EP\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án A đúng.
Chứng minh tương tự ta có: \(\Delta CNF = \Delta CNP\) (g.c.g) suy ra \(NF = NP\) (hai cạnh tương ứng)
Mặt khác \(PF \bot OC\) (gt)
Vậy \(OC\) là đường trung trực của đoạn \(PF\) (định nghĩa đường trung trực của đoạn thẳng). Đáp án B đúng
Chọn câu đúng.

Xét tam giác \(AOB\) và \(COE\) có
+ \(OA = OC\) (vì $O$ thuộc đường trung trực của \(AC\))
+ \(OB = OE\) (vì $O$ thuộc đường trung trực của \(BE\))
+ \(AB = CE\) (giả thiết)
Do đó \(\Delta AOB = \Delta COE\left( {c - c - c} \right)\)
Gọi $O$ là giao điểm của ba đường trung trực trong \(\Delta ABC\). Khi đó $O$ là:
Ba đường trung trực của một tam giác cùng đi qua 1 điểm. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác đó. Chọn đáp án D.
Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
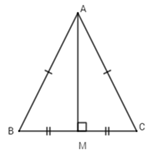
Giả sử \(\Delta ABC\) có $AM$ là trung tuyến đồng thời là đường trung trực. Ta sẽ chứng minh \(\Delta ABC\) là tam giác cân. Thật vậy, vì $AM$ là trung tuyến của \(\Delta ABC\) (gt) \( \Rightarrow BM = MC\) (tính chất trung tuyến)
Vì $AM$ là trung trực của $BC$ $ \Rightarrow AM \bot BC$
Xét hai tam giác vuông \({\Delta}ABM\) và \({\Delta}ACM\) có:
\(BM = CM\left( {cmt} \right)\)
$AM$ chung
\( \Rightarrow \Delta ABM = \Delta ACM\) (2 cạnh góc vuông)
\( \Rightarrow AB = AC\) (2 cạnh tương ứng) \( \Rightarrow \Delta ABC\) cân tại $A.$
Cho \(\Delta ABC\) cân tại $A,$ có \(\widehat A = {40^0}\), đường trung trực của $AB$ cắt $BC$ ở $D.$ Tính \(\widehat {CAD}\).
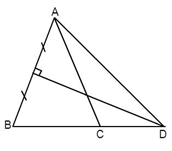
Vì \(\Delta ABC\) cân tại A (gt) \( \Rightarrow \widehat B = \widehat C = \left( {{{180}^0} - \widehat A} \right):2 = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}.\)
Vì $D$ thuộc đường trung trực của $AB$ nên
\( \Rightarrow AD = BD\) (tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ABD\) cân tại $D$ (dấu hiệu nhận biết tam giác cân)
$ \Rightarrow \widehat {DAC} + \widehat {CAB} = \widehat {DAB} = \widehat B = {70^0} \Rightarrow \widehat {DAC} = {70^0} - \widehat {CAB} = {70^0} - {40^0} = {30^0}.$
Cho \(\Delta ABC\) cân ở $A.$ Đường trung trực của $AC$ cắt $AB$ ở $D.$ Biết $CD$ là tia phân giác của \(\widehat {ACB}\) . Tính các góc của \(\Delta ABC\).
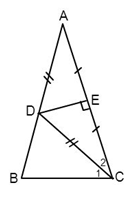
Vì đường trung trực của $AC$ cắt $AB$ tại $D$ nên suy ra \(DA = DC\)(tính chất đường trung trực của đoạn thẳng)
\( \Rightarrow \Delta ADC\) là tam giác cân tại $D$ (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat A = \widehat {{C_2}}\,\left( 1 \right)\) (tính chất tam giác cân).
Vì $CD$ là đường phân giác của \(\widehat {ACB} \Rightarrow \widehat {{C_1}} = \widehat {{C_2}} = \dfrac{{\widehat C}}{2}\left( 2 \right)\) (tính chất tia phân giác).
Từ (1) và (2) \( \Rightarrow \widehat {ACB} = 2\widehat A\).
Lại có \(\Delta ABC\) cân tại $A$ (gt) \( \Rightarrow \widehat B = \widehat {ACB}\) (tính chất tam giác cân) \( \Rightarrow \widehat B = 2\widehat A\)
Xét \(\Delta ABC\) có:
$\widehat A + \widehat B + \widehat {ACB} = {180^0} \Rightarrow \widehat A + 2\widehat A + 2\widehat A = {180^0}$
$ \Rightarrow 5\widehat A = {180^0}$$ \Rightarrow \widehat A = {36^0} \Rightarrow \widehat B = \widehat C = 2\widehat A = {2.36^0} = {72^0}$
Vậy \(\widehat A = {36^0},\widehat B = \widehat C = {72^0}.\)

