Cho góc nhọn \(\widehat {xOy},\) trên tia \(Ox\) lấy điểm \(A;\) trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA = OB.\) Đường trung trực của \(OA\) và đường trung trực của \(OB\) cắt nhau tại \(I.\) Khi đó:

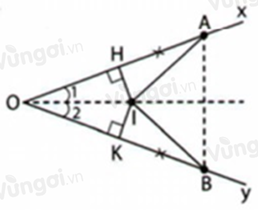
Giả sử đường trung trực của \(OA\) cắt \(OA\) tại \(H\); đường trung trực của \(OB\) cắt \(OB\) tại \(K\).

Vì \(HI\) là đường trung trực của \(OA\) nên \(IO = IA\) (tính chất đường trung trực của đoạn thẳng)

Vì \(KI\) là đường trung trực của \(OB\) nên \(IO = IB\) (tính chất đường trung trực của đoạn thẳng)

Do đó \(IA = IB\,\,(= IO)\)

Xét \(\Delta OIA\) và \(\Delta OIB\) có:

\(IA = IB\) (cmt)

\(IO\) là cạnh chung

\(OA = OB\) (gt)

Do đó \(\Delta OIA = \Delta OIB\, (c.c.c) \Rightarrow \widehat {{O_1}} = \widehat {{O_2}}\) (hai góc tương ứng)

Vậy \(OI\) là tia phân giác của \(\widehat {xOy}\). Đáp án A đúng

Theo giả thiết: \(OA = OB\) suy ra \(O\) thuộc đường trung trực của đoạn thẳng \(AB\).

Theo chứng minh trên ta có \(IA = IB\) suy ra \(I\) thuộc đường trung trực của đoạn thẳng \(AB\).

Do đó \(OI\) là đường trung trực của đoạn thẳng \(AB\).

Đáp án B đúng.