Cho hai góc kề bù trong đó có một góc bằng \({70^0}\) góc còn lại bằng bao nhiêu?
Hai góc kề bù có tổng số đo bằng \({180^0}\), trong đó có một góc bằng \({70^0}\)
Số đo góc còn lại là: \({180^0} - {70^0} = {110^0}\).
Gọi tia \(Ox\) là tia đối của tia \(Om\). Số đo \(\widehat {xOn}\) là:
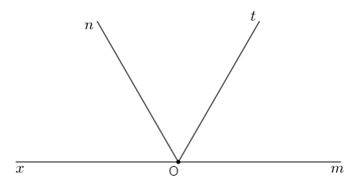
Vì \(Ox\) là tia đối của tia \(Om\) nên \(\widehat {xOn}\) và \(\widehat {mOn}\) là hai góc kề bù, do đó ta có:
\(\widehat {xOn} + \widehat {mOn} = {180^o}\)
\(\Rightarrow \widehat {xOn} = {180^o} - \widehat {mOn} \)\(\,= {180^o} - {120^o} = {60^o}\)
Số đo \(\widehat {nOt}\) là:
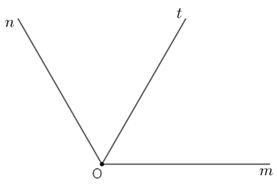
Trên cùng một nửa mặt phẳng bờ chứa tia \(Om\) có \(\widehat {mOn} > \,\widehat {mOt}\left( {{{120}^o} > {{60}^o}} \right)\) nên tia \(Ot\) nằm giữa hai tia \(Om,\,On.\)
Ta có: \(\widehat {mOt} + \widehat {nOt} = \widehat {mOn}\)
\(\begin{array}{l} \Rightarrow \widehat {nOt} = \widehat {mOn} - \widehat {mOt}\\ \Rightarrow \widehat {nOt} = {120^o} - {60^o} = {60^o}\end{array}\)
Số đo \(\widehat {nOt}\) là:

Trên cùng một nửa mặt phẳng bờ chứa tia \(Om\) có \(\widehat {mOn} > \,\widehat {mOt}\left( {{{120}^o} > {{60}^o}} \right)\) nên tia \(Ot\) nằm giữa hai tia \(Om,\,On.\)
Ta có: \(\widehat {mOt} + \widehat {nOt} = \widehat {mOn}\)
\(\begin{array}{l} \Rightarrow \widehat {nOt} = \widehat {mOn} - \widehat {mOt}\\ \Rightarrow \widehat {nOt} = {120^o} - {60^o} = {60^o}\end{array}\)
Số nghịch đảo của \(\dfrac{{ - 6}}{{11}}\) là:
Ta có số nghịch đảo của \(\dfrac{A}{B}\) là \(\dfrac{B}{A}\).
Do đó số nghịch đảo của \(\dfrac{{ - 6}}{{11}}\) là \( \dfrac{{11}}{{ - 6}}\).
Cho \(\widehat {xOy}\) có số đo \({78^o}\) và \(Ot\) là tia phân giác của \(\widehat {xOy}.\) Số đo của \(\widehat {xOt}\) là:
Vì \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \dfrac{1}{2}\widehat {xOy} = \dfrac{1}{2}{.78^o} = {39^o}\)
Chọn câu phát biểu đúng. Cho đường tròn \(\left( {O;R} \right)\).
Đường tròn \(\left( {O;R} \right)\) thì điểm \(O\) cách đều mọi điểm trên đường tròn một khoảng \(R.\)
Cho biết \(\dfrac{{x + 1}}{3} = \dfrac{{ - 8}}{{12}}\) . Khi đó giá trị của \(x\) là:
\(\begin{array}{l}
\dfrac{{x + 1}}{3} = \dfrac{{ - 8}}{{12}}\\
\Rightarrow \dfrac{{x + 1}}{3} = \dfrac{{ - 2}}{3}\\
\Rightarrow x + 1 = - 2\\
\Rightarrow x = - 2 - 1 = - 3
\end{array}\)
Ước của \( - 7\) là:
Các ước của \( - 7\) là \( - 7; - 1;1;7\).
Kết quả của phép tính \(\dfrac{3}{7}:\dfrac{5}{{28}}\) là:
\(\dfrac{3}{7}:\dfrac{5}{{28}} = \dfrac{3}{7}.\dfrac{{28}}{5} = \dfrac{{12}}{5}\)
Kết quả của phép tính: \(\left[ {94 - \left( {21 - 7} \right)} \right]:16\) là:
\(\begin{array}{l}\left[ {94 - \left( {21 - 7} \right)} \right]:16\\ = \left[ {94 - 14} \right]:16\\ = 80:16 = 5\end{array}\)
Biết \(\widehat A + \widehat B + \widehat C = {180^o};\widehat A = 2\widehat B;\widehat C = 3\widehat B.\) Số đo \(\widehat B\) là :
Thay \(\widehat A = 2\widehat B;\,\widehat C = 3\widehat B\) vào công thức \(\widehat A + \widehat B + \widehat C = {180^o}\) ta được :
\(\begin{array}{l}2\widehat B + \widehat B + 3\widehat B = {180^o}\\ \Rightarrow \widehat B.\left( {2 + 1 + 3} \right) = {180^o}\\ \Rightarrow6\widehat B = {180^o}\\ \Rightarrow \widehat B = {180^o}:6 = {30^o}\end{array}\)
Cho các số sau: \(\dfrac{{ - 3}}{2};\,\dfrac{3}{2};\,0;\,\dfrac{{ - 2}}{{ - 7}};\,\dfrac{5}{{ - 2}}\). Thứ tự sắp xếp các số từ nhỏ đến lớn là:
Ta có : \(\dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\)
Suy ra \( \dfrac{5}{{ - 2}} < \dfrac{{ - 3}}{2} < 0\)
\(\dfrac{{ - 2}}{{ - 7}} = \dfrac{2}{7} = \dfrac{4}{{14}};\,\dfrac{3}{2} = \dfrac{{21}}{{14}}\)
Do đó \(0 < \dfrac{4}{{14}} < \dfrac{{21}}{{14}}\)
Hay \( 0 < \dfrac{{ - 2}}{{ - 7}} < \dfrac{3}{2}\)
Thứ tự sắp xếp các số từ nhỏ đến lớn là: \(\dfrac{5}{{ - 2}} < \dfrac{{ - 3}}{2} < 0 < \dfrac{{ - 2}}{{ - 7}} < \dfrac{3}{2}\)
Biết \(\,3.\left| x \right| - \dfrac{1}{3} = \dfrac{8}{3}\). Các giá trị của \(x\) là:
\(\begin{array}{l}\,3.\left| x \right| - \dfrac{1}{3} = \dfrac{8}{3}\\\,\,\,\,3.\left| x \right|\,\,\,\,\,\,\, = \dfrac{8}{3} + \dfrac{1}{3}\\ \,\,\,\, 3.\left| x \right|\,\,\,\,\,\,\, = \dfrac{9}{3}\\\,\,\,\,3.\left| x \right|\,\,\,\,\,\,\, = 3\\\,\,\,\,\,\,\,\,\left| x \right|\,\,\,\,\,\,\, \;=3:3 \\\,\,\,\,\,\,\,\,\left| x \right|\,\,\,\,\,\,\, \;= 1\end{array}\)
Suy ra \(x = 1\) hoặc \(x = - 1\)
Một cửa hàng bán một tấm vải trong \(4\) ngày. Ngày thứ nhất bán \(\dfrac{1}{6}\) tấm vải và \(5m;\) ngày thứ hai bán \(20\% \) số vải còn lại và \(10m;\) ngày thứ ba tiếp tục bán \(25\%\) số vải còn lại và \(9m\) ; ngày thứ tư bán \(\dfrac{1}{3}\) số vải còn lại, cuối cùng còn \(13m.\) Tấm vải lúc đầu dài:
Số mét vải của ngày thứ tư khi chưa bán là: \(13:\left( {1 - \dfrac{1}{3}} \right) = \dfrac{{39}}{2}\left( m \right)\)
Số mét vải của ngày thứ ba khi chưa bán là: \(\left( {\dfrac{{39}}{2} + 9} \right):\left( {1 - 25\% } \right) = 38\left( m \right)\)
Số mét vải của ngày thứ hai khi chưa bán là: \(\left( {38 + 10} \right):\left( {1 - 20\% } \right) = 60\left( m \right)\)
Số mét vải của ngày đầu tiên khi chưa bán là: \(\left( {60 + 5} \right):\left( {1 - \dfrac{1}{6}} \right) = 78\left( m \right)\)
Vậy lúc đầu tấm vải dài số mét là: \(78m\).
Biết \(\dfrac{4}{{15}}x - \dfrac{3}{{10}}x = - 1\dfrac{1}{5}\). Giá trị của \(x\) là:
\(\dfrac{4}{{15}}x - \dfrac{3}{{10}}x = - 1\dfrac{1}{5}\)
\(x.\left( {\dfrac{4}{{15}} - \dfrac{3}{{10}}} \right) = - \dfrac{6}{5}\)
\(x.\left( {\dfrac{8}{{30}} - \dfrac{9}{{30}}} \right) = - \dfrac{6}{5}\)
\(x.\left( {\dfrac{{ - 1}}{{30}}} \right) = - \dfrac{6}{5}\)
\(x = - \dfrac{6}{5}:\left( {\dfrac{{ - 1}}{{30}}} \right)\)
\(x = - \dfrac{6}{5}.\left( { - 30} \right) = 36\)
Cho biểu thức: \(A = - \dfrac{7}{{17}} + \dfrac{{ - 5}}{{19}} + \dfrac{{24}}{{17}} - \dfrac{{14}}{{19}}\) . Giá trị của A là:
\(\begin{array}{l}A = - \dfrac{7}{{17}} + \dfrac{{ - 5}}{{19}} + \dfrac{{24}}{{17}} - \dfrac{{14}}{{19}}\\A = \left( { - \dfrac{7}{{17}} + \dfrac{{24}}{{17}}} \right) + \left( {\dfrac{{ - 5}}{{19}} - \dfrac{{14}}{{19}}} \right)\\A = \dfrac{{17}}{{17}} + \dfrac{{ - 19}}{{19}} \\A= 1 + \left( { - 1} \right) = 0\end{array}\)
Biết \(\left| {5x - \dfrac{5}{7}} \right| + \dfrac{1}{2} = 50\% \). Giá trị của \(x\) là:
\(\begin{array}{l}\left| {5x - \dfrac{5}{7}} \right| + \dfrac{1}{2} = 50\% \\\left| {5x - \dfrac{5}{7}} \right| + \dfrac{1}{2} = \dfrac{{50}}{{100}}\\\left| {5x - \dfrac{5}{7}} \right| + \dfrac{1}{2} = \dfrac{1}{2}\\\left| {5x - \dfrac{5}{7}} \right| = \dfrac{1}{2} - \dfrac{1}{2}\\\left| {5x - \dfrac{5}{7}} \right| = 0\end{array}\)
Suy ra \(5x - \dfrac{5}{7} = 0\)
\(5x = \dfrac{5}{7}\)
\(x = \dfrac{5}{7}:5\)
\(x = \dfrac{5}{7}.\dfrac{1}{5} = \dfrac{1}{7}\)
Biết \(\dfrac{{ - 8}}{{13}} + \dfrac{7}{{17}} + \dfrac{{21}}{{13}} < x < \dfrac{{ - 9}}{{14}} + 4 + \dfrac{5}{{ - 14}}\,\,\left( {x \in \mathbb{Z}} \right)\). Giá trị của \(x\) là:
\(\dfrac{{ - 8}}{{13}} + \dfrac{7}{{17}} + \dfrac{{21}}{{13}} \)
\(= \left( {\dfrac{{ - 8}}{{13}} + \dfrac{{21}}{{13}}} \right) + \dfrac{7}{{17}} \)
\(= \dfrac{{13}}{{13}} + \dfrac{7}{{17}} = 1 + \dfrac{7}{{17}}\)
\(\dfrac{{ - 9}}{{14}} + 4 + \dfrac{5}{{ - 14}}\)
\(= \left( {\dfrac{{ - 9}}{{14}} + \dfrac{{ - 5}}{{14}}} \right) + 4\)
\(= \dfrac{{ - 14}}{{14}} + 4 = \left( { - 1} \right) + 4 = 3\)
Do đó \(1 + \dfrac{7}{{17}} < x < 3\)
Vậy \(x = 2\).
Trên cùng một nửa mặt phẳng bờ chứa tia \(Om\), vẽ hai tia \(On\) và \(Ot\) sao cho \(\widehat {mOn} = {120^o},\,\widehat {mOt} = {60^o}.\)
Số đo \(\widehat {nOt}\) là:

Trên cùng một nửa mặt phẳng bờ chứa tia \(Om\) có \(\widehat {mOn} > \,\widehat {mOt}\left( {{{120}^o} > {{60}^o}} \right)\) nên tia \(Ot\) nằm giữa hai tia \(Om,\,On.\)
Ta có: \(\widehat {mOt} + \widehat {nOt} = \widehat {mOn}\)
\(\begin{array}{l} \Rightarrow \widehat {nOt} = \widehat {mOn} - \widehat {mOt}\\ \Rightarrow \widehat {nOt} = {120^o} - {60^o} = {60^o}\end{array}\)

