Tập hợp các số nguyên là ước của \(2\) là:
Tập hợp các số nguyên là ước của \(2\) là \(\left\{ { - 2; - 1;1;2} \right\}\).
Số trang bạn Mai đọc trong ngày thứ ba chiếm số phần trăm tổng số trang của cuốn sách là:
Sử dụng kết quả câu trên ngày thứ ba bạn Mai đọc được \(96\) trang.
Số trang bạn Mai đọc trong ngày thứ ba chiếm số phần trăm tổng số trang của cuốn sách là:
\(\dfrac{{96}}{{240}}.100\% = 40\% \)
Ngày thứ \(3\) Mai đọc được số trang sách là:
Ngày thứ nhất bạn Mai đọc được số trang sách là:
\(\dfrac{1}{3}.240 = 80\) (trang)
Số trang sách còn lại sau khi đọc xong ngày thứ nhất là:
\(240 - 80 = 160\) (trang)
Ngày thứ hai bạn Mai đọc được số trang sách là:
\(160.40\% = 160.\dfrac{{40}}{{100}} = 64\) (trang)
Ngày thứ ba bạn Mai đọc được số trang sách là:
\(240 - 80 - 64 = 96\) (trang)
Ngày thứ \(3\) Mai đọc được số trang sách là:
Ngày thứ nhất bạn Mai đọc được số trang sách là:
\(\dfrac{1}{3}.240 = 80\) (trang)
Số trang sách còn lại sau khi đọc xong ngày thứ nhất là:
\(240 - 80 = 160\) (trang)
Ngày thứ hai bạn Mai đọc được số trang sách là:
\(160.40\% = 160.\dfrac{{40}}{{100}} = 64\) (trang)
Ngày thứ ba bạn Mai đọc được số trang sách là:
\(240 - 80 - 64 = 96\) (trang)
Vẽ tia \(Ot\) là tia đối của tia \(Ox\), đường tròn tâm \(O\) bán kính \(3cm\) cắt đường thẳng \(xt\) tại hai điểm \(M,N\). Trên tia \(Ox\) lấy điểm \(P\) sao cho \(OP = 4cm\) . Độ dài đoạn thẳng \(NP\) là:
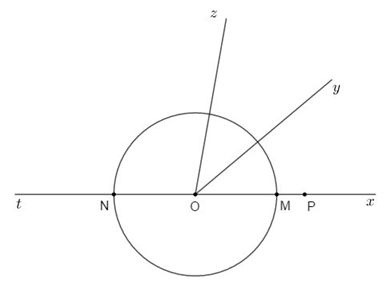
TH1:
\(\left( {O;3cm} \right)\) cắt \(Ox\) tại \(M\)và cắt \(Ot\) tại \(N\).
Ta có \(P\) nằm trên \(Ox\), \(N\) nằm trên \(Ot\) mà \(Ox\) và \(Ot\) là hai tia đối nhau nên \(O\) nằm giữa hai điểm \(N\) và \(P.\)
Ta có: \(NP = NO + OP = 3 + 4 = 7\left( {cm} \right).\)
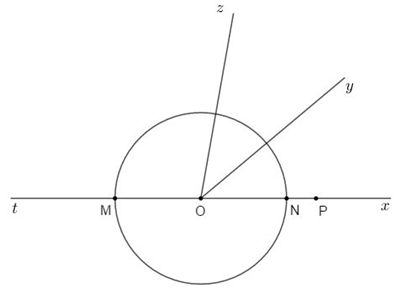
TH2:
\(\left( {O;3cm} \right)\) cắt \(Ox\) tại \(N\) và cắt \(Ot\) tại \(M.\)
Trên tia \(Ox\) ta có \(ON < OP\,\left( {3cm < 4cm} \right)\) nên \(N\) nằm giữa \(O\) và \(P.\)
Ta có: \(ON + NP = OP\)
\( \Rightarrow NP = OP - ON = 4 - 3 = 1\left( {cm} \right).\)
Vẽ tia \(Ot\) là tia đối của tia \(Ox\). Số đo góc \(\widehat {yOt}\) là:
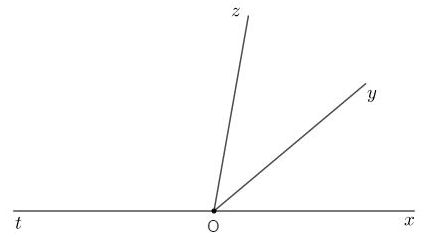
\(Ot\) là tia đối của tia \(Ox\) nên \(\widehat {xOy}\) và \(\widehat {yOt}\) là hai góc kề bù nên ta có:
\(\widehat {xOy} + \widehat {yOt} = {180^o}\)
\(\Rightarrow \widehat {yOt} = {180^o} - \widehat {xOy}\)\(\, = {180^o} - {40^o} = {140^o}\)
Số đo \(\widehat {yOz}\) bằng:
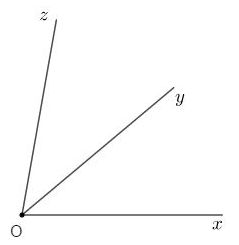
Vì trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\), \(\widehat {xOy} < \widehat {xOz}\,\left( {{{40}^o} < {{80}^o}} \right)\) nên tia \(Oy\) nằm giữa hai tia \(Ox,\,Oz\).
Ta có: \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
\( \Rightarrow \widehat {yOz} = \widehat {xOz} - \widehat {xOy} = {80^o} - {40^o} = {40^o}.\)
Số đo \(\widehat {yOz}\) bằng:

Vì trên cùng một nửa mặt phẳng có bờ chứa tia \(Ox\), \(\widehat {xOy} < \widehat {xOz}\,\left( {{{40}^o} < {{80}^o}} \right)\) nên tia \(Oy\) nằm giữa hai tia \(Ox,\,Oz\).
Ta có: \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)
\( \Rightarrow \widehat {yOz} = \widehat {xOz} - \widehat {xOy} = {80^o} - {40^o} = {40^o}.\)
Kết quả của phép tính \(7 + \left( { - 8} \right)\) là:
\(7 + \left( { - 8} \right) = - \left( {8 - 7} \right) = - 1.\)
Kết quả của phép tính \(\dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} + \dfrac{4}{{31}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} + \dfrac{3}{{31}}}}\) là:
\(\dfrac{{\dfrac{4}{{17}} - \dfrac{4}{{49}} + \dfrac{4}{{31}}}}{{\dfrac{3}{{17}} - \dfrac{3}{{49}} + \dfrac{3}{{31}}}} = \dfrac{{4.\left( {\dfrac{1}{{17}} - \dfrac{1}{{49}} + \dfrac{1}{{31}}} \right)}}{{3.\left( {\dfrac{1}{{17}} - \dfrac{1}{{49}} + \dfrac{1}{{31}}} \right)}} = \dfrac{4}{3}\)
Số không phải là số nghịch đảo của \(\dfrac{{ - 3}}{7}\) là:
Ta có:
\(\dfrac{{ - 3}}{7}.\dfrac{{ - 7}}{3} = \dfrac{{\left( { - 3} \right).\left( { - 7} \right)}}{{7.3}} = 1\) \( \Rightarrow \) \(\dfrac{{ - 7}}{3}\) là số nghịch đảo của \(\dfrac{{ - 3}}{7}\).
\(\dfrac{{ - 3}}{7}.\left( { - \dfrac{7}{3}} \right) = \dfrac{{ - 3}}{7}.\dfrac{{ - 7}}{3} = \dfrac{{\left( { - 3} \right).\left( { - 7} \right)}}{{7.3}} = 1\) \( \Rightarrow \) \( - \dfrac{7}{3}\) là số nghịch đảo của \(\dfrac{{ - 3}}{7}\).
\(\dfrac{{ - 3}}{7}.\dfrac{7}{{ - 3}} = \dfrac{{\left( { - 3} \right).7}}{{7.\left( { - 3} \right)}} = 1\) \( \Rightarrow \) \(\dfrac{7}{{ - 3}}\) là số nghịch đảo của \(\dfrac{{ - 3}}{7}\).
\(\dfrac{{ - 3}}{7}.\dfrac{7}{3} = \dfrac{{\left( { - 3} \right).7}}{{7.3}} = - 1\) \( \Rightarrow \) \(\dfrac{7}{3}\) không là số nghịch đảo của \(\dfrac{{ - 3}}{7}\).
\(\dfrac{2}{3}\) của \( - 12\) bằng:
\(\dfrac{2}{3}\) của \( - 12\) bằng: \(\dfrac{2}{3}.\left( { - 12} \right) = \dfrac{{2.\left( { - 12} \right)}}{3} = - 8.\)
Cho góc \(xOy\) và góc \(yOz\) là hai góc phụ nhau. Nếu góc \(xOy\) bằng \({50^o}\)thì số đo góc \(yOz\) là:
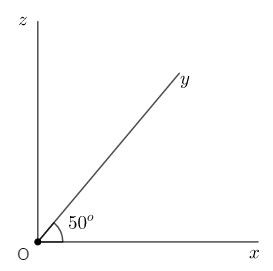
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc phụ nhau nên ta có:
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = {90^o}\\ \Rightarrow \widehat {yOz} = {90^o} - \widehat {xOy} = {90^o} - {50^o} = {40^o}.\end{array}\)
Cho đoạn thẳng \(AB = 5cm\). Đường tròn \(\left( {A;3cm} \right)\) cắt đoạn \(AB\) tại \(C\). Khi đó độ dài của đoạn thẳng \(BC\) là:
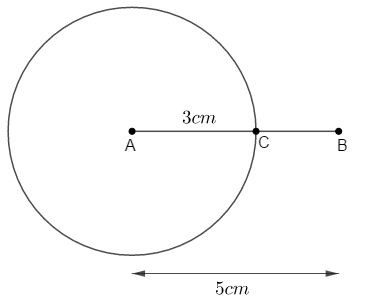
Đường tròn \(\left( {A;3cm} \right)\) cắt đoạn \(AB\) tại \(C\) nên \(C\) nằm giữa hai điểm \(A,\,B.\)
\(C\) là điểm nằm trên \(\left( {A;3cm} \right)\) nên \(AC = 3\,cm.\)
Ta có: \(AC + BC = AB\)
\( \Rightarrow BC = AB - AC = 5 - 3 = 2\,\left( {cm} \right).\)
Số nguyên \(x\) thỏa mãn điều kiện \(\dfrac{{ - 6}}{{15}} < \dfrac{x}{{15}} < \dfrac{{ - 4}}{{15}}\) là:
Có \(\dfrac{{ - 6}}{{15}};\dfrac{x}{{15}};\dfrac{{ - 4}}{{15}}\) là các phân số có cùng mẫu dương.
Do đó \(\dfrac{{ - 6}}{{15}} < \dfrac{x}{{15}} < \dfrac{{ - 4}}{{15}}\) suy ra \( - 6 < x < - 4\).
Mà \(x \in \mathbb{Z}\) nên \(x = - 5.\)
Khoanh vào chữ cái trước kết quả đúng.
Cho hai góc \(xOy\) và \(yOz\) kề bù và \(\widehat {xOy} = 2\widehat {yOz}\) . Số đo \(\widehat {xOy}\) là:
Vì \(\widehat {xOy}\) và \(\widehat {yOz}\) là hai góc kề bù nên ta có:
\(\begin{array}{l}\widehat {xOy} + \widehat {yOz} = {180^o}\\ \Rightarrow 2\widehat {yOz} + \widehat {yOz} = {180^o}\\ \Rightarrow 3\widehat {yOz} = {180^o}\\ \Rightarrow \widehat {yOz} = {180^o}:3 = {60^o}\\ \Rightarrow \widehat {xOy} = 2\widehat {yOz} = {2.60^o} = {120^o}.\end{array}\)
Biểu thức \(\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\) có giá trị bằng:
\(\begin{array}{l}\dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} - \dfrac{5}{7}.\dfrac{8}{{13}}\\ = \dfrac{{ - 5}}{7}.\dfrac{2}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{3}{{13}} + \dfrac{{ - 5}}{7}.\dfrac{8}{{13}}\\ = \dfrac{{ - 5}}{7}.\left( {\dfrac{2}{3} + \dfrac{3}{{13}} + \dfrac{8}{{13}}} \right)\\ = \dfrac{{ - 5}}{7}.\dfrac{{13}}{{13}} = \dfrac{{ - 5}}{7}.1 = \dfrac{{ - 5}}{7}\end{array}\)
Biết \(\dfrac{{ - 4}}{5}x + 1\dfrac{1}{3}x = - 1\dfrac{1}{3}\), giá trị của \(x\) là:
\(\begin{array}{l}\dfrac{{ - 4}}{5}x + 1\dfrac{1}{3}x = - 1\dfrac{1}{3}\\\dfrac{{ - 4}}{5}x + \dfrac{4}{3}x = \dfrac{{ - 4}}{3}\\x.\left( {\dfrac{{ - 4}}{5} + \dfrac{4}{3}} \right) = \dfrac{{ - 4}}{3}\\x.\left( {\dfrac{{ - 12}}{{15}} + \dfrac{{20}}{{15}}} \right) = \dfrac{{ - 4}}{3}\\\dfrac{8}{{15}}x = \dfrac{{ - 4}}{3}\\x = \dfrac{{ - 4}}{3}:\dfrac{8}{{15}}\\x = \dfrac{{ - 4}}{3}.\dfrac{{15}}{8}\\x = \dfrac{{ - 5}}{2}\end{array}\)
Kết quả của phép tính \(75\% - 1\dfrac{1}{5} + 0,5:\dfrac{5}{{12}} - \left( {\dfrac{{ - 1}}{4}} \right)\) là:
\(\begin{array}{l}75\% - 1\dfrac{1}{5} + 0,5:\dfrac{5}{{12}} - \left( {\dfrac{{ - 1}}{4}} \right)\\ = \dfrac{{75}}{{100}} - \dfrac{6}{5} + \dfrac{1}{2}:\dfrac{5}{{12}} + \dfrac{1}{4}\\ = \dfrac{3}{4} - \dfrac{6}{5} + \dfrac{1}{2}.\dfrac{{12}}{5} + \dfrac{1}{4}\\ = \dfrac{3}{4} - \dfrac{6}{5} + \dfrac{6}{5} + \dfrac{1}{4}\\ = \left( {\dfrac{3}{4} + \dfrac{1}{4}} \right) + \left( {\dfrac{6}{5} - \dfrac{6}{5}} \right)\\ = \dfrac{4}{4} + 0 = 1\end{array}\)
Bạn Mai đọc một cuốn sách dày \(240\) trang trong \(3\) ngày. Ngày thứ nhất bạn đọc \(\dfrac{1}{3}\) tổng số trang sách. Ngày thứ hai bạn đọc được \(40\% \) số trang sách còn lại.
Ngày thứ \(3\) Mai đọc được số trang sách là:
Ngày thứ nhất bạn Mai đọc được số trang sách là:
\(\dfrac{1}{3}.240 = 80\) (trang)
Số trang sách còn lại sau khi đọc xong ngày thứ nhất là:
\(240 - 80 = 160\) (trang)
Ngày thứ hai bạn Mai đọc được số trang sách là:
\(160.40\% = 160.\dfrac{{40}}{{100}} = 64\) (trang)
Ngày thứ ba bạn Mai đọc được số trang sách là:
\(240 - 80 - 64 = 96\) (trang)

