Hai đường thẳng xx’ và yy’ cắt nhau tại \(O\). Góc đối đỉnh với \(\widehat {xOy'}\) là:
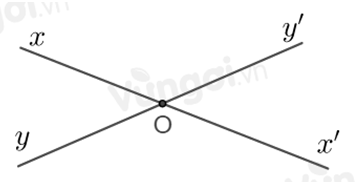
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên \(Ox'\) là tia đối của tia \(Ox\), \(Oy\) là tia đối của tia \(Oy'.\) Vậy góc đối đỉnh với \(\widehat {xOy'}\) là \(\widehat {x'Oy}\).
Cho góc \(xOy\) đối đỉnh với góc \(x'Oy'\) và \(\widehat {xOy} = 120^\circ \). Tính số đo góc \(x'Oy'\).
Vì góc \(xOy\) đối đỉnh với góc \(x'Oy'\) nên \(\widehat {x'Oy'} = \widehat {xOy}\) (tính chất hai góc đối đỉnh)
Mà \(\widehat {xOy} = {120^0}\)
Do đó \(\widehat {x'Oy'} = {120^0}\).
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {x'Oy} = 55^\circ \). Chọn câu sai.
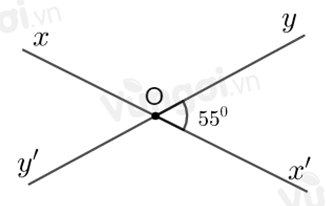
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên hai tia \(Ox\) và \(Ox'\) là hai tia đối nhau; hai tia \(Oy\) và \(Oy'\) là hai tia đối nhau.
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\); \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {xOy'} = \widehat {x'Oy} = {55^0}\) và \(\widehat {x'Oy'} = \widehat {xOy}\)
Lại có: \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
\( \Rightarrow \widehat {xOy} + {55^0} = {180^0}\)
\( \Rightarrow \widehat {xOy} = {180^0} - {55^0} = {125^0}\)
Vậy \(\widehat {xOy'} = \widehat {x'Oy} = {55^0}\) và \(\widehat {x'Oy'} = \widehat {xOy} = {125^0}\)
Suy ra A, C, D đúng, B sai.
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và \(Oz'\) là hai tia đối nhau). Biết \(3.\widehat {tOz'} = \widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
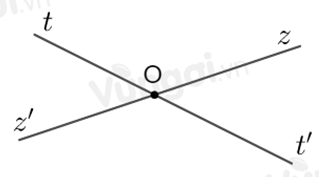
Vì \(\widehat {tOz'}\) và \(\widehat {tOz}\) là hai góc kề bù nên \(\widehat {tOz} + \widehat {tOz'} = {180^0}\)
Mà \(3.\widehat {tOz'} = \widehat {tOz}\)
\( \Rightarrow 3.\widehat {tOz'} + \widehat {tOz'} = {180^0}\) \( \Rightarrow 4.\widehat {tOz'} = {180^0}\) \( \Rightarrow \widehat {tOz'} = {45^0}\)
Khi đó \(\widehat {tOz} = 3.\widehat {tOz'} = {3.45^0} = {135^0}\)
Vì \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) là hai góc đối đỉnh nên \(\widehat {t'Oz'} = \widehat {tOz} = {135^0}.\)
Vẽ \(\widehat {ABC} = {62^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\). Sau đó vẽ tiếp \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
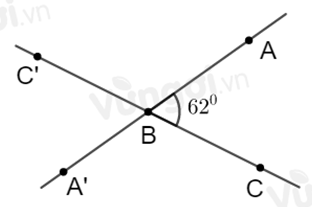
Vì \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\) nên tia \(BC'\) là tia đối của tia \(BC.\)
Vì \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\) nên tia \(BA'\) là tia đối của tia \(BA.\)
Do đó \(\widehat {C'BA'}\) và \(\widehat {CBA}\) là hai góc đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {CBA} = {62^0}\) (tính chất hai góc đối đỉnh).
Cho hình vẽ sau. Biết góc \(xOy'\) đối đỉnh với góc \(x'Oy,\) biết \(\widehat {xOy} = {\widehat O_4} = {20^o}\). Tính các góc đỉnh O (khác góc bẹt).
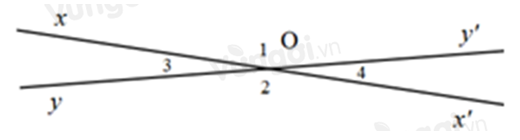
Vì \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\) là hai góc kề bù nên \(\widehat {{O_2}} + \widehat {{O_4}} = {180^0}\)
\( \Rightarrow \widehat {{O_2}} = {180^0} - \widehat {{O_4}}\)
\( \Rightarrow \widehat {{O_2}} = {180^0} - {20^0} = {160^0}\)
Vì \(\widehat {{O_1}}\) đối đỉnh với \(\widehat {{O_2}}\) nên \(\widehat {{O_1}} = \widehat {{O_2}} = {160^0}\) (tính chất hai góc đối đỉnh)
Vẽ góc \(xOy\) có số đo bằng 50o. Vẽ góc \(nOm\) đối đỉnh với góc \(xOy\) (\(Oy\) và \(Om\) là hai tia đối nhau). Viết tên các góc có số đo bằng 130o.
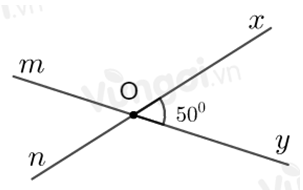
Vì \(\widehat {nOm}\) và \(\widehat {xOy}\) là hai góc đối đỉnh nên \(\widehat {nOm} = \widehat {xOy} = {50^0}\) (tính chất hai góc đối đỉnh)
Ta có: \(\widehat {xOy}\) và \(\widehat {xOm}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {xOm} = {180^0}\) \( \Rightarrow \widehat {xOm} = {180^0} - \widehat {xOy}\) \( \Rightarrow \widehat {xOm} = {180^0} - {50^0} = {130^0}\)
Do đó \(\widehat {xOm} = \widehat {yOn} = {130^0}\) (hai góc đối đỉnh)
Các góc có số đo bằng 130o: \(\widehat {xOm};\widehat {yOn}\).
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {124^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
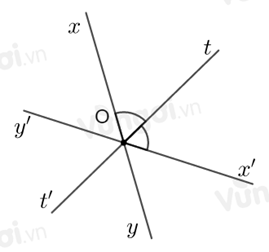
Vì \(Ot\) là tia phân giác của góc \(xOx'\) nên
\(\widehat {xOt} = \widehat {tOx'} = \dfrac{1}{2}\widehat {xOx'} = \dfrac{1}{2}{.124^o} = {62^o}\)
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O\) nên tia \(Oy\) là tia đối của tia \(Ox\)
Mà tia \(Ot'\) là tia đối của tia \(Ot\)
Suy ra \(\widehat {yOt'}\) và \(\widehat {xOt}\) là hai góc đối đỉnh.
\( \Rightarrow \widehat {yOt'} = \widehat {xOt} = {62^o}\) (tính chất hai góc đối đỉnh).
Trên đường thẳng \(AA'\) lấy điểm \(O.\) Vẽ trên cùng nửa mặt phẳng bờ \(AA'\) tia \(OB\) và tia \(OD\) sao cho \(\widehat {AOB} = \widehat {A'OD} = {45^o}.\) Tính góc \(BOD.\)
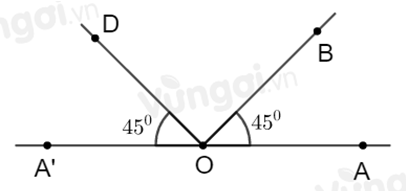
Vì \(\widehat {AOD}\) và \(\widehat {DOA'}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {DOA'} = {180^0}\)
\( \Rightarrow \widehat {AOD} = {180^0} - \widehat {DOA'}\)
\( \Rightarrow \widehat {AOD} = {180^0} - {45^0} = {135^0}\)
Ta có: tia \(OB\) và tia \(OD\) nằm trên cùng một nửa mặt phẳng có bờ chứa tia \(OA\) và \(\widehat {AOB} < \widehat {AOD}\,(do\,{45^o} < {135^o})\) nên tia \(OB\) nằm giữa hai tia \(OA\) và \(OD\).
Do đó \(\widehat {AOB} + \widehat {BOD} = \widehat {AOD}\) \( \Rightarrow {45^0} + \widehat {BOD} = {135^0}\) \( \Rightarrow \widehat {BOD} = {135^0} - {45^0} = {90^0}\).
Cho \(\widehat {AOB} = 60^\circ \), tia \(OC\) là tia phân giác của \(\widehat {AOB}\). Gọi \(OD\) là tia đối của tia \(OA\). Trên nửa mặt phẳng bờ \(AD\) không chứa tia \(OB\), vẽ tia \(OI\) sao cho \(\widehat {DOI} = 30^\circ \). Góc nào dưới đây đối đỉnh với \(\widehat {AOC}\).
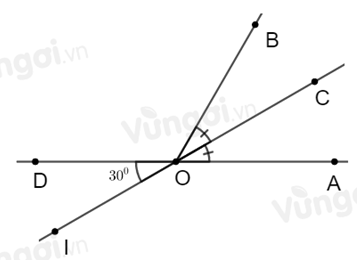
Vì tia \(OD\) là tia đối của tia \(OA\) nên \(\widehat {DOI}\) và \(\widehat {AOI}\) là hai góc kề bù.
Khi đó \(\widehat {DOI} + \widehat {AOI} = 180^\circ \) \( \Rightarrow \widehat {AOI} = {180^0} - \widehat {DOI}\) \( \Rightarrow \widehat {AOI} = {180^0} - {30^0} = {150^0}\)
Vì \(OC\) là tia phân giác của \(\widehat {AOB}\) nên \(\widehat {AOC} = \dfrac{{\widehat {AOB}}}{2} = \dfrac{{{{60}^0}}}{2} = {30^0}\)
Xét hai góc kề \(\widehat {AOI}\) và \(\widehat {AOC}\) ta có: \(\widehat {AOI} + \widehat {AOC} = {150^0} + {30^0} = {180^0}\) suy ra \(\widehat {AOI}\) và \(\widehat {AOC}\) là hai góc kề bù.
Do đó tia \(OI\) là tia đối của tia \(OC\).
Mặt khác tia \(OD\) là tia đối của tia \(OA\) nên \(\widehat {DOI}\) và \(\widehat {AOC}\) là hai góc đối đỉnh.
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) tạo thành \(\widehat {AOC} = 100^\circ \). Gọi \(OM\) là phân giác \(\widehat {AOC}\) và \(ON\) là tia đối của tia \(OM\). Tính \(\widehat {BON}\) và \(\widehat {DON}.\)
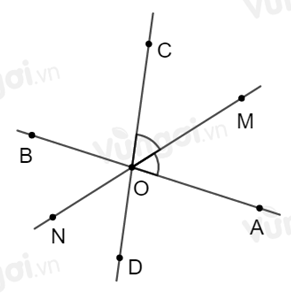
Vì \(OM\) là tia phân giác \(\widehat {AOC}\) nên \(\widehat {AOM} = \widehat {COM} = \dfrac{{\widehat {AOC}}}{2} = \dfrac{{{{100}^0}}}{2} = {50^0}\)
Vì \(AB\) và \(CD\) cắt nhau tại \(O\) nên \(OB\) là tia đối của tia \(OA\), \(OD\) là tia đối của tia \(OC\)
Mặt khác \(ON\) là tia đối của tia \(OM\) nên \(\widehat {AOM}\) và \(\widehat {BON}\) là hai góc đối đỉnh; \(\widehat {COM}\) và \(\widehat {DON}\) là hai góc đối đỉnh.
Suy ra \(\widehat {BON} = \widehat {AOM} = {50^0};\widehat {DON} = \widehat {COM} = {50^0}\) hay \(\widehat {BON} = \widehat {DON} = {50^0}.\)
Hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O.\) Biết \(\widehat {AOC} = 3\widehat {AOD}.\) Chọn câu sai.
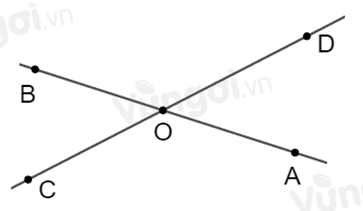
Vì \(\widehat {AOD}\) và \(\widehat {AOC}\) là hai góc kề bù nên \(\widehat {AOD} + \widehat {AOC} = 180^\circ \) mà \(\widehat {AOC} = 3\widehat {AOD}\)
\( \Rightarrow \widehat {AOD} + 3\widehat {AOD} = 180^\circ \) \( \Rightarrow 4\widehat {AOD} = 180^\circ \) \( \Rightarrow \widehat {AOD} = 180^\circ :4 = 45^\circ \)
Do đó \(\widehat {AOC} = 3\widehat {AOD} = {3.45^0} = {135^0}\)
Vì hai đường thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) nên hai tia \(OB\) và \(OA\) là hai tia đối nhau, hai tia \(OD\) và \(OC\) là hai tia đối nhau.
Do đó \(\widehat {BOD}\) và \(\widehat {AOC}\) là hai góc đối đỉnh; \(\widehat {AOD}\) và \(\widehat {BOC}\) là hai góc đối đỉnh
Kh đó \(\widehat {BOD} = \widehat {AOC} = 135^\circ ;\)\(\widehat {BOC} = \widehat {AOD} = 45^\circ \)
Vậy \(\widehat {BOD} = \widehat {AOC} = 135^\circ ;\) \(\widehat {BOC} = \widehat {AOD} = 45^\circ \).
Vẽ tia $Ot$ là tia phân giác của góc $MOP,$ $Ot'$ là tia đối của tia $Ot.$ Chọn câu đúng.
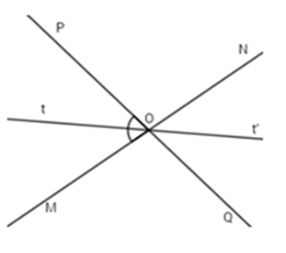
Vì $Ot$ là tia phân giác của góc $MOP$ nên $\widehat {MOt} = \widehat {tOP} = \dfrac{1}{2}\widehat {MOP} = \dfrac{1}{2}{.80^o} = {40^o}.$
Vì $Ot'$ là tia đối của tia $Ot,$ do đó :
\(\widehat {NOt'} = \widehat {MOt} = {40^o}\,\,\,\) (hai góc đối đỉnh)
\(\widehat {t'OQ} = \widehat {tOP} = {40^o}\,\,\,\,\) (hai góc đối đỉnh)
\( \Rightarrow \widehat {NOt'} = \widehat {t'OQ}\)
Mặt khác tia $Ot'$ nằm trong góc $NOQ.$ Vậy $Ot'$ là tia phân giác của góc $NOQ.$
Chọn câu đúng.
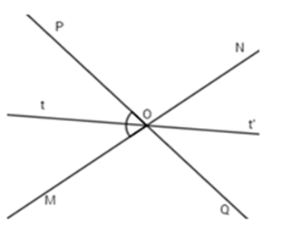
$\widehat {NOQ} = \widehat {MOP} = {80^o}$ (tính chất hai góc đối đỉnh)
Vì góc $MOP$ và $PON$ là hai góc kề bù nên :
$\,\widehat {MOP} + \widehat {PON} = {180^o} \Rightarrow {80^o} + \widehat {PON} = {180^o}$ $ \Rightarrow \widehat {PON} = {180^o} - {80^o} = {100^o}$
Khi đó $\widehat {MOQ} = \widehat {PON} = {100^o}$ (tính chất hai góc đối đỉnh).
Chọn câu đúng.

$\widehat {NOQ} = \widehat {MOP} = {80^o}$ (tính chất hai góc đối đỉnh)
Vì góc $MOP$ và $PON$ là hai góc kề bù nên :
$\,\widehat {MOP} + \widehat {PON} = {180^o} \Rightarrow {80^o} + \widehat {PON} = {180^o}$ $ \Rightarrow \widehat {PON} = {180^o} - {80^o} = {100^o}$
Khi đó $\widehat {MOQ} = \widehat {PON} = {100^o}$ (tính chất hai góc đối đỉnh).
Chọn câu đúng.

$\widehat {NOQ} = \widehat {MOP} = {80^o}$ (tính chất hai góc đối đỉnh)
Vì góc $MOP$ và $PON$ là hai góc kề bù nên :
$\,\widehat {MOP} + \widehat {PON} = {180^o} \Rightarrow {80^o} + \widehat {PON} = {180^o}$ $ \Rightarrow \widehat {PON} = {180^o} - {80^o} = {100^o}$
Khi đó $\widehat {MOQ} = \widehat {PON} = {100^o}$ (tính chất hai góc đối đỉnh).
Hai đường thẳng zz’ và tt’ cắt nhau tại $A$. Góc đối đỉnh với \(\widehat {zAt'}\) là:
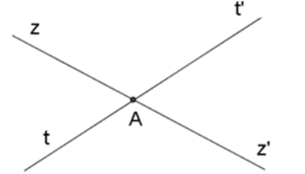
Vì hai đường thẳng $zz'$ và $tt'$ cắt nhau tại $A$ nên $Az'$ là tia đối của tia $Az,At'$ là tia đối của tia $At.$ Vậy góc đối đỉnh với \(\widehat {zAt'}\) là \(\widehat {z'At}\).
Cho góc \(xBy\) đối đỉnh với góc \(x'By'\) và \(\widehat {xBy} = 60^\circ \) . Tính số đo góc \(x'By'.\)
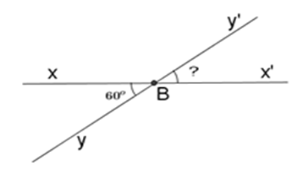
Vẽ \(\widehat {x'By'}\) là góc đối đỉnh với \(\widehat {xBy}\). Khi đó:
\(\widehat {x'By'} = \widehat {xBy} = {60^o}\) (tính chất hai góc đối đỉnh)
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {xOy} = 45^\circ \) . Chọn câu sai.
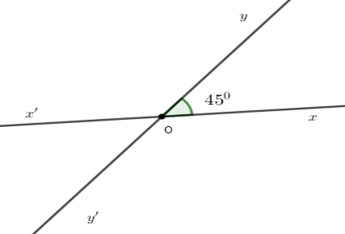
Vì hai đường thẳng $xx'$ và $yy'$ cắt nhau tại $O$ nên $Ox'$ là tia đối của tia $Ox;Oy'$ là tia đối của tia $Oy.$
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\) ; \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'}\)
Lại có \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc ở vị trí kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)\( \Rightarrow 45^\circ + \widehat {x'Oy} = 180^\circ \Rightarrow \widehat {x'Oy} = 180^\circ - 45^\circ \)
\( \Rightarrow \widehat {x'Oy} = 135^\circ \)
Vậy \(\widehat {x'Oy'} = \widehat {xOy} = 45^\circ \) và \(\widehat {x'Oy} = \widehat {xOy'} = 135^\circ .\)
Suy ra A, B, C đúng, D sai.
Cho cặp góc đối đỉnh \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) (\(Oz\) và $Oz'$ là hai tia đối nhau). Biết \(\widehat {tOz'} = 4.\widehat {tOz}\). Tính các góc \(\widehat {tOz}\) và \(\widehat {t'Oz'}.\)
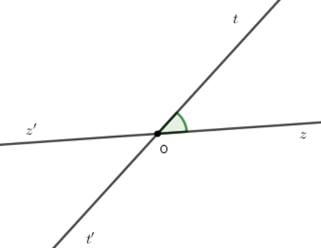
Ta có \(\widehat {zOt} + \widehat {tOz'} = 180^\circ \) (hai góc kề bù) mà \(\widehat {tOz'} = 4.\widehat {tOz}\) \( \Rightarrow \widehat {zOt} + 4.\widehat {zOt} = 180^\circ \) \( \Rightarrow 5.\widehat {zOt} = 180^\circ \Rightarrow \widehat {zOt} = 36^\circ \)
Vì \(\widehat {tOz}\) và \(\widehat {t'Oz'}\) là hai góc đối đỉnh nên \(\widehat {zOt} = \widehat {z'Ot'} = 36^\circ .\)

