Câu hỏi:
2 năm trước
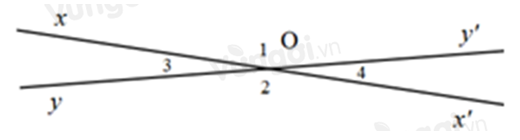
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O.\) Biết \(\widehat {xOx'} = {124^o}\). \(Ot\) là tia phân giác của góc xOx’. \(Ot'\) là tia đối của tia \(Ot.\) Tính số đo góc \(yOt'.\)
Trả lời bởi giáo viên
Đáp án đúng: a
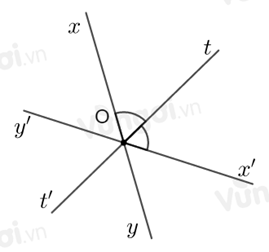
Vì \(Ot\) là tia phân giác của góc \(xOx'\) nên
\(\widehat {xOt} = \widehat {tOx'} = \dfrac{1}{2}\widehat {xOx'} = \dfrac{1}{2}{.124^o} = {62^o}\)
Hai đường thẳng \(xy\) và \(x'y'\) cắt nhau tại \(O\) nên tia \(Oy\) là tia đối của tia \(Ox\)
Mà tia \(Ot'\) là tia đối của tia \(Ot\)
Suy ra \(\widehat {yOt'}\) và \(\widehat {xOt}\) là hai góc đối đỉnh.
\( \Rightarrow \widehat {yOt'} = \widehat {xOt} = {62^o}\) (tính chất hai góc đối đỉnh).
Hướng dẫn giải:
+ Sử dụng tính chất tia phân giác của một góc để tính \(\widehat {xOt};\widehat {tOx'}\): “Nếu tia \(Oz\) là tia phân giác của góc \(xOy\) thì \(\widehat {xOz} = \widehat {yOz} = \dfrac{{\widehat {xOy}}}{2}\).
+ Sử dụng định nghĩa hai góc đối đỉnh: “Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia” để xác định góc đối đỉnh với \(\widehat {yOt'}\), sau đó áp dụng tính chất hai góc đối đỉnh: “Hai góc đối đỉnh thì bằng nhau” để tính \(\widehat {yOt'}\).
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
