Câu hỏi:
3 năm trước
Cho hình vẽ sau. Biết góc \(xOy'\) đối đỉnh với góc \(x'Oy,\) biết \(\widehat {xOy} = {\widehat O_4} = {20^o}\). Tính các góc đỉnh O (khác góc bẹt).
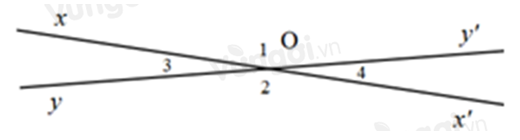
Trả lời bởi giáo viên
Đáp án đúng: b
Vì \(\widehat {{O_2}}\) và \(\widehat {{O_4}}\) là hai góc kề bù nên \(\widehat {{O_2}} + \widehat {{O_4}} = {180^0}\)
\( \Rightarrow \widehat {{O_2}} = {180^0} - \widehat {{O_4}}\)
\( \Rightarrow \widehat {{O_2}} = {180^0} - {20^0} = {160^0}\)
Vì \(\widehat {{O_1}}\) đối đỉnh với \(\widehat {{O_2}}\) nên \(\widehat {{O_1}} = \widehat {{O_2}} = {160^0}\) (tính chất hai góc đối đỉnh)
Hướng dẫn giải:
+ Sử dụng: Hai góc kề bù có tổng bằng \({180^0}.\)
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau.

