Vẽ \(\widehat {ABC} = {62^o}\). Vẽ \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\). Sau đó vẽ tiếp \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\). Tính số đo \(\widehat {C'BA'}\).
Trả lời bởi giáo viên
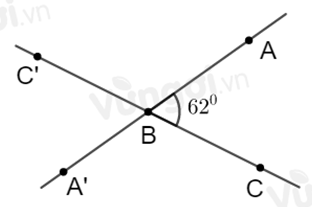
Vì \(\widehat {ABC'}\) kề bù với \(\widehat {ABC}\) nên tia \(BC'\) là tia đối của tia \(BC.\)
Vì \(\widehat {C'BA'}\) kề bù với \(\widehat {ABC'}\) nên tia \(BA'\) là tia đối của tia \(BA.\)
Do đó \(\widehat {C'BA'}\) và \(\widehat {CBA}\) là hai góc đối đỉnh.
\( \Rightarrow \widehat {C'BA'} = \widehat {CBA} = {62^0}\) (tính chất hai góc đối đỉnh).
Hướng dẫn giải:
+ Áp dụng tính chất hai góc kề bù để xác định các tia đối nhau, từ đó xác định góc đối đỉnh với góc \(C'BA'\).
+ Áp dụng tính chất hai góc đối đỉnh để tính góc \(C'BA'\): “Hai góc đối đỉnh thì bằng nhau”.