Câu hỏi:
2 năm trước
Cho hai đường thẳng \(xx'\) và \(yy'\) giao nhau tại \(O\) sao cho \(\widehat {x'Oy} = 55^\circ \). Chọn câu sai.
Trả lời bởi giáo viên
Đáp án đúng: b
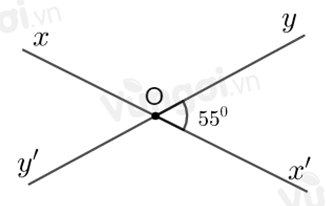
Vì hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) nên hai tia \(Ox\) và \(Ox'\) là hai tia đối nhau; hai tia \(Oy\) và \(Oy'\) là hai tia đối nhau.
Suy ra \(\widehat {xOy}\) và \(\widehat {x'Oy'}\); \(\widehat {x'Oy}\) và \(\widehat {xOy'}\) là hai cặp góc đối đỉnh.
Do đó \(\widehat {xOy'} = \widehat {x'Oy} = {55^0}\) và \(\widehat {x'Oy'} = \widehat {xOy}\)
Lại có: \(\widehat {xOy}\) và \(\widehat {x'Oy}\) là hai góc kề bù nên \(\widehat {xOy} + \widehat {x'Oy} = 180^\circ \)
\( \Rightarrow \widehat {xOy} + {55^0} = {180^0}\)
\( \Rightarrow \widehat {xOy} = {180^0} - {55^0} = {125^0}\)
Vậy \(\widehat {xOy'} = \widehat {x'Oy} = {55^0}\) và \(\widehat {x'Oy'} = \widehat {xOy} = {125^0}\)
Suy ra A, C, D đúng, B sai.
Hướng dẫn giải:
+ Sử dụng tính chất: Hai góc đối đỉnh thì bằng nhau.
+ Sử dụng: Hai góc kề bù có tổng bằng \({180^0}.\)
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
