Cho hình vẽ sau. Chọn phát biểu đúng.
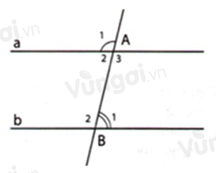

\(\widehat {\;{A_1}}\) và \(\widehat {\;{B_2}}\) là hai góc so le trong (sai, vì đó là hai góc đồng vị, loại đáp án A)
\(\widehat {\;\;{A_2}}\) và \(\widehat {\;{B_1}}\) là hai góc so le trong (đúng, chọn B)
\(\widehat {\;{A_3}}\) và \(\widehat {{B_1}}\) là hai góc đồng vị (sai, vì đó là hai góc trong cùng phía, loại đáp án C)
\(\widehat {\;{A_3}}\) và \(\widehat {\;{B_2}}\) là hai góc trong cùng phía (sai, vì đó là hai góc so le trong, loại đáp án D)
Chọn một cặp góc trong cùng phía trong hình vẽ sau:


Ta có:
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\) là hai góc so le ngoài nên đáp án A sai.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\) là hai góc so le trong nên đáp án B sai.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) là hai góc trong cùng phía nên đáp án C đúng.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị nên đáp án D sai.
Chọn một cặp góc trong cùng phía trong hình vẽ sau:


\(\widehat {BCA}\) và \(\widehat {CAD}\) là hai góc trong cùng phía (sai, vì đây là 2 góc so le trong), loại A.
\(\widehat {CEF}\) và \(\widehat {EAD}\) là hai góc trong cùng phía (sai, vì đây là 2 góc đồng vị), loại B.
\(\widehat {CFE}\) và \(\widehat {FDA}\) là hai góc trong cùng phía (sai, vì đây là 2 góc đồng vị), loại C.
\(\widehat {CFE}\) và \(\widehat {CEF}\) là hai góc trong cùng phía (đúng), chọn D.
Nếu đường thẳng \(c\) cắt hai đường thẳng \(a,\,b\) và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì:
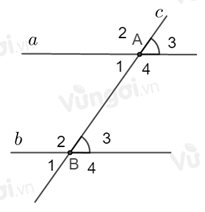
Đường thẳng \(c\) cắt hai đường thẳng \(a,b\) tương ứng tại \(A,B\) và trong các góc tạo thành có một cặp góc đồng vị bằng nhau, giả sử \(\widehat {{A_3}} = \widehat {{B_3}}\)
+ Xét một cặp góc trong cùng phía, chẳng hạn \(\widehat {{A_4}};\,\widehat {{B_3}}\)
Ta có: \(\widehat {{A_4}} + \,\widehat {{B_3}} = \widehat {{A_4}} + \widehat {{A_3}}\) (do \(\widehat {{A_3}} = \widehat {{B_3}}\))
Lại có: \(\widehat {{A_4}};\widehat {{A_3}}\) là hai góc kề bù nên \(\widehat {{A_4}} + \widehat {{A_3}} = {180^0}\)
Suy ra \(\widehat {{A_4}} + \widehat {{B_3}} = {180^0}\). Do đó hai góc trong cùng phía bù nhau nên A sai, C đúng.
+ Xét một cặp góc so le trong, chẳng hạn \(\widehat {{A_1}};\,\widehat {{B_3}}\)
Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (hai góc đối đỉnh)
Mà \(\widehat {{A_3}} = \widehat {{B_3}}\) nên \(\widehat {{A_1}} = \widehat {{B_3}}\).
Vậy hai góc so le trong bằng nhau. Đáp án B sai.
Cho hình vẽ sau:

Có bao nhiêu cặp góc trong cùng phía?
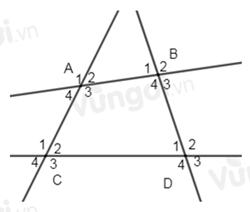
Các cặp góc trong cùng phía là: \(\widehat {{A_4}}\) và \(\widehat {{C_1}}\); \(\widehat {{A_3}}\) và \(\widehat {{C_2}}\); \(\widehat {{B_4}}\) và \(\widehat {{D_1}}\); \(\widehat {{B_3}}\) và \(\widehat {{D_2}}\); \(\widehat {{A_2}}\) và \(\widehat {{B_1}}\); \(\widehat {{A_3}}\) và \(\widehat {{B_4}}\); \(\widehat {{C_2}}\) và \(\widehat {{D_1}}\);
\(\widehat {{C_3}}\) và \(\widehat {{D_4}}\).
Vậy có \(8\) cặp góc trong cùng phía.
Cho hình vẽ:
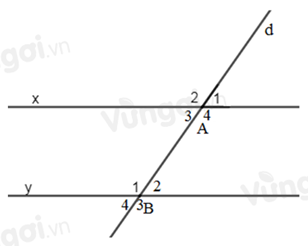
Biết một cặp góc so le trong \(\widehat {{A_4}} = \widehat {{B_1}} = {130^0}\). Tính số đo của cặp góc so le trong còn lại.

Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (hai góc kề bù)
\( \Rightarrow \widehat {{A_3}} = {180^0} - \widehat {{A_4}} = {180^0} - {130^0} = {50^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng \(d\) cắt 2 đường thẳng \(x,y\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (\(\widehat {{A_4}} = \widehat {{B_1}} = {130^0}\))
Do đó \(\widehat {{B_2}} = \widehat {{A_3}} = {50^0}.\)
Cho hình vẽ sau:

Biết \(\widehat {{M_1}} = \widehat {{N_1}} = {35^0}.\) Tính \(\widehat {{M_4}} + \widehat {{N_3}},\,\widehat {{M_2}} + \widehat {{N_1}}.\)
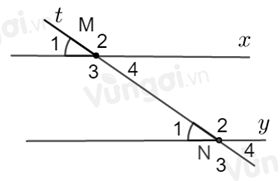
+ Ta có: \(\widehat {{M_4}};\widehat {{M_1}}\) là hai góc đối đỉnh nên \(\widehat {{M_4}} = \widehat {{M_1}} = {35^0}\) (tính chất hai góc đối đỉnh)
Lại có: \(\widehat {{N_1}};\widehat {{N_3}}\) là hai góc kề bù nên \(\widehat {{N_1}} + \widehat {{N_3}} = {180^0}\) \( \Rightarrow \widehat {{N_3}} = {180^0} - \widehat {{N_1}}\) \( \Rightarrow \widehat {{N_3}} = {180^0} - {35^0} = {145^0}\)
Vậy \(\widehat {{M_4}} + \widehat {{N_3}} = {35^0} + {145^0} = {180^0}\)
+ Ta có: \(\widehat {{M_1}};\widehat {{M_2}}\) là hai góc kề bù nên \(\widehat {{M_1}} + \widehat {{M_2}} = {180^0}\) \( \Rightarrow \widehat {{M_2}} = {180^0} - \widehat {{M_1}}\) \( \Rightarrow \widehat {{M_2}} = {180^0} - {35^0} = {145^0}\)
Vậy \(\,\widehat {{M_2}} + \widehat {{N_1}} = {145^0} + {35^0} = {180^0}\)
Tính giá trị \(x;y;z;t\) trên hình sau:

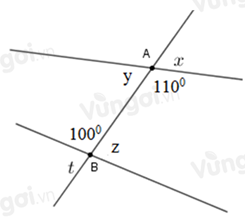
Ta có: \(y + {110^0} = {180^0}\) (hai góc kề bù) \( \Rightarrow y = {180^0} - {110^0} = {70^0}\)
\(x = y = {70^0}\) (tính chất hai góc đối đỉnh)
Tương tự ta có: \(z + {100^0} = {180^0}\) (hai góc kề bù) \( \Rightarrow z = {180^0} - {100^0} = {80^0}\)
\(t = z = {80^0}\) (tính chất hai góc đối đỉnh)
Vậy \(x = {70^0};y = {70^0};z = {80^0};t = {80^0}\).
Cho hình vẽ sau:
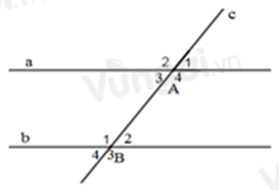
Biết \(\widehat {{A_4}} = {110^0};\widehat {{B_2}} = {70^0}\). Tính số đo góc \({B_4}\) và góc \({A_3}.\)

Ta có: \(\widehat {{A_3}};\widehat {{A_4}}\) là hai góc kề bù nên \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) \( \Rightarrow \widehat {{A_3}} = {180^0} - \widehat {{A_4}}\) \( \Rightarrow \widehat {{A_3}} = {180^0} - {110^0} = {70^0}\)
Vì \(\widehat {{B_2}};\widehat {{B_4}}\) là hai góc đối đỉnh nên \(\widehat {{B_4}} = \widehat {{B_2}} = {70^0}\) (tính chất hai góc đối đỉnh)
Vậy \(\widehat {{B_4}} = \widehat {{A_3}} = {70^0}\).
Cho hình vẽ sau:
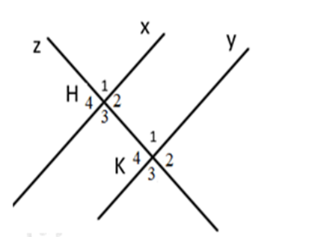
Chọn phát biểu đúng.
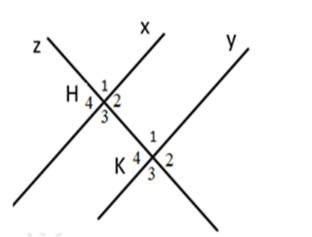
\(\widehat {{H_1}}\) và \(\widehat {{K_1}}\) là hai góc so le trong (sai, vì đó là 2 góc đồng vị, loại đáp án A)
\(\widehat {{H_4}}\) và \(\widehat {{K_4}}\) là hai góc đồng vị (đúng, chọn B)
\(\widehat {{H_3}}\) và \(\widehat {{K_4}}\) là hai góc so le ngoài (sai, vì đó là 2 góc trong cùng phía, loại đáp án C)
\(\widehat {{H_4}}\) và \(\widehat {{K_2}}\) là hai góc so le trong (sai, vì đó là 2 góc so le ngoài, loại đáp án D)
Chọn một cặp góc đồng vị trong hình vẽ sau:
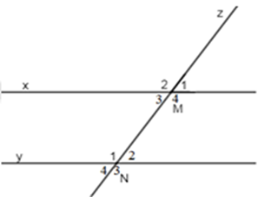
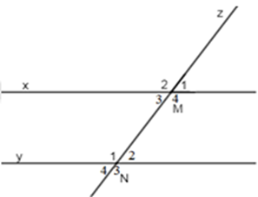
\(\widehat {{M_1}}\) và \(\widehat {{N_4}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le ngoài) loại đáp án A.
\(\widehat {{M_3}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc so le trong) loại đáp án B.
\(\widehat {{M_4}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (sai, vì đó là là hai góc trong cùng phía) loại đáp án C.
\(\widehat {{M_1}}\) và \(\widehat {{N_2}}\) là hai góc đồng vị (đúng) chọn đáp án D.
Chọn một cặp góc so le trong trong hình vẽ sau:
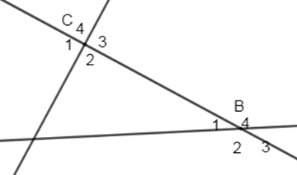
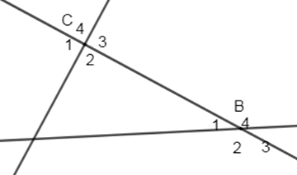
\(\widehat {{C_3}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (đúng) chọn A
\(\widehat {{C_1}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (sai, vì đây là 2 góc đồng vị), loại B
\(\widehat {{C_4}}\) và \(\widehat {{B_4}}\) là hai góc so le trong (sai, vì đây là 2 góc đồng vị), loại C
\(\widehat {{C_2}}\) và \(\widehat {{B_1}}\) là hai góc so le trong (sai, vì đây là 2 góc trong cùng phía), loại D.
Nếu đường thẳng c cắt hai đường thẳng a, b và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
Nếu đường thẳng $c$ cắt hai đường thẳng $a,b$ và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì: hai góc đồng vị bằng nhau
Cho hình vẽ sau:
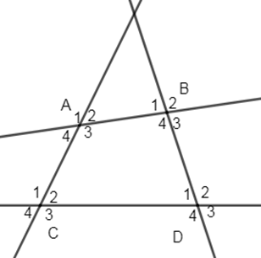
Có bao nhiêu cặp góc đồng vị?
Các cặp góc đồng vị là: \(\widehat {{A_1}}\) và \(\widehat {{C_1}}\), \(\widehat {{A_4}}\) và \(\widehat {{C_4}}\), \(\widehat {{A_2}}\) và \(\widehat {{C_2}}\), \(\widehat {{A_3}}\) và \(\widehat {{C_3}}\), \(\widehat {{B_1}}\) và \(\widehat {{D_1}}\), \(\widehat {{B_2}}\) và \(\widehat {{D_2}}\), \(\widehat {{B_3}}\) và \(\widehat {{D_3}}\), \(\widehat {{B_4}}\) và \(\widehat {{D_4}}\).
Tương tự ta có thêm $8$ cặp góc đồng vị \(\widehat {{A_1}}\) và \(\widehat {{B_1}}\), \(\widehat {{A_4}}\) và \(\widehat {{B_4}}\), \(\widehat {{A_2}}\) và \(\widehat {{B_2}}\), \(\widehat {{A_3}}\) và \(\widehat {{B_3}}\), \(\widehat {{C_1}}\) và \(\widehat {{D_1}}\), \(\widehat {{C_2}}\) và \(\widehat {{D_2}}\), \(\widehat {{C_3}}\) và \(\widehat {{D_3}}\), \(\widehat {{C_4}}\) và \(\widehat {{D_4}}\).
Biết một cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\). Tính số đo của cặp góc so le trong còn lại.
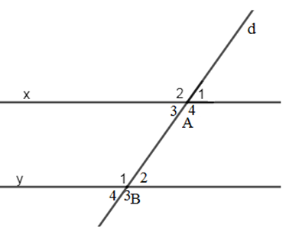
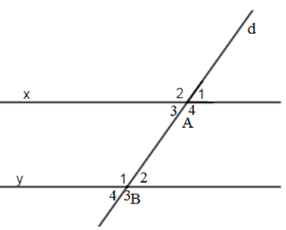
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\( \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {35^0} = {145^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng d cắt 2 đường thẳng x và y tạo thành 1
cặp góc so le trong \(\widehat {{A_3}} = \widehat {{B_2}} = {35^0}\)nên \( \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {145^0}.\)
Cho hình vẽ sau:
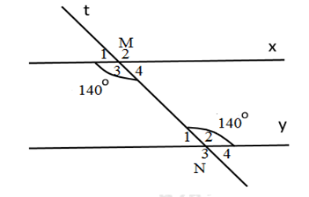
Biết \(\widehat {{M_3}} = \widehat {{N_2}} = {140^0}.\) Tính \(\widehat {{M_4}} + \widehat {{N_2}},\,\widehat {{M_3}} + \widehat {{N_1}}.\)
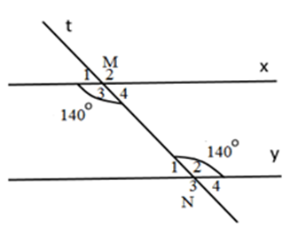
Ta có: \(\widehat {{M_3}} + \widehat {{M_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{M_4}} = {180^0} - \widehat {{M_3}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_4}} + \,\widehat {{N_2}} = {40^0} + {140^0} = {180^0}\end{array}\)
Ta có: \(\widehat {{N_2}} + \widehat {{N_1}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{N_1}} = {180^0} - \widehat {{N_2}} = {180^0} - {140^0} = {40^0}\\ \Rightarrow \widehat {{M_3}} + \widehat {{N_1}} = {140^0} + {40^0} = {180^0}\end{array}\)
Cho hình vẽ sau:
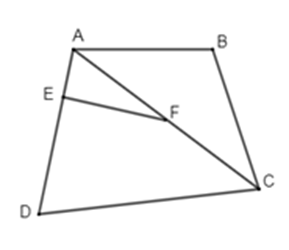
Em hãy chọn câu đúng nhất trong các câu sau:
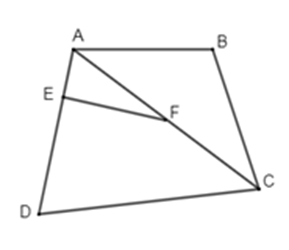
- \(\widehat {AEF}\) và \(\widehat {A{\rm{D}}C}\) là hai góc đồng vị (đúng, chọn A)
- $\widehat {AFE}$ và \(\widehat {BAC}\) là hai góc trong cùng phía (sai, vì đó là hai góc so le trong) loại B
- \(\widehat {DCA}\) và $\widehat {AFE}$ là hai góc so le trong (sai, vì đó là hai góc đồng vị) loại C
- \(\widehat {BAC}\) và \(\widehat {DCA}\) là hai góc đồng vị (sai, vì đó là hai góc so le trong) loại D
Tính giá trị \(x;y;z;t\) trên hình sau:
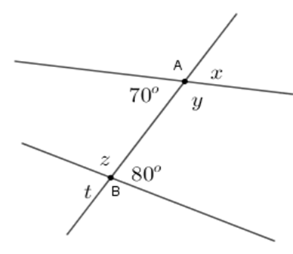
Ta có \(x = {70^0}\) (tính chất hai góc đối đỉnh)
\(y + {70^o} = {180^o} \Rightarrow y = {110^o}\) (hai góc kề bù)
Tương tự ta có \(t = {80^o};\,z = {100^o}\)
Vậy $x = {70^o};y = {110^0};z = {100^o};t = {80^o}.$
Cho hình vẽ sau:
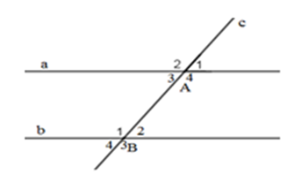
Biết \(\widehat {{A_3}} = \widehat {{B_2}} = {30^0}\). Tính số đo góc \({A_4}\) và góc \({B_1}.\)
Cặp góc so le trong còn lại là: \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\).
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{A_4}} = {180^0} - \widehat {{A_3}} = {180^0} - {30^0} = {150^0}\\ \Rightarrow \widehat {{A_4}} = \widehat {{B_1}} = {150^0}\end{array}\)
Trong hình dưới đây cho biết \(\widehat {{M_4}} = \widehat {{N_2}} = {100^0}\). Tính các góc tại đỉnh \(M,N.\)
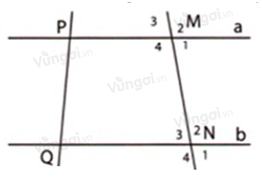
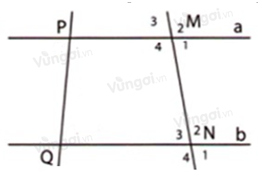
+ Tại \(M\):
Vì \(\widehat {{M_2}};\widehat {{M_4}}\) là hai góc đối đỉnh nên \(\widehat {{M_2}} = \widehat {{M_4}} = {100^0}\) (tính chất hai góc đối đỉnh)
Ta có: \(\widehat {{M_4}};\widehat {{M_1}}\) là hai góc kề bù nên \(\widehat {{M_4}} + \widehat {{M_1}} = {180^0}\) \( \Rightarrow \widehat {{M_1}} = {180^0} - \widehat {{M_4}} = {180^0} - {100^0} = {80^0}\)
Vì \(\widehat {{M_3}};\widehat {{M_1}}\) là hai góc đối đỉnh nên \(\widehat {{M_3}} = \widehat {{M_1}} = {80^0}\) (tính chất hai góc đối đỉnh)
+ Tại \(N\):
Vì \(\widehat {{N_2}};\widehat {{N_4}}\) là hai góc đối đỉnh nên \(\widehat {{N_4}} = \widehat {{N_2}} = {100^0}\) (tính chất hai góc đối đỉnh)
Ta có: \(\widehat {{N_2}};\widehat {{N_3}}\) là hai góc kề bù nên \(\widehat {{N_2}} + \widehat {{N_3}} = {180^0}\) \( \Rightarrow \widehat {{N_3}} = {180^0} - \widehat {{N_2}} = {180^0} - {100^0} = {80^0}\)
Vì \(\widehat {{N_3}};\widehat {{N_1}}\) là hai góc đối đỉnh nên \(\widehat {{N_3}} = \widehat {{N_1}} = {80^0}\) (tính chất hai góc đối đỉnh)
Vậy \(\widehat {{M_1}} = \widehat {{M_3}} = \widehat {{N_1}} = \widehat {{N_3}} = {80^0};\widehat {{M_2}} = \widehat {{N_4}} = {100^0}\).

