Câu hỏi:
2 năm trước
Cho hình vẽ:
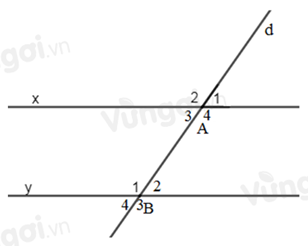
Biết một cặp góc so le trong \(\widehat {{A_4}} = \widehat {{B_1}} = {130^0}\). Tính số đo của cặp góc so le trong còn lại.
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \(\widehat {{A_3}} + \widehat {{A_4}} = {180^0}\) (hai góc kề bù)
\( \Rightarrow \widehat {{A_3}} = {180^0} - \widehat {{A_4}} = {180^0} - {130^0} = {50^0}\)
Ta có: \(\widehat {{A_3}}\) và \(\widehat {{B_2}}\); \(\widehat {{A_4}}\) và \(\widehat {{B_1}}\) là 2 cặp góc so le trong
Mặt khác, đường thẳng \(d\) cắt 2 đường thẳng \(x,y\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (\(\widehat {{A_4}} = \widehat {{B_1}} = {130^0}\))
Do đó \(\widehat {{B_2}} = \widehat {{A_3}} = {50^0}.\)
Hướng dẫn giải:
+ Sử dụng: “Hai góc kề bù có tổng bằng \({180^0}\)” để tính \(\widehat {{A_3}}\)
+ Áp dụng tính chất: “Nếu đường thẳng \(c\) cắt hai đường thẳng \(a,b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau thì hai góc so le trong còn lại bằng nhau” để tính góc \(\widehat {{B_2}}\).
Câu hỏi khác
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
