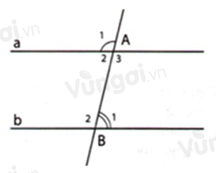
Nếu đường thẳng \(c\) cắt hai đường thẳng \(a,\,b\) và trong các góc tạo thành có một cặp góc đồng vị bằng nhau thì:

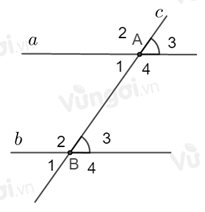
Đường thẳng \(c\) cắt hai đường thẳng \(a,b\) tương ứng tại \(A,B\) và trong các góc tạo thành có một cặp góc đồng vị bằng nhau, giả sử \(\widehat {{A_3}} = \widehat {{B_3}}\)

+ Xét một cặp góc trong cùng phía, chẳng hạn \(\widehat {{A_4}};\,\widehat {{B_3}}\)

Ta có: \(\widehat {{A_4}} + \,\widehat {{B_3}} = \widehat {{A_4}} + \widehat {{A_3}}\) (do \(\widehat {{A_3}} = \widehat {{B_3}}\))

Lại có: \(\widehat {{A_4}};\widehat {{A_3}}\) là hai góc kề bù nên \(\widehat {{A_4}} + \widehat {{A_3}} = {180^0}\)

Suy ra \(\widehat {{A_4}} + \widehat {{B_3}} = {180^0}\). Do đó hai góc trong cùng phía bù nhau nên A sai, C đúng.
+ Xét một cặp góc so le trong, chẳng hạn \(\widehat {{A_1}};\,\widehat {{B_3}}\)

Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (hai góc đối đỉnh)

Mà \(\widehat {{A_3}} = \widehat {{B_3}}\) nên \(\widehat {{A_1}} = \widehat {{B_3}}\).

Vậy hai góc so le trong bằng nhau. Đáp án B sai.