Cho ba đường thẳng phân biệt \(a,\,b\) và c, biết \(a \bot b\) và \(a \bot c\). Kết luận nào đúng:
Ta có: \(\left\{ \begin{array}{l}a \bot b\\a\, \bot c\end{array} \right. \Rightarrow \,b//c\) (quan hệ giữa tính vuông góc với tính song song)
Điền cụm từ thích hợp vào chỗ trống: Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng …
Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
Cho hình vẽ sau:
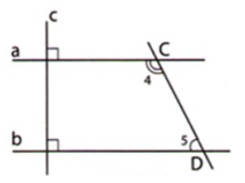
Biết \(a \bot c,\,b \bot c,\,\widehat {{D_5}} = {64^0}\). Tính \(\widehat {{C_4}}\).
Vì \(\left\{ \begin{array}{l}a \bot c\\b \bot c\end{array} \right. \Rightarrow a\,//\,b\) (quan hệ giữa tính vuông góc với tính song song)
Vì \(a//b\) nên \(\widehat {{C_4}} + \widehat {{D_5}} = {180^o}\) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {{C_4}} = {180^o} - \widehat {{D_5}} = {180^o} - {64^o} = {116^o}\)
Cho hai đường thẳng \(a\) và \(b\) cùng vuông góc với đường thẳng \(c,\) \(c\) vuông góc với \(a\) tại \(M\) và vuông góc với \(b\) tại \(N.\) Một đường thẳng \(m\) cắt \(a,b\) tại \(A,B.\) Biết \(\widehat {ABN} = 2\widehat {MAB}\). Số đo góc \(MAB\) là:

Từ đề bài ta có: \(a \bot c;b \bot c\) suy ra \(a//b\) (quan hệ từ vuông góc đến song song)
Vì \(a//b\,\,(cmt)\) nên \(\widehat {ABN} + \widehat {MAB} = 180^\circ \) (hai góc trong cùng phía bù nhau).
Mà \(\widehat {ABN} = 2\widehat {MAB}\) nên \(2\widehat {MAB} + \widehat {MAB} = 180^\circ \Rightarrow 3\widehat {MAB} = {180^o} \Rightarrow \widehat {MAB} = {180^o}:3 = {60^o}.\)
Vậy \(\widehat {MAB} = 60^\circ .\)
Cho hình vẽ sau:

Biết \(AD//\,BC,\,\widehat {BA{\rm{D}}} = {110^0};\,AD \bot DC\). Số đo góc $ABC$ là:
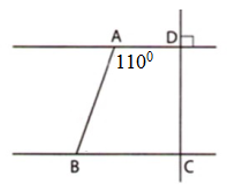
Ta có: \(\left\{ \begin{array}{l}AD\,//\,BC\\AD \bot DC\end{array} \right. \Rightarrow BC \bot DC\) (quan hệ giữa tính vuông góc với tính song song)
Theo đề bài: \(AD//\,BC \Rightarrow \widehat {DAB} + \widehat {ABC} = {180^0}\) (2 góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {ABC} = {180^0} - {110^0} = {70^0}\).
Cho hình vẽ sau:

Biết \(AB \bot a,\,AB \bot b,\,\widehat {aHI} = {140^0}\). Tính \(\widehat {IFB}\).

Ta có: \(\left\{ \begin{array}{l}AB \bot a\\AB \bot b\end{array} \right. \Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song)
Vì \(a//b\,\,(cmt)\) nên \(\widehat {aHI} + \widehat {IFB} = {180^o}\) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {IFB} = {180^o} - \widehat {aHI} = {180^o} - {140^o} = {40^o}.\)
Cho hình vẽ sau. Tính số đo góc \(ADC.\)


Ta có: \(AB \bot BC;DC \bot BC\) \( \Rightarrow AB//DC\) (quan hệ từ vuông góc đến song song)
Suy ra \(\widehat {ADC} + \widehat {BAD} = 180^\circ \) (hai góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {ADC} = 180^\circ - \widehat {BAD} = 180^\circ - 100^\circ = 80^\circ \)
Vậy \(\widehat {ADC} = 80^\circ .\)
Cho hình vẽ sau:
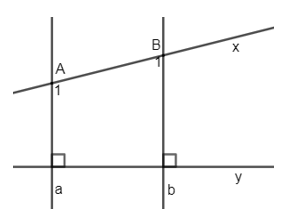
Biết \(a \bot y,\,b \bot y,\,\widehat {{A_1}} - \widehat {{B_1}} = {36^0}\). Tính \(\widehat {{A_1}}\).
Theo đề bài ta có: \(a \bot y,\,b \bot y \Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song)
\( \Rightarrow \widehat {{A_1}} + \widehat {{B_1}} = {180^0}\) (2 góc trong cùng phía bù nhau).
Lại có: \(\widehat {{A_1}} - \widehat {{B_1}} = {36^0}\left( {gt} \right) \Rightarrow \widehat {{A_1}} = \left( {{{180}^0} + {{36}^0}} \right):2 = {108^0}\).
Cho hình vẽ sau biết \(AB//DE.\) Tính \(\widehat {ACD}.\)
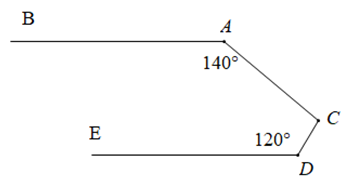

Trong \(\widehat {ACD}\) vẽ tia \(CF\) song song với \(AB\).
Vì \(AB//\,CF\) (theo cách vẽ) nên \(\widehat {BAC} + \widehat {{C_1}} = {180^o}\) (2 góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {{C_1}} = {180^o} - \widehat {BAC} = {180^o} - {140^o} = {40^o}.\)
Theo đề bài ta có: \(AB//DE\) và \(CF//AB\) (theo cách vẽ) nên \(CF//DE\)
Vì \(CF//DE\) nên \(\widehat {{C_2}} + \widehat {CDE} = {180^o}\) (2 góc trong cùng phía bù nhau).
\( \Rightarrow \widehat {{C_2}} = {180^o} - \widehat {CDE} = {180^o} - {120^o} = {60^o}.\)
Vì tia \(CF\) nằm trong \(\widehat {ACD}\) nên tia \(CF\) nằm giữa hai tia \(CA\) và tia \(CD\), ta có:
\(\widehat {ACD} = \widehat {{C_1}} + \widehat {{C_2}} = {40^o} + {60^o} = {100^o}.\)
Cho hình vẽ sau, biết \(AB//DE\), tính \(\widehat {BCE}.\)
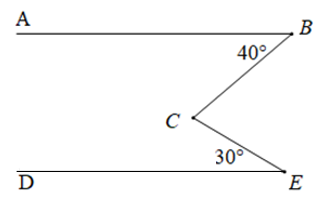
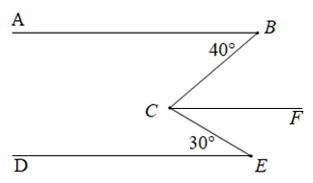
Trong \(\widehat {BCE}\) vẽ tia \(CF\) song song với \(AB\).
Vì \(AB//CF\) (theo cách vẽ) nên \(\widehat {ABC} = \widehat {BCF} = {40^o}\) (hai góc so le trong bằng nhau).
Theo đề bài: \(AB//DE\) và \(AB//CF\) (theo cách dựng) nên \(CF//DE\).
Vì \(CF//DE\,(cmt)\) nên \(\widehat {FCE} = \widehat {CED} = {30^o}\) (hai góc so le trong bằng nhau).
Vì tia \(CF\) nằm trong \(\widehat {BCE}\) (theo cách vẽ) nên tia \(CF\) nằm giữa hai tia \(CB\) và tia \(CE\), ta có:
\(\widehat {BCE} = \widehat {BCF} + \widehat {FCE} = {40^o} + {30^o} = {70^o}.\)
Cho hình vẽ sau, biết \(\widehat {MNO} = \alpha ,\widehat {OPQ} = \beta \) và \(\widehat {NOP} = \alpha + \beta \,\left( {{0^0} < \alpha ;\beta < {{90}^0}} \right)\). Chọn câu đúng.


Trong \(\widehat {NOP}\) vẽ tia \(Ox\) song song với \(MN.\)
Vì \(MN//Ox\) (theo cách vẽ) nên \(\widehat {MNO} = \widehat {NOx} = \alpha \) (hai góc so le trong bằng nhau).
Vì \(Ox\) nằm trong \(\widehat {NOP}\) nên tia \(Ox\) nằm giữa hai tia \(ON,\,OP\) do đó ta có:
\(\begin{array}{l}\widehat {NOP} = \widehat {NOx} + \widehat {xOP}\\ \Rightarrow \widehat {xOP} = \widehat {NOP} - \widehat {NOx} = \left( {\alpha + \beta } \right) - \alpha = \beta \end{array}\)
Ta có: \(\widehat {xOP} = \widehat {OPQ} = \beta \) mà \(\widehat {xOP}\) và \(\widehat {OPQ}\) ở vị trí so le trong nên \(Ox//PQ\).
\(MN//Ox\) (theo cách vẽ) và \(Ox//PQ\,(cmt)\) nên \(MN//PQ.\)
Cho ba đường thẳng phân biệt \(a,\,b\) và c, biết \(a//b\) và \(a \bot c\). Kết luận nào đúng:
Ta có: \(\left\{ \begin{array}{l}a//b\\a\, \bot c\end{array} \right. \Rightarrow \,b \bot c\) (quan hệ giữa tính vuông góc với tính song song)
Cho ba đường thẳng phân biệt a, b, c, biết \(a//b\) và \(b//c\) . Chọn kết luận đúng:
Ta có: \(\left\{ \begin{array}{l}a//c\\b//c\end{array} \right. \Rightarrow a//\,b\) (hai đường thẳng cùng cùng song song với một đường thẳng thứ ba thì song song với nhau)
Cho hình vẽ sau:
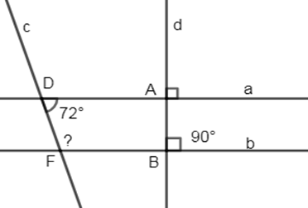
Biết \(a \bot d,\,b \bot d,\,\widehat {A{\rm{D}}F} = {72^0}\). Tính \(\widehat {DFB}\).
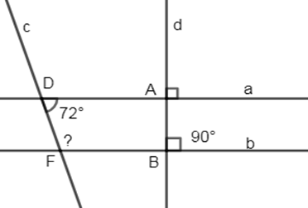
Vì \(\left\{ \begin{array}{l}a \bot d\\b \bot d\end{array} \right. \Rightarrow a\,//\,b\) (quan hệ giữa tính vuông góc với tính song song)
\( \Rightarrow \widehat {ADF} + \widehat {DFB} = {180^0} \)(2 góc trong cùng phía bù nhau)
\(\Rightarrow \widehat {DFB} = {180^0} - \widehat {ADF}\) \( = {180^0} - {72^0} = {108^0}\)
Cho hai đường thẳng $a$ và $b$ cùng vuông góc với đường thẳng $c,$ $c$ vuông góc với $a$ tại $M$ và vuông góc với $b$ tại $N.$ Một đường thẳng $m$ cắt $a,b$ tại $A,B.$ Biết \(\widehat {ABN} - \widehat {MAB} = 40^\circ \). Số đo góc $BAM$ là:
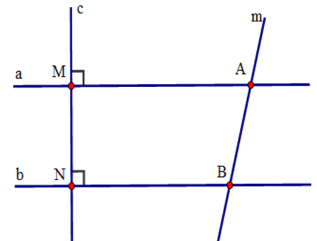
Từ đề bài ta có \(a \bot c;b \bot c \Rightarrow a//b\) (quan hệ từ vuông góc đến song song)
Suy ra \(\widehat {ABN} + \widehat {MAB} = 180^\circ \) (hai góc trong cùng phía bù nhau)
mà \(\widehat {ABN} - \widehat {MAB} = 40^\circ \)
nên \(\widehat {ABN} = \dfrac{{180^\circ + 40^\circ }}{2} = 110^\circ \) và \(\widehat {MAB} = 180^\circ - \widehat {ABN} \)\(= 180^\circ - 110^\circ = 70^\circ \)
Vậy \(\widehat {BAM} = 70^\circ .\)
Cho hình vẽ sau:
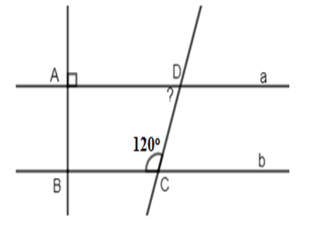
Biết \(a//\,b,\,\widehat {BC{\rm{D}}} = {120^0}\) và $a \bot AB$. Kết luận nào sau đây là đúng:
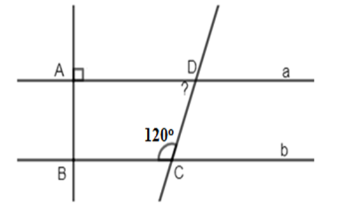
Ta có: \(\left\{ \begin{array}{l}a\,//\,b\\AB \bot a\end{array} \right. \Rightarrow AB \bot b\) (quan hệ giữa tính vuông góc với tính song song)
Vì \(a//\,b\left( {gt} \right) \Rightarrow \widehat {A{\rm{D}}C} + \widehat {BC{\rm{D}}} = {180^0}\) (2 góc trong cùng phía bù nhau)
\( \Rightarrow \widehat {A{\rm{D}}C} = {180^0} - \widehat {BC{\rm{D}}} = {180^0} - {120^0} = {60^0}\)
Cho hình vẽ sau:
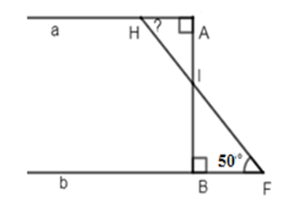
Biết \(AB \bot a,\,AB \bot b,\,\widehat {BFH} = {50^0}\). Tính \(\widehat {AHF}\).
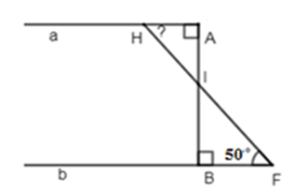
Ta có: \(\left\{ \begin{array}{l}AB \bot a\\AB \bot b\end{array} \right. \Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song)
\( \Rightarrow \widehat {BFH} = \widehat {AHF} = {50^0}\) (so le trong)
Cho hình vẽ sau. Tính số đo góc \(BAD.\)
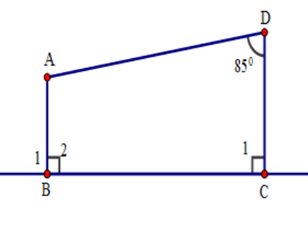
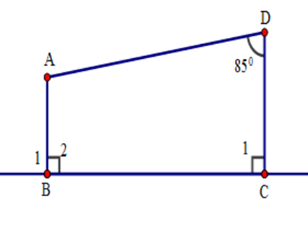
Ta thấy \(AB \bot BC;DC \bot BC\) \( \Rightarrow AB//DC\) (quan hệ từ vuông góc đến song song)
Suy ra \(\widehat {ADC} + \widehat {BAD} = 180^\circ \) (hai góc trong cùng phía bù nhau)
\( \Rightarrow \widehat {BAD} = 180^\circ - \widehat {ADC} = 180^\circ - 85^\circ = 95^\circ \)
Vậy \(\widehat {BAD} = 95^\circ .\)
Cho hình vẽ sau:
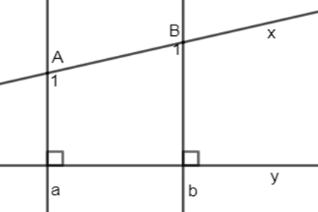
Biết \(a \bot y,\,b \bot y,\,\widehat {{A_1}} - \widehat {{B_1}} = {40^0}\). Tính \(\widehat {{B_1}}\).
Ta có: \(\left\{ \begin{array}{l}a \bot y\\b \bot y\end{array} \right.\left( {gt} \right) \Rightarrow a//\,b\) (quan hệ giữa tính vuông góc với tính song song)
\( \Rightarrow \widehat {{A_1}} + \widehat {{B_1}} = {180^0}\) (2 góc trong cùng phía bù nhau)
Lại có: \(\widehat {{A_1}} - \widehat {{B_1}} = {40^0}\left( {gt} \right) \Rightarrow \widehat {{B_1}} = \left( {{{180}^0} - {{40}^0}} \right):2 = {70^0}\)
Cho hình vẽ sau biết $AD//BC.$ Tính \(\widehat {AGB}.\)
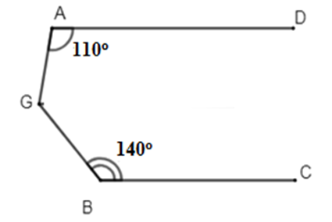
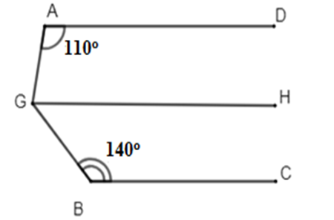
Qua \(G\) kẻ \(GH//AD.\)
Vì \(A{\rm{D}}//\,GH \Rightarrow \widehat {GA{\rm{D}}} + \widehat {AGH} = {180^0} \Rightarrow \widehat {AGH} = {180^0} - \widehat {GA{\rm{D}}} = {180^0} - {110^0} = {70^0}\) (2 góc trong cùng phía bù nhau)
Ta có: \(\left\{ \begin{array}{l}A{\rm{D}}//\,GH\\A{\rm{D}}//\,BC\end{array} \right.\left( {gt} \right) \Rightarrow GH//\,BC\)
\( \Rightarrow \widehat {HGB} + \widehat {GBC} = {180^0} \Rightarrow \widehat {HGB} = {180^0} - \widehat {GBC} = {180^0} - {140^0} = {40^0}\) (2 góc trong cùng phía bù nhau)
\(\widehat {AGB} = \widehat {AGH} + \widehat {HGB} = {70^0} + {40^0} = {110^0}\)

