Trả lời bởi giáo viên
Đáp án đúng: b
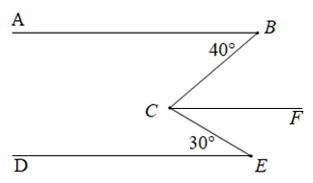
Trong \(\widehat {BCE}\) vẽ tia \(CF\) song song với \(AB\).
Vì \(AB//CF\) (theo cách vẽ) nên \(\widehat {ABC} = \widehat {BCF} = {40^o}\) (hai góc so le trong bằng nhau).
Theo đề bài: \(AB//DE\) và \(AB//CF\) (theo cách dựng) nên \(CF//DE\).
Vì \(CF//DE\,(cmt)\) nên \(\widehat {FCE} = \widehat {CED} = {30^o}\) (hai góc so le trong bằng nhau).
Vì tia \(CF\) nằm trong \(\widehat {BCE}\) (theo cách vẽ) nên tia \(CF\) nằm giữa hai tia \(CB\) và tia \(CE\), ta có:
\(\widehat {BCE} = \widehat {BCF} + \widehat {FCE} = {40^o} + {30^o} = {70^o}.\)
Hướng dẫn giải:
+ Áp dụng tính chất: Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
+ Dấu hiệu nhận biết hai đường thẳng song song.
Câu hỏi khác
- Bài tập hai đường thẳng song song. Tiên đề ơ-clit về hai đường thẳng song song toán 7 có lời giải
- Bài tập hai góc đối đỉnh toán 7 có lời giải
- Bài tập mối liên hệ từ vuông góc đến song song toán 7 có lời giải
- Bài tập hai đường thẳng vuông góc toán 7 có lời giải
- Bài tập các góc tạo bởi một đường thẳng cắt hai đường thẳng toán 7 có lời giải
