Cho hình vẽ sau:
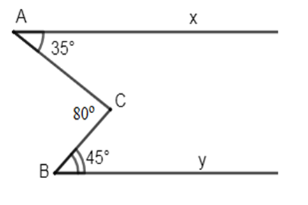
Biết \(\widehat {xAC} = {35^0},\,\widehat {CBy} = {45^0}\) và \(\widehat {ACB} = {80^0}.\) Khi đó chọn câu đúng.
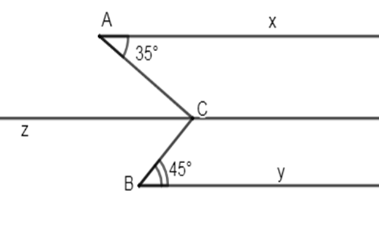
Kẻ \(Cz//{\rm{Ax}} \Rightarrow \widehat {xAC} = \widehat {ACz} = {35^0}\) (so le trong)
Ta có:
\(\widehat {ACz} + \widehat {zCB} = \widehat {ACB} \Rightarrow \widehat {zCB} = \widehat {ACB} - \widehat {ACz} = {80^0} - {35^0} = {45^0}\)
\( \Rightarrow \widehat {zCB} = \widehat {CBy}\left( { = {{45}^0}} \right)\)
Mà hai góc ở vị trí so le trong nên suy ra \(Cz//\,By\) (dấu hiệu nhận biết hai đường thẳng song song)
Ta có: \(\left\{ \begin{array}{l}Cz//\,Ax\left( {gt} \right)\\C{\rm{z}}//\,By\left( {cmt} \right)\end{array} \right. \Rightarrow Ax//\,By\) .
Cho hình vẽ sau
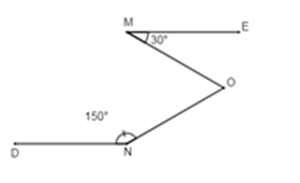
Biết \(ME//N{\rm{D}},\,\widehat {EM{\rm{O}}} = {30^0},\,\widehat {DNO} = {150^0}\). Tính \(\widehat {MON}\) .
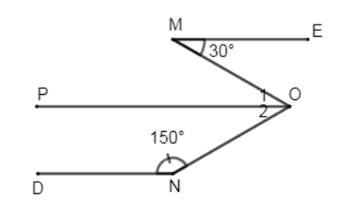
Kẻ \(OP\) sao cho \(OP//ME.\)
Ta có: \(OP//\,ME \Rightarrow \widehat M = \widehat {{O_1}} = {30^0}\) (2 góc so le trong)
Ta có: \(\left\{ \begin{array}{l}OP\,//\,ME\\ME\,//\,DN\end{array} \right.\left( {gt} \right) \Rightarrow PO\,//\,DN\)
\( \Rightarrow \widehat {{O_2}} + \widehat N = {180^0}\) (2 góc trong cùng phía bù nhau)
\( \Rightarrow \widehat {{O_2}} = {180^0} - \widehat N = {180^0} - {150^0} = {30^0}\)
Ta có: \(\widehat {MON} = \widehat {{O_1}} + \widehat {{O_2}} = {30^0} + {30^0} = {60^0}\)
Vậy \(\widehat {MON} = 60^\circ .\)

