Cho bảng giá trị sau. Chọn câu đúng.
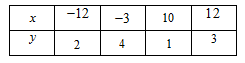
Từ bảng giá trị ta thấy với mỗi giá trị của $x$ ta luôn xác định được chỉ một giá trị tương ứng của $y$ nên đại lượng \(y\) là hàm số của đại lượng \(x.\)
Cho các công thức \(y - 3 = x;\, - 2y = x;\,{y^2} = x\). Có bao nhiêu công thức chứng tỏ rằng \(y\) là hàm số của $x$?
Nhận thấy \(y - 3 = x \Rightarrow y = x + 3\) là một hàm số
\( - 2y = x \Rightarrow y = - \dfrac{x}{2}\) là một hàm số
Với \({y^2} = x\) ta thấy khi \(x = 4\) thì \({y^2} = 4\) suy ra \(y = 2\) hoặc \(y = - 2\) nên với một giá trị của \(x\) cho hai giá trị của \(y\) nên \(y\) không là hàm số của \(x.\)
Cho hàm số \(y = f\left( x \right) = \dfrac{{15}}{{2x - 3}}\)
Tìm các giá trị của $x$ sao cho vế phải của công thức có nghĩa
Hàm số \(y = f\left( x \right) = \dfrac{{15}}{{2x - 3}}\) có nghĩa khi \(2x - 3 \ne 0 \Rightarrow 2x \ne 3 \Rightarrow x \ne \dfrac{3}{2}.\)
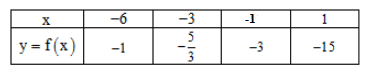
Cho hàm số \(y = f\left( x \right) = \dfrac{{15}}{{2x - 3}}\)
Bảng giá trị nào sau đây là đúng với hàm số \(y = f\left( x \right) = \dfrac{{15}}{{2x - 3}}\) ?
Tại \(x = - 6\) ta có \(f\left( { - 6} \right) = \dfrac{{15}}{{2.\left( { - 6} \right) - 3}} = - 1\)
Tại \(x = - 3\) thì \(f\left( { - 3} \right) = \dfrac{{15}}{{2.\left( { - 3} \right) - 3}} = \dfrac{{ - 15}}{9} = \dfrac{{ - 5}}{3}\)
Tại $x = - 1$ thì \(f\left( { - 1} \right) = \dfrac{{15}}{{2.\left( { - 1} \right) - 3}} = \dfrac{{ - 15}}{5} = - 3\)
Tại \(x = 1\) thì \(f\left( 1 \right) = \dfrac{{15}}{{2.1 - 3}} = - 15\)
Nên ta có bảng
Một hàm số được cho bằng công thức \(y = f\left( x \right) = - {x^2} + 2.\) Tính \(f\left( { - \dfrac{1}{2}} \right);f\left( 0 \right)\)
Ta có \(f\left( { - \dfrac{1}{2}} \right) \)\(= - {\left( { - \dfrac{1}{2}} \right)^2} + 2 \)\(= \dfrac{{ - 1}}{4} + 2 = \dfrac{7}{4}\)
\(f\left( 0 \right) = - {0^2} + 2 = 2\)
Vậy \(f\left( { - \dfrac{1}{2}} \right) = \dfrac{7}{4};f\left( 0 \right) = 2.\)
Một hàm số được cho bằng công thức \(y = f(x) = {x^2}.\) Tính \(f\left( { - 5} \right) + f\left( 5 \right)\)
Ta có \(f\left( { - 5} \right) = {\left( { - 5} \right)^2} = 25\) và \(f\left( 5 \right) = {5^2} = 25\)
Nên \(f\left( 5 \right) + f\left( { - 5} \right) = 25 + 25 = 50\)
Bảng giá trị nào sau đây là đúng với hàm số \(y = f\left( x \right) = \dfrac{{15}}{{2x - 3}}\) ?
Tại \(x = - 6\) ta có \(f\left( { - 6} \right) = \dfrac{{15}}{{2.\left( { - 6} \right) - 3}} = - 1\)
Tại \(x = - 3\) thì \(f\left( { - 3} \right) = \dfrac{{15}}{{2.\left( { - 3} \right) - 3}} = \dfrac{{ - 15}}{9} = \dfrac{{ - 5}}{3}\)
Tại $x = - 1$ thì \(f\left( { - 1} \right) = \dfrac{{15}}{{2.\left( { - 1} \right) - 3}} = \dfrac{{ - 15}}{5} = - 3\)
Tại \(x = 1\) thì \(f\left( 1 \right) = \dfrac{{15}}{{2.1 - 3}} = - 15\)
Nên ta có bảng

Tìm các giá trị của $x$ sao cho vế phải của công thức có nghĩa
Hàm số \(y = f\left( x \right) = \dfrac{{15}}{{2x - 3}}\) có nghĩa khi \(2x - 3 \ne 0 \Rightarrow 2x \ne 3 \Rightarrow x \ne \dfrac{3}{2}.\)
Tìm các giá trị của $x$ sao cho vế phải của công thức có nghĩa
Hàm số \(y = f\left( x \right) = \dfrac{{15}}{{2x - 3}}\) có nghĩa khi \(2x - 3 \ne 0 \Rightarrow 2x \ne 3 \Rightarrow x \ne \dfrac{3}{2}.\)
Tính $f\left( { - \dfrac{1}{4}} \right) - f\left( {\dfrac{1}{4}} \right)$
Ta có \(f\left( { - \dfrac{1}{4}} \right) = \left| {3.\dfrac{{ - 1}}{4} - 1} \right| = \left| {\dfrac{{ - 7}}{4}} \right| = \dfrac{7}{4}\) ; \(f\left( {\dfrac{1}{4}} \right) = \left| {3.\dfrac{1}{4} - 1} \right| = \left| { - \dfrac{1}{4}} \right| = \dfrac{1}{4}\)
Suy ra \(f\left( { - \dfrac{1}{4}} \right) - f\left( {\dfrac{1}{4}} \right) = \dfrac{7}{4} - \dfrac{1}{4} = \dfrac{3}{2}.\)
Cho bảng giá trị sau. Chọn câu đúng.

Từ bảng giá trị ta thấy với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) nên đại lượng \(y\) là hàm số của đại lượng \(x.\)
Tính $f\left( { - \dfrac{1}{4}} \right) - f\left( {\dfrac{1}{4}} \right)$
Ta có \(f\left( { - \dfrac{1}{4}} \right) = \left| {3.\dfrac{{ - 1}}{4} - 1} \right| = \left| {\dfrac{{ - 7}}{4}} \right| = \dfrac{7}{4}\) ; \(f\left( {\dfrac{1}{4}} \right) = \left| {3.\dfrac{1}{4} - 1} \right| = \left| { - \dfrac{1}{4}} \right| = \dfrac{1}{4}\)
Suy ra \(f\left( { - \dfrac{1}{4}} \right) - f\left( {\dfrac{1}{4}} \right) = \dfrac{7}{4} - \dfrac{1}{4} = \dfrac{3}{2}.\)
Cho các công thức \(2y = x + 3;\, - y = \dfrac{x}{2};\,y = {x^2} + 3\). Có bao nhiêu công thức chứng tỏ rằng \(y\) là hàm số của \(x\)?
+ Ta có: \(2y = x + 3 \Rightarrow y = \dfrac{1}{2}x + \dfrac{3}{2}\). Với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) nên \(2y = x + 3\) là một hàm số.
+ Ta có: \( - y = \dfrac{x}{2} \Rightarrow y = - \dfrac{x}{2}\). Với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) nên \( - y = \dfrac{x}{2}\) là một hàm số.
+ Ta có: \(y = {x^2} + 3\) là một hàm số vì với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\).
Bảng giá trị nào sau đây là đúng với hàm số \(y = f\left( x \right) = \dfrac{{ - 7}}{{x - 3}}\)?
Tại \(x = - 6\) ta có: \(f\left( { - 6} \right) = \dfrac{{ - 7}}{{ - 6 - 3}} = \dfrac{7}{9}\).
Tại \(x = - 3\) thì \(f\left( { - 3} \right) = \dfrac{{ - 7}}{{ - 3 - 3}} = \dfrac{7}{6}\).
Tại \(x = - 2\) thì \(f\left( { - 2} \right) = \dfrac{{ - 7}}{{ - 2 - 3}} = \dfrac{7}{5}\).
Tại \(x = 1\) thì \(f\left( 1 \right) = \dfrac{{ - 7}}{{1 - 3}} = \dfrac{7}{2}\).
Nên ta có bảng:

Tìm các giá trị của \(x\) sao cho vế phải của công thức có nghĩa.
Hàm số \(y = f\left( x \right) = \dfrac{{ - 7}}{{x - 3}}\) có nghĩa khi \(x - 3 \ne 0 \Rightarrow x \ne 3\).
Tìm các giá trị của \(x\) sao cho vế phải của công thức có nghĩa.
Hàm số \(y = f\left( x \right) = \dfrac{{ - 7}}{{x - 3}}\) có nghĩa khi \(x - 3 \ne 0 \Rightarrow x \ne 3\).
Một hàm số được cho bằng công thức \(y = f\left( x \right) = \dfrac{{2x - 5}}{3}.\) Tính \(f\left( { - 1} \right);f\left( 2 \right)\).
Ta có: \(f( - 1) = \dfrac{{2.( - 1) - 5}}{3} = - \dfrac{7}{3}\)
\(f\left( 2 \right) = \dfrac{{2.2 - 5}}{3} = - \dfrac{1}{3}\)
Vậy \(f( - 1) = - \dfrac{7}{3};f\left( 2 \right) = - \dfrac{1}{3}.\)
Một hàm số được cho bằng công thức \(y = f(x) = - 2{x^2}.\) Tính \(f\left( { - 6} \right) - f\left( 6 \right)\).
Ta có: \(f\left( { - 6} \right) = - 2.{\left( { - 6} \right)^2} = - 72\) và \(f\left( 6 \right) = - {2.6^2} = - 72\).
Khi đó \(f\left( { - 6} \right) - f\left( 6 \right) = - 72 - ( - 72) = 0\).
Cho hàm số \(y = f(x) = - 5{x^2} - 7\). So sánh \(f\left( x \right)\) và \(f\left( { - x} \right) + 2\).
Ta có: \(f(x) = - 5{x^2} - 7\) và \(f\left( { - x} \right) + 2 = - 5.{( - x)^2} - 7 + 2 = - 5{x^2} - 5\)
Suy ra \(f\left( x \right) - (f\left( { - x} \right) + 2) = - 5{x^2} - 7 - ( - 5{x^2} - 5) = - 2 < 0\)
Vậy \(f\left( x \right) < f\left( { - x} \right) + 2\).
Tìm \(x\), biết \(f\left( x \right) = 5.\)
Từ \(f\left( x \right) = 5\) ta có \(\left| {3 + 4x} \right| = 5\)

Vậy \(x = \dfrac{1}{2}\) hoặc \(x = - 2.\)









