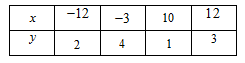
Câu hỏi:
2 năm trước
Cho các công thức \(2y = x + 3;\, - y = \dfrac{x}{2};\,y = {x^2} + 3\). Có bao nhiêu công thức chứng tỏ rằng \(y\) là hàm số của \(x\)?
Trả lời bởi giáo viên
Đáp án đúng: d
+ Ta có: \(2y = x + 3 \Rightarrow y = \dfrac{1}{2}x + \dfrac{3}{2}\). Với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) nên \(2y = x + 3\) là một hàm số.
+ Ta có: \( - y = \dfrac{x}{2} \Rightarrow y = - \dfrac{x}{2}\). Với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) nên \( - y = \dfrac{x}{2}\) là một hàm số.
+ Ta có: \(y = {x^2} + 3\) là một hàm số vì với mỗi giá trị của \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\).