Đồ thị hàm số $y = ax$ $( a ≠ 0)$ là :
Theo định nghĩa đồ thị hàm số $y = ax$ là một đường thẳng đi qua gốc tọa độ.
Điểm thuộc đồ thị hàm số $y = - 2x$ là :
Thay tọa độ các điểm $M,N,P$ vào hàm số đều không thỏa mãn, chỉ có điểm $Q\left( { - 1;2} \right)$ thỏa mãn vì: \(2 = - 2.( - 1)\).
Đồ thị hàm số \(y = - 5x\) không đi qua điểm:
Thay điểm $M\left( {1;5} \right)$ vào hàm số $y = - 5x$ ta thấy \(5 \ne 1.( - 5) = - 5\) nên đồ thị hàm số $y = - 5x$ không đi qua $M\left( {1;5} \right).$
Điểm $B\left( { - 2;6} \right)$ không thuộc đồ thị hàm số
Ta thấy: \(6 \ne {\left( { - 2} \right)^2} = 4\) nên điểm $B\left( { - 2;6} \right)$không thuộc đồ thị hàm số \(y = {x^2}\).
Cho hàm số \(y = 5x.\) Trong các điểm \(A(1;2);\,\,B(2;10);\,\,C( - 2;10);\,\,D\left( {\dfrac{{ - 1}}{5}; - 1} \right)\) có bao nhiêu điểm thuộc đồ thị hàm số \(y = 5x.\)
Đặt \(y = f(x) = 5x\).
Xét $A\left( {1;2} \right)$ có \(x = 1;\,\,\,y = 2\). Khi đó \(f(1) = 5.1 = 5 \ne 2\), tức \(2 \ne f(1)\).
Vậy điểm $A$ không thuộc đồ thị hàm số \(y = 5x.\)
Xét điểm $B\left( {2;10} \right)$ có $x = 2;y = 10$. Khi đó \(f(2) = 5.2 = 10\), tức là \(10 = f(2)\)
Vậy điểm B thuộc đồ thị hàm số \(y = 5x.\)
Tương tự ta có \(f( - 2) = - 10 \ne 10;\,\,f\left( {\dfrac{{ - 1}}{5}} \right) = - 1\) nên $C$ không thuộc đồ thị, điểm $D$ thuộc đồ thị trên.
Vậy có hai điểm thuộc đồ thị hàm số \(y = 5x\) là điểm \(B\left( {2;10} \right)\) và \(D\left( { - \dfrac{1}{5}; - 1} \right).\)
Đồ thị hàm số \(y = - \dfrac{3}{2}x\) là đường thẳng nào trong hình vẽ sau:
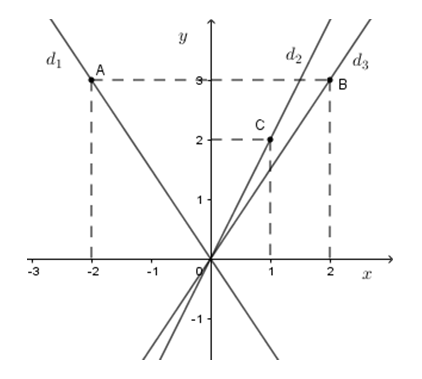
+ Với \(A( - 2;3)\) ta thay \(x = - 2;y = 3\) vào \(y = - \dfrac{3}{2}x\) ta được \(3 = - \dfrac{3}{2}.( - 2)\) hay \(3 = 3\)(luôn đúng). Do đó điểm \(A( - 2;3)\) thuộc đồ thị hàm số \(y = - \dfrac{3}{2}x\).
+ Với \(B(2;3)\) ta thay \(x = 2;y = 3\) vào \(y = - \dfrac{3}{2}x\) ta được \(3 = - \dfrac{3}{2}.2\) hay \(3 = - 3\)(vô lí). Do đó điểm \(B(2;3)\) không thuộc đồ thị hàm số \(y = - \dfrac{3}{2}x\).
+ Với \(C(1;2)\) ta thay \(x = 1;y = 2\) vào \(y = - \dfrac{3}{2}x\) ta được \(2 = - \dfrac{3}{2}.1\) hay \(2 = - \dfrac{3}{2}\)(vô lí). Do đó điểm \(C(1;2)\) không thuộc đồ thị hàm số \(y = - \dfrac{3}{2}x\).
Đồ thị hàm số \(y = - \dfrac{3}{2}x\) là đường thẳng đi qua gốc tọa độ và \(A\left( { - 2;3} \right)\) nên dựa vào hình vẽ ta thấy đường thẳng \({d_1}\) là đồ thị của hàm số \(y = - \dfrac{3}{2}x\).
\(x\) có thể nhận điều kiện nào dưới đây để \(f\left( x \right) \ge 2.\)
Từ đồ thị hàm số \(y = f\left( x \right)\) đã cho, nếu \(x \ge 3\) thì ta có \(f\left( x \right) \ge 2\).
Tìm \(f\left( { - 2} \right);f\left( 3 \right)\).
Từ đồ thị hàm số \(y = f\left( x \right)\)đã cho, ta có \(f\left( { - 2} \right) = 1;f\left( 3 \right) = 2.\)
Tìm \(f\left( { - 2} \right);f\left( 3 \right)\).
Từ đồ thị hàm số \(y = f\left( x \right)\)đã cho, ta có \(f\left( { - 2} \right) = 1;f\left( 3 \right) = 2.\)
Cho đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là đường thẳng OB trên hình vẽ. Khi đó hệ số \(a\) bằng:
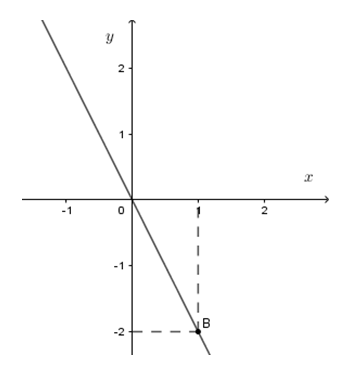
Từ đồ thị hàm số ta thấy điểm \(B\left( {1; - 2} \right)\) thuộc đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) nên ta thay \(x = 1;y = - 2\) vào hàm số \(y = ax\) ta được: \( - 2 = a.1 \Rightarrow a = - 2\,\) (thỏa mãn)
Vậy \(a = - 2.\)
Đồ thị hàm số \(y = ax\,\left( {a \ne 0} \right)\) là …. đi qua gốc tọa độ. Cụm từ thích hợp điền vào chỗ trống là:
Theo định nghĩa, đồ thị hàm số \(y = ax\,\left( {a \ne 0} \right)\) là một đường thẳng đi qua gốc tọa độ.
Điểm thuộc đồ thị hàm số \(y = \dfrac{1}{2}x\) là:
+ Với \(M\left( {1;2} \right)\) ta thay \(x = 1;y = 2\) vào công thức hàm số \(y = \dfrac{1}{2}x\) ta được \(2 = \dfrac{1}{2}.1\) hay \(2 = \dfrac{1}{2}\) (vô lí). Vậy điểm \(M\left( {1;2} \right)\) không thuộc đồ thị hàm số \(y = \dfrac{1}{2}x\).
+ Với \(N\left( {1;4} \right)\) ta thay \(x = 1;y = 4\) vào công thức hàm số \(y = \dfrac{1}{2}x\) ta được \(4 = \dfrac{1}{2}.1\) hay \(4 = \dfrac{1}{2}\) (vô lí). Vậy điểm \(N\left( {1;4} \right)\) không thuộc đồ thị hàm số \(y = \dfrac{1}{2}x\).
+ Với \(P\left( { - 1; - 2} \right)\) ta thay \(x = - 1;y = - 2\) vào công thức hàm số \(y = \dfrac{1}{2}x\) ta được \( - 2 = \dfrac{1}{2}.( - 1)\) hay \( - 2 = - \dfrac{1}{2}\) (vô lí). Vậy điểm \(P\left( { - 1; - 2} \right)\) không thuộc đồ thị hàm số \(y = \dfrac{1}{2}x\).
+ Với \(Q\left( {2;1} \right)\) ta thay \(x = 2;y = 1\) vào công thức hàm số \(y = \dfrac{1}{2}x\) ta được \(1 = \dfrac{1}{2}.2\) hay \(1 = 1\) (luôn đúng). Vậy điểm \(Q\left( {2;1} \right)\) thuộc đồ thị hàm số \(y = \dfrac{1}{2}x\).
Đồ thị hàm số \(y = \dfrac{6}{5}x\) không đi qua điểm nào dưới đây?
+ Với \(M\left( {1;\dfrac{6}{5}} \right)\) ta thay \(x = 1; y = \dfrac{6}{5}\) vào công thức hàm số \(y = \dfrac{6}{5}x\) ta được \(\dfrac{6}{5} = \dfrac{6}{5}.1\) hay \(\dfrac{6}{5} = \dfrac{6}{5}\) (luôn đúng). Vậy đồ thị hàm số \(y = \dfrac{6}{5}x\) đi qua điểm \(M\left( {1;\dfrac{6}{5}} \right)\).
+ Với \(N\left( {5;6} \right)\) ta thay \(x = 5;y = 6\) vào công thức hàm số \(y = \dfrac{6}{5}x\) ta được \(6 = \dfrac{6}{5}.5\) hay \(6 = 6\) (luôn đúng). Vậy đồ thị hàm số \(y = \dfrac{6}{5}x\) đi qua điểm \(N\left( {5;6} \right)\).
+ Với \(P\left( { - 1;6} \right)\) ta thay \(x = - 1;y = 6\) vào công thức hàm số \(y = \dfrac{6}{5}x\) ta được \(6 = \dfrac{6}{5}.( - 1)\) hay \(6 = - \dfrac{6}{5}\) (vô lí). Vậy đồ thị hàm số \(y = \dfrac{6}{5}x\) không đi qua điểm \(P\left( { - 1;6} \right)\).
+ Với \(Q\left( { - 10; - 12} \right)\) ta thay \(x = - 10;y = - 12\) vào công thức hàm số \(y = \dfrac{6}{5}x\) ta được \( - 12 = \dfrac{6}{5}.( - 10)\) hay \( - 12 = - 12\) (luôn đúng). Vậy đồ thị hàm số \(y = \dfrac{6}{5}x\) đi qua điểm \(Q\left( { - 10; - 12} \right)\).
Điểm \(M\left( { - 1;3} \right)\) không thuộc đồ thị hàm số:
+ Thay \(x = - 1;y = 3\) vào công thức hàm số \(y = - 3x\) ta được \(3 = - 3.( - 1)\) hay \(3 = 3\) (luôn đúng). Vậy điểm \(M\left( { - 1;3} \right)\) thuộc đồ thị hàm số \(y = - 3x\).
+ Thay \(x = - 1;y = 3\) vào công thức hàm số \(y = x + 4\) ta được \(3 = - 1 + 4\) hay \(3 = 3\) (luôn đúng). Vậy điểm \(M\left( { - 1;3} \right)\) thuộc đồ thị hàm số \(y = x + 4\).
+ Thay \(x = - 1;y = 3\) vào công thức hàm số \(y = 2 - x\) ta được \(3 = 2 - ( - 1)\) hay \(3 = 3\) (luôn đúng). Vậy điểm \(M\left( { - 1;3} \right)\) thuộc đồ thị hàm số \(y = 2 - x\).
+ Thay \(x = - 1;y = 3\) vào công thức hàm số \(y = 2x + 3\) ta được \(3 = 2.( - 1) + 3\) hay \(3 = 1\) (vô lí). Vậy điểm \(M\left( { - 1;3} \right)\) không thuộc đồ thị hàm số \(y = 2x + 3\).
Cho hình vẽ sau:
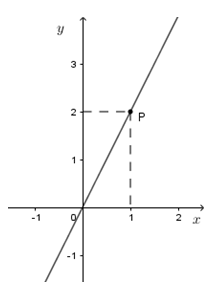
Đường thẳng \(OP\) là đồ thị hàm số nào dưới đây?
Nhận thấy đường thẳng \(OP\) là đường thẳng đi qua gốc tọa độ nên đường thẳng \(OP\) là đồ thị của hàm số \(y = ax\,\,(a \ne 0)\). Theo hình vẽ ta có điểm \(P(1;2)\) thuộc vào đồ thị hàm số \(y = ax\).
Khi đó thay \(x = 1;y = 2\) vào \(y = ax\) ta được: \(2 = a.1 \Rightarrow a = 2\) (thỏa mãn)
Vậy đường thẳng \(OP\) là đồ thị hàm số \(y = 2x.\)
Đồ thị của hàm số \(y = - 2,5x\) là đường thẳng \(OB\) với \(O\left( {0;0} \right)\) và điểm
+ Thay \(x = - 2;y = - 5\) vào công thức hàm số \(y = - 2,5x\) ta được \( - 5 = - 2,5.( - 2)\) hay \( - 5 = 5\) (vô lí). Vậy điểm \(B\,( - 2; - 5)\) không thuộc đồ thị hàm số \(y = - 2,5x\).
+ Thay \(x = 5;y = - 2\) vào công thức hàm số \(y = - 2,5x\) ta được \( - 2 = - 2,5.5\) hay \( - 2 = - \dfrac{{25}}{2}\) (vô lí). Vậy điểm \(B\,(5; - 2)\) không thuộc đồ thị hàm số \(y = - 2,5x\).
+ Thay \(x = 2;y = - 5\) vào công thức hàm số \(y = - 2,5x\) ta được \( - 5 = - 2,5.2\) hay \( - 5 = - 5\) (luôn đúng). Vậy điểm \(B\,(2; - 5)\)thuộc đồ thị hàm số \(y = - 2,5x\).
+ Thay \(x = 4;y = 10\) vào công thức hàm số \(y = - 2,5x\) ta được \(10 = - 2,5.4\) hay \(10 = - 10\) (vô lí). Vậy điểm \(B\,(4;10)\) không thuộc đồ thị hàm số \(y = - 2,5x\).
Cho hàm số \(y = - 8x.\) Trong các điểm \(A\,( - 1;8);\,\,B\,(2; - 4);\,\,C\,( - \dfrac{1}{2};4);\,\,D\left( {\dfrac{{ - 1}}{8}; - 1} \right)\) có bao nhiêu điểm thuộc đồ thị hàm số \(y = - 8x.\)
+ Với \(A( - 1;8)\) ta thay \(x = - 1;y = 8\) vào hàm số \(y = - 8x\) ta được \(8 = - 8.( - 1)\) hay \(8 = 8\) (luôn đúng). Vậy điểm \(A( - 1;8)\) thuộc đồ thị hàm số \(y = - 8x\).
+ Với \(\,B(2; - 4)\) ta thay \(x = 2;y = - 4\) vào hàm số \(y = - 8x\) ta được \( - 4 = - 8.2\) hay \( - 4 = - 16\) (vô lí). Vậy điểm \(\,B(2; - 4)\) không thuộc đồ thị hàm số \(y = - 8x\).
+ Với \(C( - \dfrac{1}{2};4)\) ta thay \(x = - \dfrac{1}{2};y = 4\) vào hàm số \(y = - 8x\) ta được \(4 = - 8.\left( { - \dfrac{1}{2}} \right)\) hay \(4 = 4\) (luôn đúng). Vậy điểm \(C( - \dfrac{1}{2};4)\) thuộc đồ thị hàm số \(y = - 8x\).
+ Với \(\,\,D\left( {\dfrac{{ - 1}}{8}; - 1} \right)\) ta thay \(x = \dfrac{{ - 1}}{8};y = - 1\) vào hàm số \(y = - 8x\) ta được \( - 1 = - 8.\left( {\dfrac{{ - 1}}{8}} \right)\) hay \( - 1 = 1\) (vô lí). Vậy điểm \(\,\,D\left( {\dfrac{{ - 1}}{8}; - 1} \right)\) không thuộc đồ thị hàm số \(y = - 8x\).
Vậy có hai điểm thuộc đồ thị hàm số \(y = - 8x\) là điểm \(A( - 1;8)\) và \(C( - \dfrac{1}{2};4)\).
Cho hàm số \(y = \dfrac{{m - 2}}{3}x\). Xác định \(m\) biết đồ thị hàm số đi qua điểm \(A\left( { - 3;5} \right).\)
Thay \(x = - 3;y = 5\) vào \(y = \dfrac{{m - 2}}{3}x\) ta được \(5 = \dfrac{{m - 2}}{3}.( - 3) \Rightarrow 5 = 2 - m \Rightarrow m = - 3\)
Vậy \(m = - 3.\)
Cho ba điểm \(M(2;6); N( - 3; - 9); P(2,5;7,5)\). Chọn câu đúng.
Xét \(M(2;6)\) ta có: \(6 = 3.2\) nên điểm \(M(2;6)\) thuộc đồ thị hàm số \(y = 3x\).
Xét \(N( - 3; - 9)\) ta có: \( - 9 = 3.( - 3)\) nên điểm \(N( - 3; - 9)\) thuộc đồ thị hàm số \(y = 3x\).
Xét \(P(2,5;7,5)\) ta có: \(7,5 = 3.2,5\) nên điểm \(P(2,5;7,5)\) thuộc đồ thị hàm số \(y = 3x\).
Ta thấy ba điểm \(M,N,P\) cùng thuộc đồ thị hàm số \(y = 3x\) nên ba điểm \(M,N,P\) thẳng hàng.
Đồ thị hàm số \(y = 2,5x\) nằm ở những góc phần tư nào của hệ trục tọa độ?
Đồ thị hàm số \(y = 2,5x\) có \(a = 2,5 > 0\) nên đồ thị hàm số \(y = 2,5x\) nằm ở góc phần tư thứ nhất và thứ ba.

