Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là đường thẳng OD với điểm \(D\left( {1,2; - 6} \right).\) Hãy xác định công thức của hàm số trên.
Đồ thị của hàm số \(y = ax\left( {a \ne 0} \right)\) là đường thẳng OD đi qua điểm \(D\left( {1,2; - 6} \right)\), do đó ta thay \(x = 1,2;y = - 6\) vào hàm số \(y = ax\) ta được \( - 6 = a.1,2 \Rightarrow a = - 5\) (thỏa mãn).
Công thức của hàm số đã cho là: \(y = - 5x\).
Đồ thị của hàm số \(y = ax\left( {a \ne 0} \right)\) đi qua điểm \(A(5; - 2)\). Tính hệ số a?
Đồ thị của hàm số \(y = ax\left( {a \ne 0} \right)\) đi qua điểm \(A(5; - 2)\), do đó ta thay \(x = 5;y = - 2\) vào hàm số \(y = ax\) ta được \( - 2 = a.5 \Rightarrow a = - \dfrac{2}{5}\) (thỏa mãn).
Cho đồ thị hàm số \(y = - 7x - 2\) và điểm C thuộc đồ thị đó. Tìm tọa độ điểm C nếu biết tung độ điểm C là \(12\)?
Thay \(y = 12\) vào \(y = - 7x - 2\) ta được \(12 = - 7x - 2 \Rightarrow - 7x = 14 \Rightarrow x = - 2\)
Suy ra tọa độ điểm C là \(C\left( { - 2;{\rm{ }}12} \right)\;\).
Cho đồ thị hàm số \(y = - 12x\) và điểm A thuộc đồ thị đó. Tìm tọa độ điểm A nếu biết hoành độ điểm A là \( - \dfrac{1}{2}\)?
Thay \(x = - \dfrac{1}{2}\) vào \(y = - 12x\) ta được \(y = - 12.\left( { - \dfrac{1}{2}} \right) = 6\)
Suy ra tọa độ điểm A là \(A\left( { - \dfrac{1}{2};6} \right)\;\).
Tìm \(f\left( { - 2} \right);f\left( 1 \right)\)
Từ đồ thị hàm số ta có \(f\left( { - 2} \right) = 1;f\left( 1 \right) = 2.\)
Tìm \(f\left( { - 2} \right);f\left( 1 \right)\)
Từ đồ thị hàm số ta có \(f\left( { - 2} \right) = 1;f\left( 1 \right) = 2.\)
Tìm \(f\left( { - 2} \right);f\left( 1 \right)\)
Từ đồ thị hàm số ta có \(f\left( { - 2} \right) = 1;f\left( 1 \right) = 2.\)
Đồ thị hàm số \(y = - 4x\) nằm ở những góc phần tư nào của hệ trục tọa độ?
Ta có đồ thị hàm số \(y = - 4x\) là đường thẳng đi qua hai điểm \(O\left( {0;0} \right);A\left( { - 1;4} \right)\) như hình vẽ.
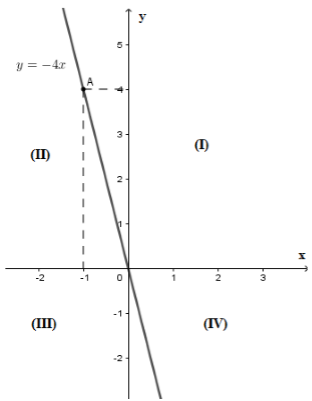
Nên đồ thị hàm số \(y = - 4x\) thuộc góc phần tư thứ hai và thứ tư.
Cho đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là đường thẳng OM trên hình vẽ. Khi đó hệ số \(a\) bằng
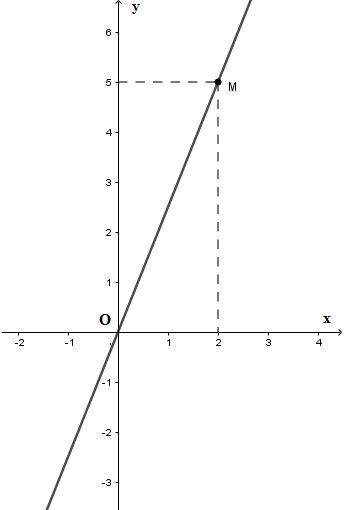
Từ đồ thị hàm số ta thấy điểm \(M\left( {2;5} \right)\) thuộc đồ thị hàm số nên ta thay \(x = 2;y = 5\) vào hàm số \(y = ax\left( {a \ne 0} \right)\), được: \(5 = a.2 \Rightarrow a = \dfrac{5}{2}\,\left( {TM} \right)\)
Vậy \(a = \dfrac{5}{2}.\)
Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số \(y = ax\left( {a \ne 0} \right)\) là đường thẳng OA với điểm $A( - 1; - 3).$ Hãy xác định công thức của hàm số trên.
Đồ thị của hàm số \(y = ax\left( {a \ne 0} \right)\) là đường thẳng OA đi qua điểm $A( - 1; - 3)$, do đó khi \(x = - 1\) thì \(y = - 3\)
Nên ta có \( - 3 = a.\left( { - 1} \right) \Rightarrow a = 3\) (TM)
Công thức của hàm số đã cho là: \(y = 3x\) .
Tìm \(x\) sao cho \(f\left( x \right) \ge 0.\)
Từ đồ thị hàm số ta có \(f\left( x \right) \ge 0\) với mọi $x.$
Cho hình vẽ sau:
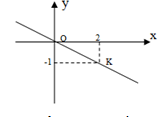
Đường thẳng \(OK\) là đồ thị hàm số nào dưới đây?
Ta gọi hàm số cần tìm là \(y = ax\) $( a \ne 0)$. Khi đó thay \(x = 2;y = -1\) vào \(y = ax\) ta được: \( - 1 = a.2 \Rightarrow a = \dfrac{{ - 1}}{2}\)
Nên \(y = - 0,5x.\)
Đồ thị của hàm số $y = \dfrac{1}{5}x$ là đường thẳng $OA$ với $O\left( {0;0} \right)$ và
Ta thấy $A\left( {5;1} \right)$ thỏa mãn hàm số \(y = \dfrac{1}{5}x\) vì $1=\dfrac{1}{5}.5$ \( \Leftrightarrow 1 = 1\) (luôn đúng).
Nên đồ thị hàm số \(y = \dfrac{1}{5}x\) đi qua điểm $A\left( {5;1} \right).$
Đồ thị hàm số \(y = 3x\) là đường thẳng nào trong hình vẽ sau:
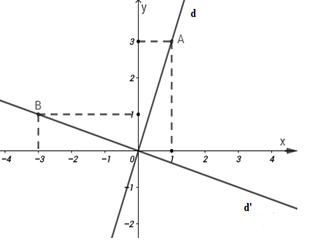
Đồ thị hàm số \(y = 3x\) là đường thẳng đi qua gốc tọa độ và \(A\left( {1;3} \right)\) nên trên hình vẽ đường thẳng \(d\) là đồ thị của hàm số \(y = 3x.\)
Cho hàm số \(y = \left( {2m + 1} \right)x\). Xác định \(m\) biết đồ thị hàm số đi qua điểm \(A\left( { - 1;1} \right).\)
Thay tọa độ \(A:x = - 1;y = 1\) vào \(y = \left( {2m + 1} \right)x\) ta được \(1 = \left( {2m + 1} \right).\left( { - 1} \right) \Rightarrow 2m + 1 = - 1\)
\( \Rightarrow 2m = - 2 \Rightarrow m = - 1\)
Vậy \(m = - 1.\)
Cho ba điểm \(A( - 1;4);B(2; - 8);C(1,5; - 6)\). Chọn câu đúng.
Xét \(A\left( { - 1;\,\,4} \right)\) ta có: \(4 = - 4.\left( { - 1} \right)\) nên điểm A thuộc đồ thị hàm số \(y = - 4x.\)
Xét \(B\left( {2; - 8} \right)\) ta có: \( - 8 = - 4.2\) nên điểm B thuộc đồ thị hàm số \(y = - 4x.\)
Xét \(C\left( {1,5;\,\, - 6} \right)\) ta có: \( - 6 = - 4.1,5\) nên điểm C thuộc đồ thị hàm số \(y = - 4x.\)
Ta thấy ba điểm $A,B,C$ cùng thuộc đồ thị hàm số \(y = - 4x\), nên ba điểm $A,B,C$ thẳng hàng.
Đồ thị của hàm số \(y = ax\left( {a \ne 0} \right)\) đi qua điểm \(A\left( {3; - \dfrac{1}{9}} \right)\) . Tính hệ số a?
Đồ thị của hàm số \(y = ax\left( {a \ne 0} \right)\) là đường thẳng OA đi qua điểm $A\left( {3; - \dfrac{1}{9}} \right)$, do đó khi \(x = 3\) thì \(y = - \dfrac{1}{9}\)
Nên ta có \( - \dfrac{1}{9} = a.3 \Rightarrow a = \left( { - \dfrac{1}{9}} \right):3 = \dfrac{{ - 1}}{{27}}\) (TM)
Vậy $a=\dfrac{{ - 1}}{{27}}$.
Cho đồ thị hàm số \(y = - 3x + 1\) và điểm C thuộc đồ thị đó. Tìm tọa độ điểm C nếu biết tung độ điểm C là 1?
Thay \(y = 1\) vào \(y = - 3x + 1\) ta được \(1 = - 3x + 1 \Leftrightarrow - 3x = 0 \Leftrightarrow x = 0\)
Suy ra tọa độ điểm C là $C\left( {0;{\rm{ }}1} \right)\;$.
Cho đồ thị hàm số $y = 6x\;$ và điểm A thuộc đồ thị đó. Tìm tọa độ điểm A nếu biết hoành độ điểm A là 2?
Thay \(x = 2\) vào \(y = 6x\) ta được \(y = 6.2 = 12\)
Suy ra tọa độ điểm A là $A\left( {2;{\rm{ }}12} \right)\;$.
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau:
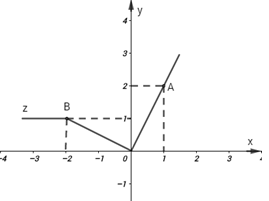
Tìm \(f\left( { - 2} \right);f\left( 1 \right)\)
Từ đồ thị hàm số ta có \(f\left( { - 2} \right) = 1;f\left( 1 \right) = 2.\)

