Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ sau:
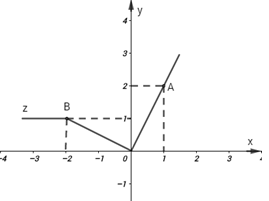
Tìm \(x\) sao cho \(f\left( x \right) \ge 0.\)
Từ đồ thị hàm số ta có \(f\left( x \right) \ge 0\) với mọi $x.$
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{x - 1}}{2}\,\,khi\,x \ge 2\\ - x - 7\,\,khi\,\,x < 2\end{array} \right.\)
Tính \(f\left( 3 \right);f\left( 0 \right);f\left( 2 \right);f\left( { - 2} \right)\).
Ta có hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{x - 1}}{2}\,\,khi\,x \ge 2\\ - x - 7\,\,khi\,\,x < 2\end{array} \right.\)
Với \(x = 3\) thì \(f\left( x \right) = \dfrac{{x - 1}}{2}\). Do đó ta thay \(x = 3\) vào \(f\left( x \right) = \dfrac{{x - 1}}{2}\) ta được \(f\left( 3 \right) = \dfrac{{3 - 1}}{2} = 1\);
Với \(x = 0\) thì \(f\left( x \right) = - x - 7\). Do đó ta thay \(x = 0\) vào \(f\left( x \right) = - x - 7\) ta được \(f\left( 0 \right) = - 0 - 7 = - 7\);
Với \(x = 2\) thì \(f\left( x \right) = \dfrac{{x - 1}}{2}\). Do đó ta thay \(x = 2\) vào \(f\left( x \right) = \dfrac{{x - 1}}{2}\) ta được \(f\left( 2 \right) = \dfrac{{2 - 1}}{2} = \dfrac{1}{2}\);
Với \(x = - 2\) thì \(f\left( x \right) = - x - 7\). Do đó ta thay \(x = - 2\) vào \(f\left( x \right) = - x - 7\) ta được \(f\left( { - 2} \right) = - ( - 2) - 7 = - 5\).
Vậy \(f\left( 3 \right) = 1;f\left( 0 \right) = - 7;f\left( 2 \right) = \dfrac{1}{2};f\left( { - 2} \right) = - 5\).

