So sánh hai góc \(\widehat {CAD}\) và \(\widehat {CBD}.\)
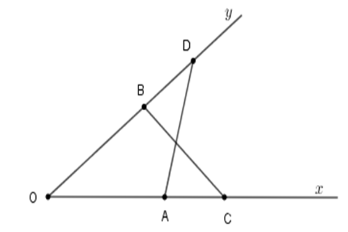
Vì \(\Delta OAD = \Delta OBC\,\left( {c - g - c} \right).\) Suy ra \(\widehat {OBC} = \widehat {OAD}\) (hai góc tương ứng bằng nhau)
Lại có \(\widehat {OBC} + \widehat {CBD} = 180^\circ ;\,\widehat {OAD} + \widehat {DAC} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {CBD} = 180^\circ - \widehat {OBC}\) và \(\widehat {CAD} = 180^\circ - \widehat {OAD}\) mà \(\widehat {OBC} = \widehat {OAD}\) (cmt)
Suy ra \(\widehat {CBD} = \widehat {CAD}.\)
Chọn câu đúng.
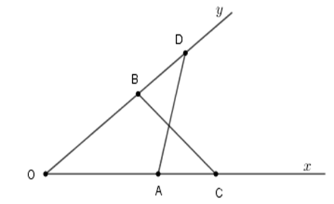
Xét tam giác \(OAD\) và tam giác \(OBC\) có
$OA = OB,$ góc \(O\) chung, $OD = OC$ suy ra \(\Delta OAD = \Delta OBC\,\left( {c - g - c} \right).\)
Chọn câu đúng.

Xét tam giác \(OAD\) và tam giác \(OBC\) có
$OA = OB,$ góc \(O\) chung, $OD = OC$ suy ra \(\Delta OAD = \Delta OBC\,\left( {c - g - c} \right).\)
Tính \(\widehat {BOC}.\)
Từ câu trước ta có \(\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)\)\( \Rightarrow \widehat {BCA} = \widehat {BAC}\) (hai góc tương ứng) (1)
Tương tự ta có \(\Delta BCE = \Delta ACE\left( {c - g - c} \right)\) \( \Rightarrow \widehat {CBA} = \widehat {BAC}\) (hai góc tương ứng) (2)
Từ (1) và (2) ta có \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB}\). Mà \(\widehat {ABC} + \widehat {BAC} + \widehat {ACB} = 180^\circ \) (định lý tổng ba góc của tam giác) nên \(\widehat {ABC} = \widehat {BAC} = \widehat {ACB} = \dfrac{{180^\circ }}{3} = 60^\circ .\)
Lại có \(\widehat {ABD} = \widehat {CBD}\) (cmt) nên \(\widehat {CBO} = \dfrac{{\widehat {ABC}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ \); \(\widehat {ACE} = \widehat {BCE} = \dfrac{{\widehat {ACB}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ .\)
Xét tam giác \(BOC\) có \(\widehat {BOC} + \widehat {OBC} + \widehat {OCB} = 180^\circ \) (định lý tổng ba góc của một tam giác)
Nên \(\widehat {BOC} = 180^\circ - 30^\circ - 30^\circ = 120^\circ .\)
Vậy \(\widehat {BOC} = 120^\circ .\)
Chọn câu đúng.
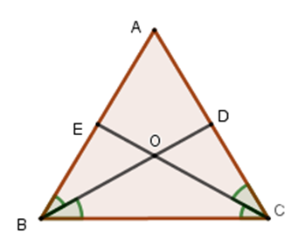
Vì \(BD\) và \(CE\) là tia phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) nên \(\widehat {ABD} = \widehat {CBD}\) và \(\widehat {ACE} = \widehat {BCE}.\)
Xét tam giác \(ABD\) và tam giác \(CBD\) có:
+ \(AB = AC\,\left( {gt} \right)\)
+ \(\widehat {ABD} = \widehat {CBD}\) (cmt)
+ Cạnh \(BD\) chung
Suy ra \(\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {ADB} = \widehat {BDC}\) (hai góc tương ứng); \(DC = AD\) (hai cạnh tương ứng) nên C sai.
Mà \(\widehat {ADB} + \widehat {CDB} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {ADB} = \widehat {CDB} = \dfrac{{180^\circ }}{2} = 90^\circ \) . Do đó \(BD \bot AC.\)
Tương tự ta có \(CE \bot AB.\)
Chọn câu đúng.

Vì \(BD\) và \(CE\) là tia phân giác của góc \(\widehat {ABC}\) và \(\widehat {ACB}\) nên \(\widehat {ABD} = \widehat {CBD}\) và \(\widehat {ACE} = \widehat {BCE}.\)
Xét tam giác \(ABD\) và tam giác \(CBD\) có:
+ \(AB = AC\,\left( {gt} \right)\)
+ \(\widehat {ABD} = \widehat {CBD}\) (cmt)
+ Cạnh \(BD\) chung
Suy ra \(\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)\)
\( \Rightarrow \widehat {ADB} = \widehat {BDC}\) (hai góc tương ứng); \(DC = AD\) (hai cạnh tương ứng) nên C sai.
Mà \(\widehat {ADB} + \widehat {CDB} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {ADB} = \widehat {CDB} = \dfrac{{180^\circ }}{2} = 90^\circ \) . Do đó \(BD \bot AC.\)
Tương tự ta có \(CE \bot AB.\)
Gọi \(I\) là giao của \(AB\) và \(Oz.\) Tính góc \(AIC.\)
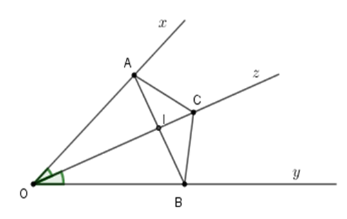
Xét tam giác \(AOI\) và \(BOI\) có
+ \(OA = OB\left( {gt} \right)\)
+ \(\widehat {AOI} = \widehat {BOI}\) (tính chất tia phân giác)
+ Cạnh $OI$ chung
Suy ra \(\Delta AOI = \Delta BOI\left( {c - g - c} \right)\)
Do đó \(\widehat {AIO} = \widehat {BIO}\) (hai góc tương ứng) mà \(\widehat {AIO} + \widehat {BIO} = 180^\circ \) nên \(\widehat {AIO} = \widehat {BIO} = \dfrac{{180^\circ }}{2} = 90^\circ \)
Hay \(OC \bot AB \Rightarrow \widehat {AIC} = 90^\circ .\)
Chọn câu sai.
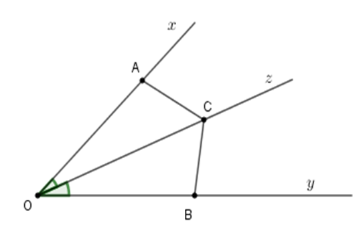
Xét tam giác \(AOC\) và \(BOC\) có
+ \(OA = OB\left( {gt} \right)\)
+ \(\widehat {AOC} = \widehat {BOC}\) (tính chất tia phân giác)
+ Cạnh $OC$ chung
Suy ra \(\Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow AC = BC\) (hai cạnh tương ứng); \(\widehat {OAC} = \widehat {OBC}\); \(\widehat {OCA} = \widehat {OCB}\) (hai góc tương ứng)
Từ đó \(CO\) là tia phân giác của \(\widehat {BCA}.\)
Nên B, C, D đúng, A sai.
Chọn câu sai.

Xét tam giác \(AOC\) và \(BOC\) có
+ \(OA = OB\left( {gt} \right)\)
+ \(\widehat {AOC} = \widehat {BOC}\) (tính chất tia phân giác)
+ Cạnh $OC$ chung
Suy ra \(\Delta AOC = \Delta BOC\left( {c - g - c} \right)\)
\( \Rightarrow AC = BC\) (hai cạnh tương ứng); \(\widehat {OAC} = \widehat {OBC}\); \(\widehat {OCA} = \widehat {OCB}\) (hai góc tương ứng)
Từ đó \(CO\) là tia phân giác của \(\widehat {BCA}.\)
Nên B, C, D đúng, A sai.
Cho tam giác \(ABC\) và tam giác \(DEF\) có: \(AB = DE\), \(AC = DF\). Cần thêm một điều kiện gì để hai tam giác \(ABC\) và \(DEF\) bằng nhau theo trường hợp cạnh – góc – cạnh:
Tam giác \(ABC\) và tam giác \(DEF\) có: \(AB = DE\), \(AC = DF\).
Để tam giác \(ABC\) và tam giác \(DEF\) bằng nhau theo trường hợp cạnh – góc – cạnh cần thêm điều kiện về góc xen giữa đó là: \(\widehat A = \widehat D.\)
Cho tam giác \(MNP\) và tam giác \(IJK\) có \(MN = IJ,\) \(\widehat M = \widehat I\), \(MP = IK.\) Phát biểu nào trong trong các phát biểu sau đây là đúng:
Xét \(\Delta MNP\) và \(\Delta IJK\) có:
\(MN = IJ\)
\(MP = IK\)
\(\widehat M = \widehat I\)
\(\Delta MNP = \Delta IJK\) (c.g.c)
Cho hai đoạn thẳng \(BD\) và \(EC\) cắt nhau tại \(A\) sao cho \(AB = AC,AD = AE,AB > AD.\) Phát biểu nào trong các phát biểu sau đây là sai:

Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(AB = AC\,\,(gt)\)
\(\widehat {BAE} = \widehat {CAD}\) (hai góc đối đỉnh)
\(AE = AD(gt)\)
\( \Rightarrow \Delta ABE = \Delta ACD\,(c.g.c)\) (A đúng).
\( \Rightarrow BE = CD\) (hai cạnh tương ứng) (B đúng)
\( \Rightarrow \widehat {ABE} = \widehat {ACD}\) (hai góc tương ứng) (D đúng).
So sánh \(AC\) và \(BD.\)

Xét \(\Delta AOC\) và \(\Delta BOD\) có:
\(OA = OB\) (vì \(O\) là trung điểm \(AB\))
\(OC = OD\) (vì \(O\) là trung điểm \(CD\))
\(\widehat {AOC} = \widehat {BOD}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta AOC = \Delta BOD\,(c.g.c)\)
\( \Rightarrow AC = BD\) (hai cạnh tương ứng bằng nhau).
Chọn câu đúng.

Xét \(\Delta AOC\) và \(\Delta BOD\) có:
\(OA = OB\) (vì \(O\) là trung điểm \(AB\))
\(OC = OD\) (vì \(O\) là trung điểm \(CD\))
\(\widehat {AOC} = \widehat {BOD}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta AOC = \Delta BOD\,(c.g.c)\)
Chọn câu đúng.

Xét \(\Delta AOC\) và \(\Delta BOD\) có:
\(OA = OB\) (vì \(O\) là trung điểm \(AB\))
\(OC = OD\) (vì \(O\) là trung điểm \(CD\))
\(\widehat {AOC} = \widehat {BOD}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta AOC = \Delta BOD\,(c.g.c)\)
Cho tam giác \(DEF\) và tam giác \(MNP\) có \(DE = MN\), \(\widehat E = \widehat N\), \(EF = NP.\)
Biết \(\widehat D = {100^0}\). Số đo góc \(M\) là:
Xét \(\Delta DEF\) và \(\Delta MNP\) có:
\(DE = MN\)
\(\widehat E = \widehat N\)
\(EF = NP\)
\( \Rightarrow \Delta DEF = \Delta MNP\) (c.g.c).
\( \Rightarrow \widehat M = \widehat D = {100^0}\) (hai góc tương ứng).
Cho tam giác \(ABC\) có \(\widehat A = {90^0};\,\widehat B = {50^0}\), tia phân giác \(BD\) của góc \(B\) (\(D \in AC\)). Trên cạnh \(BC\) lấy điểm \(E\) sao cho \(BE = BA.\) Tính số đo góc \(EDC.\)

Xét \(\Delta BDA\) và \(\Delta BDE\) có:
\(BA = BE\left( {gt} \right)\)
\(\widehat {{B_1}} = \widehat {{B_2}}\) (do \(BD\) là tia phân giác của \(\widehat B\))
\(BD\) cạnh chung
\( \Rightarrow \Delta BDA = \Delta BDE\) (c.g.c)
\( \Rightarrow \widehat {ADB} = \widehat {EDB}\) (hai góc tương ứng bằng nhau)
\(BD\) là phân giác của \(\widehat B\) nên \(\widehat {{B_1}} = \widehat {{B_2}}\, = \dfrac{{\widehat B}}{2} = \dfrac{{{{50}^o}}}{2} = {25^o}\)
\(\Delta ABD\) vuông tại \(A\) nên ta có \(\widehat {{B_1}} + \widehat {ADB} = {90^o}\)
\( \Rightarrow \widehat {ADB} = {90^o} - \widehat {{B_1}} = {90^o} - {25^o} = {65^o}.\)
Do đó \(\widehat {ADB} = \widehat {EDB} = {65^o}\)
Ta có \(\widehat {ADB} + \widehat {EDB} + \widehat {EDC} = {180^o}\) (kề bù)
\( \Rightarrow \widehat {EDC} = {180^o} - \left( {\widehat {ADB} + \widehat {EDB}} \right) = {180^o} - \left( {{{65}^o} + {{65}^o}} \right) = {50^o}\).
Cho tam giác \(ABC\) có \(AC > AB,\) tia phân giác của góc \(A\) cắt \(BC\) ở \(D.\) Trên cạnh \(AC\) lấy \(E\) sao cho \(AE = AB.\) Chọn đáp án đúng.

Gọi \(I\) là giao điểm của \(AD\) và \(BE\).
Xét \(\Delta AIB\) và \(\Delta AIE\) có:
\(AI\) cạnh chung
\(\widehat {{A_1}} = \widehat {{A_2}}\) (vì \(AD\) là phân giác \(\widehat A\))
\(AB = AE\) (gt)
\( \Rightarrow \Delta AIB = \Delta AIE\,(c.g.c)\)
\( \Rightarrow \widehat {AIB} = \widehat {AIE}\) (hai góc tương ứng)
\( \Rightarrow IB = IE\) (hai cạnh tương ứng) (1)
Mặt khác \(\widehat {AIB} + \widehat {AIE} = {180^o}\) (hai góc kề bù)
\( \Rightarrow \widehat {AIB} = \widehat {AIE} = 1{80^o}:2 = {90^o}\)
Do đó \(AD \bot \,BE\) (2)
Từ (1) và (2) suy ra \(AD\) là đường trung trực của \(BE.\)
Cho tam giác \(ABC,\) kẻ \(BD\) vuông góc với \(AC,\) kẻ \(CE\) vuông góc với \(AB.\) Trên tia đối của tia \(BD\) lấy điểm \(H\) sao cho \(BH = AC.\) Trên tia đối của tia \(CE,\) lấy điểm \(K\) sao cho \(CK = AB.\) So sánh \(AH,AK.\)
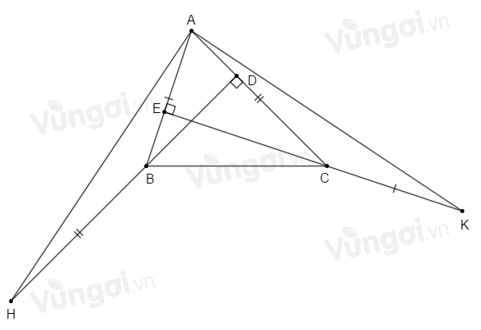
Ta có \(\widehat {ABH}\) là góc ngoài đỉnh \(B\) của \(\Delta ABD\) nên \(\widehat {ABH} = \widehat {BAD} + \widehat {ADB} = \widehat {BAD} + {90^o}\) (1)
\(\widehat {KCA}\) là góc ngoài đỉnh \(C\) của \(\Delta ACE\) nên \(\widehat {KCA} = \widehat {EAC} + \widehat {AEC} = \widehat {EAC} + {90^o}\) (2)
Từ (1) và (2) suy ra \(\widehat {ABH} = \widehat {KCA}\).
Xét \(\Delta ABH\) và \(\Delta KCA\) có:
\(AB = KC\,(gt)\)
\(BH = CA\,(gt)\)
\(\widehat {ABH} = \widehat {KCA}\) (chứng minh trên)
\( \Rightarrow \Delta ABH = \Delta KCA\,(c.g.c)\)
\( \Rightarrow AH = AK\) (hai cạnh tương ứng bằng nhau).
Cho hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại \(O\) là trung điểm của mỗi đoạn thẳng đó. Lấy \(E;\,F\) lần lượt là điểm thuộc đoạn \(AD\) và \(BC\) sao cho \(AE = BF.\) Cho \(OE = 5cm\), tính \(EF.\)

* Xét \(\Delta OAD\) và \(\Delta OBC\) có:
+ \(OA = OB\,\left( {gt} \right)\)
+ \(\widehat {AOD} = \widehat {BOC}\) (đối đỉnh)
+ \(OD = OC\left( {gt} \right)\)
\( \Rightarrow \Delta OAD = \Delta OBC\left( {c.g.c} \right)\)
\( \Rightarrow \widehat {OAD} = \widehat {OBC}\) (hai góc tương ứng)
* Xét \(\Delta OBF\) và \(\Delta OAE\) có:
+ \(OB = OA\,\left( {gt} \right)\)
+ \(\widehat {OBF} = \widehat {OAE}\) (cmt)
+ \(BF = AE\left( {gt} \right)\)
\( \Rightarrow \Delta OBF = \Delta OAE\left( {c.g.c} \right)\)
\( \Rightarrow OF = OE\) (hai cạnh tương ứng) và \(\widehat {BOF} = \widehat {AOE}\) (hai góc tương ứng)
Mà \(\widehat {BOF} + \widehat {FOA} = 180^\circ \) (hai góc kề bù) nên \(\widehat {AOE} + \widehat {FOA} = 180^\circ \)
Suy ra ba điểm \(F;\,O;E\) thẳng hàng và \(OE = OF\) nên \(O\) là trung điểm của \(EF \Rightarrow EF = 2.OE = 2.5 = 10\,cm.\)

