Chọn câu đúng.

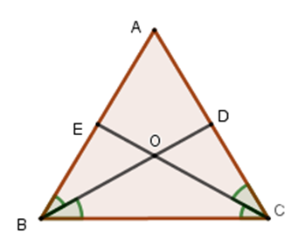
Vì $BD$ và $CE$ là tia phân giác của góc $\widehat {ABC}$ và $\widehat {ACB}$ nên $\widehat {ABD} = \widehat {CBD}$ và $\widehat {ACE} = \widehat {BCE}.$ 

Xét tam giác $ABD$ và tam giác $CBD$ có:

+ $AB = AC\,\left( {gt} \right)$

+ $\widehat {ABD} = \widehat {CBD}$ (cmt)

+ Cạnh $BD$ chung

Suy ra $\Delta ABD = \Delta CBD\,\left( {c - g - c} \right)$

$\Rightarrow \widehat {ADB} = \widehat {BDC}$ (hai góc tương ứng); $DC = AD$ (hai cạnh tương ứng) nên C sai.

Mà $\widehat {ADB} + \widehat {CDB} = 180^\circ$ (hai góc kề bù)

Nên $\widehat {ADB} = \widehat {CDB} = \dfrac{{180^\circ }}{2} = 90^\circ$ . Do đó $BD \bot AC.$

Tương tự ta có $CE \bot AB.$