Nếu \(\widehat A = {60^ \circ }\), thì số đo góc $K$ là:
Do \(\Delta ABD = \Delta KIH\) (theo câu trước), nên \(\widehat K = \widehat A = 60^\circ \) (hai góc tương ứng bằng nhau).
Phát biểu nào trong các phát biểu sau đây là đúng:
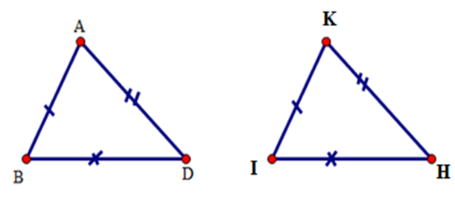
Xét tam giác $ABD$ và tam giác $KIH$ có:
$AB = KI,AD = KH,DB = IH.$
Do đó \(\Delta ABD = \Delta KIH\)(c.c.c).
Phát biểu nào trong các phát biểu sau đây là đúng:

Xét tam giác $ABD$ và tam giác $KIH$ có:
$AB = KI,AD = KH,DB = IH.$
Do đó \(\Delta ABD = \Delta KIH\)(c.c.c).
So sánh hai góc \(\widehat {CAC'};\,\widehat {CBC'}\)?
Vì \(\Delta ACB = \Delta BC'A\,\)(ý trước) ta suy ra \(\widehat {CAB} = \widehat {C'BA}\) và \(\widehat {C'AB} = \widehat {CBA}\) (1) (hai góc tương ứng bằng nhau)
Lại có \(\widehat {CAB} = \widehat {CAC'} + \widehat {C'AB}\) và \(\widehat {C'AB} = \widehat {CBC'} + \widehat {CBA}\) (tia làm giữa hai tia)
Suy ra $\widehat {CAC'} = \widehat {CAB} - \widehat {C'AB}$ và \(\widehat {CBC'} = \widehat {C'BA} - \widehat {CBA}\) (2)
Từ \(\left( 1 \right);\left( 2 \right)\) suy ra \(\widehat {CAC'} = \widehat {CBC'}\).
Chọn câu đúng.
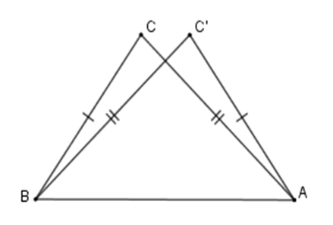
Hai tam giác \(ACB\) và \(BC'A\) có
$AC = BC'$ (gt)
\(BC = AC'\) (gt)
\(AB\) là cạnh chung
Nên \(\Delta ACB = \Delta BC'A\,\left( {c - c - c} \right).\)
Suy ra \(\widehat {BCA} = \widehat {BC'A}\) (hai góc tương ứng bằng nhau).
Nên A, B, C sai, D đúng.
Chọn câu đúng.

Hai tam giác \(ACB\) và \(BC'A\) có
$AC = BC'$ (gt)
\(BC = AC'\) (gt)
\(AB\) là cạnh chung
Nên \(\Delta ACB = \Delta BC'A\,\left( {c - c - c} \right).\)
Suy ra \(\widehat {BCA} = \widehat {BC'A}\) (hai góc tương ứng bằng nhau).
Nên A, B, C sai, D đúng.
Cho hình vẽ sau. Tam giác nào bằng với tam giác \(ABC?\)

Xét \(\Delta ABC\) và \(\Delta ADC\) có:
\(AB = AD\,\,(gt)\)
\(BC = DC\,\,(gt)\)
\(AC\) cạnh chung
\( \Rightarrow \Delta ABC = \Delta ADC\,\left( {c - c - c} \right).\)
Cho hình vẽ. Phát biểu nào sau đây là sai:

Xét \(\Delta ABH\) và \(\Delta ACH\) có:
\(AB = AC\left( {gt} \right)\)
\(AH\) cạnh chung
\(BH = CH\,\left( {gt} \right)\)
\( \Rightarrow \Delta ABH = \Delta ACH\,\left( {c.c.c} \right)\)
\( \Rightarrow \widehat {ABH} = \widehat {ACH},\widehat {BAH} = \widehat {CAH},\widehat {AHB} = \widehat {AHC}\) (các góc tương ứng).
Vậy đáp án D là sai.
Cho hình dưới đây.
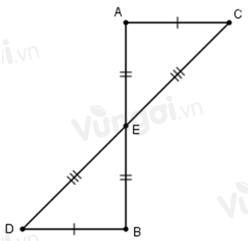
Chọn câu đúng nhất.
Xét \(\Delta AEC\) và \(\Delta BED\) có:
\(AE = BE\,\,(gt)\)
\(CE = DE\,\,(gt)\)
\(AC = BD\,\,(gt)\)
\( \Rightarrow \Delta AEC = \Delta BED\,\,\left( {c.c.c} \right)\)
\( \Rightarrow \widehat {AEC} = \widehat {BED};\,\widehat {ACE} = \widehat {BDE}\) (các góc tương ứng)
Mặt khác hai góc \(\widehat {ACE}\) và \(\widehat {BDE}\) ở vị trí so le trong nên \(AC//BD.\)

Nếu \(\widehat A = {45^ \circ }\), thì số đo \(\widehat D\) là:
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
\(\begin{array}{l}AB = DE\,\,(gt)\\BC = EF\,\,(gt)\\AC = DF\,(gt)\end{array}\)
\( \Rightarrow \Delta ABC = \Delta DEF\,\)(c.c.c).
\( \Rightarrow \widehat A = \widehat D = 45^\circ \) (hai góc tương ứng bằng nhau).
Phát biểu nào trong các phát biểu sau đây là đúng:
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
\(\begin{array}{l}AB = DE\,\,(gt)\\BC = EF\,\,(gt)\\AC = DF\,(gt)\end{array}\)
\( \Rightarrow \Delta ABC = \Delta DEF\,\)(c.c.c).
Phát biểu nào trong các phát biểu sau đây là đúng:
Xét \(\Delta ABC\) và \(\Delta DEF\) có:
\(\begin{array}{l}AB = DE\,\,(gt)\\BC = EF\,\,(gt)\\AC = DF\,(gt)\end{array}\)
\( \Rightarrow \Delta ABC = \Delta DEF\,\)(c.c.c).
Cho đoạn thẳng \(BC = 10cm.\) Trên một nửa mặt hẳng bờ \(BC\) vẽ tam giác \(ABC\) sao cho \(AC = 6cm,\) \(AB = 8cm,\) trên nửa mặt phẳng còn lại vẽ tam giác \(DBC\) sao cho \(BD = 6cm,\) \(CD = 8cm.\) Chọn câu đúng.
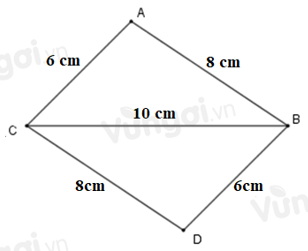
Từ bài ra ta có: \(AC = DB = 6\,cm;\,AB = DC = 8\,cm.\)
Xét \(\Delta ABC\) và \(\Delta DCB\) có:
\(AC = DB\,\left( {cmt} \right)\)
\(AB = DC\,\left( {cmt} \right)\)
\(BC\) cạnh chung
\( \Rightarrow \Delta ABC = \Delta DCB\,\left( {c - c - c} \right).\)
Cho \(\Delta AMN\) có \(AM = AN\) và \(I\) là trung điểm \(MN.\) Chọn câu đúng nhất.
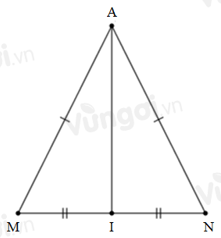
Xét \(\Delta AIM\) và \(\Delta AIN\) có:
\(AM = AN\,\left( {gt} \right)\)
\(IM = IN\) (vì \(I\) là trung điểm của \(MN\))
\(AI\) cạnh chung
\( \Rightarrow \Delta AIM = \Delta AIN\,\left( {c - c - c} \right)\)
\( \Rightarrow \widehat {AIM} = \widehat {AIN}\) và \(\widehat {AMI} = \widehat {ANI}\) (hai góc tương ứng bằng nhau)
Mặt khác \(\widehat {AIM} + \widehat {AIN} = 180^\circ \) (hai góc kề bù)
\( \Rightarrow \widehat {AIM} = \widehat {AIN} = \dfrac{{180^\circ }}{2} = 90^\circ .\) Hay \(AI \bot MN.\)
Vậy A, B, C đều đúng.
Cho tam giác \(MNP\) có MN = MP. Gọi \(K\) là trung điểm của \(NP.\) Biết \(\widehat {NMP} = {50^0}\) thì số đo góc \(MPN\) là:
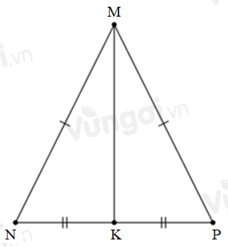
Xét \(\Delta MKN\) và \(\Delta MKP\) có:
\(MN = MP\,\,(gt)\)
\(KN = KP\) (vì \(K\) là trung điểm của \(NP\))
\(AK\) cạnh chung
\( \Rightarrow \Delta MKN = \Delta MKP\,\,\left( {c - c - c} \right).\)
\( \Rightarrow \widehat {MNK} = \widehat {MPK}\) (hai góc tương ứng)
Ta có: \(\widehat {MNK} = \widehat {MPK}\) (cmt), xét \(\Delta MNP\) có:
\(\widehat {NMP} + \widehat {MPN} + \widehat {PNM} = {180^0}\)
\( \Rightarrow 2\widehat {MPN} + \widehat {NMP} = {180^0}\)
\( \Rightarrow \widehat {MPN} = \left( {{{180}^0} - \widehat {NMP}} \right):2 = \left( {{{180}^0} - {{50}^0}} \right):2 = {65^0}.\)
Cho tam giác \(ABC{\rm{ }}\left( {AB < AC} \right).\) Trên tia \(AB\) lấy điểm \(D\) sao cho \(AD = AC.{\rm{ }}E\) là trung điểm của \(DC.\) Từ \(B\) vẽ \(BK\) vuông góc với \(CD.\) Chọn câu đúng.

Xét \(\Delta ADE\) và \(\Delta ACE\) có:
\(AD = AC\left( {gt} \right)\)
\(DE = CE\) (vì \(E\) là trung điểm của \(DC\))
\(AE\) cạnh chung
\( \Rightarrow \Delta ADE = \Delta ACE\,\,(c.c.c)\)
\( \Rightarrow \widehat {AED} = \widehat {AEC}\) (hai góc tương ứng bằng nhau).
Mặt khác \(\widehat {AED} + \widehat {AEC} = {180^o}\) (hai góc kề bù)
\( \Rightarrow \widehat {AED} = \widehat {AEC} = {180^o}:2 = {90^o}\)
Hay \(AE\, \bot CD\) (1)
Theo đề bài \(BK \bot CD\) (2)
Từ (1) và (2) suy ra \(AE//BK\).
Cho \(\widehat {xOy} = {60^0}\), vẽ cung tròn tâm O bán kính bằng 3cm, cung tròn này cắt Ox, Oy lần lượt ở A và B. Vẽ các cung tròn tâm A và tâm B có bán kính 4cm, chúng cắt nhau tại điểm C nằm trong góc xOy. Tính \(\widehat {xOC}\).

Xét \(\Delta OAC\) và \(\Delta OBC\) có:
\(OA = OB = 3cm\)
\(OC\) cạnh chung
\(AC = BC = 4cm\)
\( \Rightarrow \Delta OAC = \Delta OBC\,\,(c.c.c)\)
\( \Rightarrow \widehat {AOC} = \widehat {BOC}\) (hai góc tương ứng).
Mà \(\widehat {AOC} + \widehat {BOC} = {60^0}\) nên \(\widehat {AOC} = \widehat {BOC} = \dfrac{{{{60}^0}}}{2} = {30^0}.\)
Vậy \(\widehat {xOC} = {30^0}\).
Nếu \(C\) và \(D\) nằm cùng phía đối với \(AB\left( {C \ne D} \right).\) Chọn câu đúng.

Xét \(\Delta ACD\) và \(\Delta BCD\) có:
\(AC = BC\,\,(gt)\)
\(AD = BD\,(gt)\)
\(CD\) cạnh chung
\( \Rightarrow \Delta ACD = \Delta BCD\,\,(c.c.c)\)
\( \Rightarrow \widehat {ACD} = \widehat {BCD}\) (hai góc tương ứng bằng nhau).
Do đó \(CD\) là tia phân giác của \(\widehat {ACB}.\)
Hai điểm \(C\) và \(D\) nằm khác phía đối với \(AB\). Chọn khẳng định đúng.
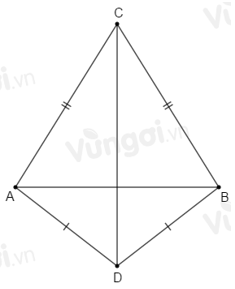
Xét \(\Delta ACD\) và \(\Delta BCD\) có:
\(AC = BC\,\,(gt)\)
\(AD = BD\,(gt)\)
\(CD\) cạnh chung
\( \Rightarrow \Delta ACD = \Delta BCD\,\,(c.c.c)\)
\( \Rightarrow \widehat {ACD} = \widehat {BCD}\) (hai góc tương ứng bằng nhau).
Do đó \(CD\) là tia phân giác của \(\widehat {ACB}.\)
Hai điểm \(C\) và \(D\) nằm khác phía đối với \(AB\). Chọn khẳng định đúng.

Xét \(\Delta ACD\) và \(\Delta BCD\) có:
\(AC = BC\,\,(gt)\)
\(AD = BD\,(gt)\)
\(CD\) cạnh chung
\( \Rightarrow \Delta ACD = \Delta BCD\,\,(c.c.c)\)
\( \Rightarrow \widehat {ACD} = \widehat {BCD}\) (hai góc tương ứng bằng nhau).
Do đó \(CD\) là tia phân giác của \(\widehat {ACB}.\)

