Trả lời bởi giáo viên
Đáp án đúng: a
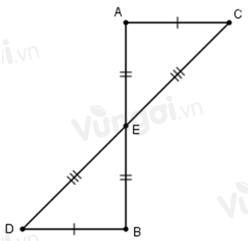
Xét ΔAEC và ΔBED có:
AE=BE(gt)
CE=DE(gt)
AC=BD(gt)
⇒ΔAEC=ΔBED(c.c.c)
⇒^AEC=^BED;^ACE=^BDE (các góc tương ứng)
Mặt khác hai góc ^ACE và ^BDE ở vị trí so le trong nên AC//BD.
Hướng dẫn giải:
- Áp dụng trường hợp bằng nhau thứ nhất của tam giác: Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
- Sử dụng dấu hiệu nhận biết hai đường thẳng song song: Nếu đường thẳng c cắt hai đường thẳng a,b tạo ra cặp góc so le trong bằng nhau (hoặc đồng vị bằng nhau, hoặc trong cùng phía bù nhau) thì a//b.
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
