Tổng ba góc của một tam giác

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta MNP$, ta có:

$\widehat M + \widehat N + \widehat P = {180^o}$

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta ABC$, ta có:

$\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat A = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - {90^o} = {90^o}.\end{array}$

Vậy $\Delta ABC$ là tam giác vuông.

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta ABC$, ta có:

$\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat A = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - \left( {{{87}^o} + {{67}^o}} \right) = {26^o}.\end{array}$.

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta MNP$, ta có:

$\begin{array}{l}\widehat M + \widehat N + \widehat P = {180^o}\\ \Rightarrow x + {50^o} + x = {180^o}\\ \Rightarrow 2x = {180^o} - {50^o}\\ \Rightarrow 2x = {130^o}\\ \Rightarrow x = {130^o}:2 = {65^o}.\end{array}$.

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta ABC$, ta có:

$\widehat A + \widehat B + \widehat C = {180^o}$

Mà $\widehat B = \widehat C\,\,\,(gt)$ nên $\widehat A + \widehat B + \widehat B = {180^o} \Rightarrow \widehat A + 2\widehat B = {180^o}$

$\Rightarrow {90^o} + 2\widehat B = {180^o} \Rightarrow 2\widehat B = {180^o} - {90^o}$

$\Rightarrow \widehat B = {90^o}:2 = {45^o}.$

Ta có: $\widehat {EDt}$ là góc ngoài tại đỉnh $D$ của $\Delta DEK$ nên $y = \widehat {EDt} = \widehat {DEK} + \widehat {DKE} = {60^o} + {40^o} = {100^o}.$

Ta có: $\widehat {EKD}$ và $\widehat {DKz}$ là hai góc kề bù nên $\widehat {EKD} + \widehat {DKz} = {180^o} \Rightarrow x = \widehat {DKz} = {180^o} - {40^o} = {140^o}.$

Áp dụng định lí tổng ba góc của tam giác vào $\Delta ABC$, ta có: $\widehat A + \widehat B + \widehat C = {180^0}.$

Theo đề bài ta có: $\dfrac{{\widehat A}}{3} = \dfrac{{\widehat B}}{4} = \dfrac{{\widehat C}}{5}.$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\begin{array}{l}\dfrac{{\widehat A}}{3} = \dfrac{{\widehat B}}{4} = \dfrac{{\widehat C}}{5} = \dfrac{{\widehat A + \widehat B + \widehat C}}{{3 + 4 + 5}} = \dfrac{{{{180}^0}}}{{12}} = {15^o}.\\ + )\,\dfrac{{\widehat A}}{3} = {15^o} \Rightarrow \widehat A = {3.15^o} = {45^o}\\ + )\,\dfrac{{\widehat B}}{4} = {15^o} \Rightarrow \widehat B = {4.15^o} = {60^o}\\ + )\,\dfrac{{\widehat C}}{5} = {15^o} \Rightarrow \widehat C = {5.15^o} = {75^o}\end{array}$

Vậy các góc của tam giác ABC là: $\widehat A = {45^0};\,\widehat B = {60^0};\,\widehat C = {75^0}.$

Áp dụng định lí tổng ba góc của tam giác vào $\Delta ABC$, ta có:

 $\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow \widehat B + \widehat C = {180^o} - {70^o}\\ \Rightarrow \widehat B + \widehat C = {110^o}\,\,\,\,\,(\,1\,)\end{array}$

Theo đề bài ta có: $\widehat B - \widehat C = {10^o} \Rightarrow \widehat B = \widehat C + {10^o}$    (2)

Thay (2) vào (1) ta được:

$\begin{array}{l}\widehat C + {10^o} + \widehat C = {110^o}\\ \Rightarrow 2\widehat C + {10^o} = {110^o}\\ \Rightarrow 2\widehat C = {110^o} - {10^o}\\ \Rightarrow 2\widehat C = {100^o}\\ \Rightarrow \widehat C = {100^o}:2 = {50^o}\,\\ \Rightarrow \widehat B = {50^o} + {10^o} = {60^o}\end{array}$.

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta ABC$, ta có:

 $\begin{array}{l}\widehat {BAC} + \widehat B + \widehat C = 180^\circ \\ \Rightarrow \widehat {BAC} = {180^o} - \left( {\widehat B + \widehat C} \right)\\ \Rightarrow \widehat {BAC} = {180^o} - \left( {{{70}^o} + {{30}^o}} \right) = {80^o}\end{array}$

Vì $AD$ là tia phân giác của $\widehat {BAC}$ nên $\widehat {BAD} = \widehat {CAD} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{80}^o}}}{2} = {40^o}$

Ta có: $\widehat {ADC}$ là góc ngoài tại đỉnh $D$ của tam giác $ABD$ nên ta có:

$\widehat {ADC} = \widehat B + \widehat {BAD} = {70^o} + {40^o} = {110^o}$.

Vậy $\widehat {ADC} = {110^o}.$

Áp dụng định lý tổng ba góc của một tam giác vào $\Delta ABC$, ta có:

$\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow \widehat B + \widehat C = 180^\circ  - \widehat A\\ \Rightarrow \widehat B + \widehat C = 180^\circ  - {60^o}\\ \Rightarrow \widehat B + \widehat C = {120^o}\,\,\,\,(\,1\,)\end{array}$

Lại có: $\widehat B = \dfrac{1}{2}\widehat C\,\,\,(\,2\,)$

Thay (2) vào (1) ta có:

 $\begin{array}{l}\dfrac{1}{2}\widehat C + \widehat C = {120^o}\\ \Rightarrow \dfrac{3}{2}\widehat C = {120^o}\\ \Rightarrow \widehat C = {120^o}:\dfrac{3}{2} = {80^o}\\ \Rightarrow \widehat B = \dfrac{1}{2}{.80^o} = {40^o}.\end{array}$.

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta IEC$, ta có:

$\begin{array}{l}\widehat {ICE} + \widehat {IEC} + \widehat {EIC} = {180^o}\\ \Rightarrow \widehat {ICE} = {180^o} - \left( {\widehat {IEC} + \widehat {EIC}} \right)\\ \Rightarrow \widehat {ICE} = {180^o} - \left( {{{90}^o} + {{55}^o}} \right) = {35^o}\end{array}$

Hay $\widehat {ACF} = {35^o}.$

Áp dụng định lí tổng ba góc của một tam giác vào $\Delta ACF$, ta có:

$\begin{array}{l}\widehat {ACF} + \widehat {AFC} + \widehat {FAC} = {180^o}\\ \Rightarrow \widehat {FAC} = {180^o} - \left( {\widehat {ACF} + \widehat {AFC}} \right)\\ \Rightarrow \widehat {FAC} = {180^o} - \left( {{{35}^o} + {{90}^o}} \right) = {55^o}.\end{array}$

Vậy $\widehat A = {55^o}.$

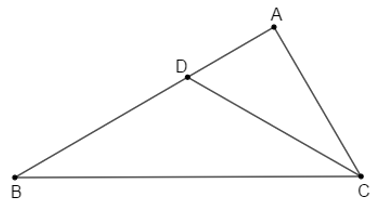
Áp dụng định lí tổng ba góc của một tam giác vào $\Delta ABC$, ta có:

$\widehat A + \widehat B + \widehat C = {180^o}$

$\Rightarrow \widehat B + \widehat C + \widehat B + \widehat C = {180^o}$  (vì $\widehat B + \widehat C = \widehat A$)

$\Rightarrow 2\left( {\widehat B + \widehat C} \right) = {180^o}$

$\Rightarrow \widehat B + \widehat C = {180^o}:2 = {90^o}$

Mặt khác $\widehat C = 2\widehat B\,\,(gt)$ nên $\widehat B + 2\widehat B = {90^o} \Rightarrow 3\widehat B = {90^o} \Rightarrow \widehat B = {90^o}:3 = {30^o}$.

$\Rightarrow \widehat C = {90^o} - {30^o} = {60^o}$

Vì $CD$ là phân giác của $\widehat {ACB}$ nên $\widehat {ACD} = \widehat {BCD} = \dfrac{{\widehat {ACB}}}{2} = \dfrac{{{{60}^o}}}{2} = {30^o}.$

$\widehat {ADC}$ là góc ngoài tại đỉnh $D$ của $\Delta BCD$ nên ta có:

$\widehat {ADC} = \widehat B + \widehat {BCD} = {30^o} + {30^o} = {60^o}.$

$\widehat {ADC}$ và $\widehat {BDC}$ là hai góc kề bù nên $\widehat {ADC} + \widehat {BDC} = {180^o}$

$\Rightarrow \widehat {BDC} = {180^o} - \widehat {ADC} = {180^o} - {60^o} = {120^o}.$

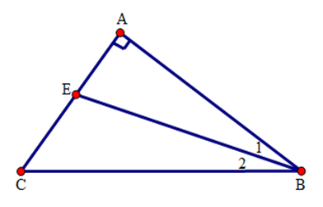
Góc $BEC$  là góc ngoài ở đỉnh $E$  của tam giác $AEC$ nên $\widehat {BEC} = \widehat A + \widehat {ABE} = {90^ \circ } + \widehat {ABE} > {90^ \circ }$

Vậy góc $BEC$ là góc tù nên $\widehat {BEC} > \widehat {EBA}$ và $\widehat {BEC} > \widehat {ECB}.$

Vậy A, C, D đúng, B sai.

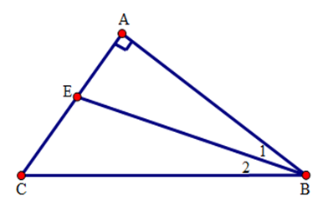
Theo giả thiết $\widehat C - \widehat B = {26^0}$.

Mặt khác do tam giác $ABC$  vuông tại $A$  nên $\widehat B + \widehat C = {90^ \circ }$

Từ đó ta có $\widehat C = \dfrac{{90^\circ  + 26^\circ }}{2} = {58^0} \Rightarrow \widehat B = {32^0}$.

Do $BE$  là tia phân giác của góc $ABC$  nên $\widehat {{B_1}} = \widehat {{B_2}} = {16^0}$

Sử dụng tinh chất góc ngoài của tam giác ta tìm được $\widehat {AEB} = \widehat C + \widehat {{B_2}} = {58^0} + 16^\circ  = 74^\circ .$

Và $\widehat {BEC} = \widehat A + \widehat {{B_1}} = 106^\circ .$

Vậy $\widehat {AEB} = 74^\circ ;\,\widehat {BEC} = 106^\circ .$

Góc $BEC$  là góc ngoài ở đỉnh $E$  của tam giác $AEC$ nên $\widehat {BEC} = \widehat A + \widehat {ABE} = {90^ \circ } + \widehat {ABE} > {90^ \circ }$

Vậy góc $BEC$ là góc tù nên $\widehat {BEC} > \widehat {EBA}$ và $\widehat {BEC} > \widehat {ECB}.$

Vậy A, C, D đúng, B sai.

Góc $BEC$  là góc ngoài ở đỉnh $E$  của tam giác $AEC$ nên $\widehat {BEC} = \widehat A + \widehat {ABE} = {90^ \circ } + \widehat {ABE} > {90^ \circ }$

Vậy góc $BEC$ là góc tù nên $\widehat {BEC} > \widehat {EBA}$ và $\widehat {BEC} > \widehat {ECB}.$

Vậy A, C, D đúng, B sai.

Tổng ba góc của một tam giác bằng $180^\circ .$

Vì tam giác $ABC$ vuông tại $A$ nên $\widehat B + \widehat C = 90^\circ$.

Xét tam giác $ABC$  có :$\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B = {180^0} - \left( {\widehat A + \widehat C} \right) = {180^0} - \left( {{{96}^0} + {{50}^0}} \right) = {34^0}$.

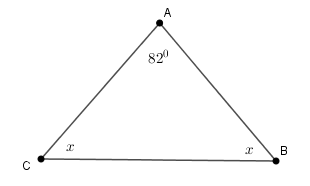
Xét tam giác $ABC$  có :$\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B + \widehat C = {180^0} - \widehat A = {180^0} - {82^0} = {98^0}$.

Hay $x + x = {98^0} \Rightarrow 2x = {98^0} \Rightarrow x = {49^0}$