\(\widehat C - \widehat B = {26^0}\). Tính \(\widehat {AEB}\) và $\widehat {BEC}$.

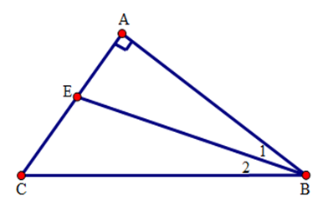
Theo giả thiết \(\widehat C - \widehat B = {26^0}\).

Mặt khác do tam giác $ABC$  vuông tại $A$  nên \(\widehat B + \widehat C = {90^ \circ }\)

Từ đó ta có \(\widehat C = \dfrac{{90^\circ  + 26^\circ }}{2} = {58^0} \Rightarrow \widehat B = {32^0}\).

Do $BE$  là tia phân giác của góc $ABC$  nên \(\widehat {{B_1}} = \widehat {{B_2}} = {16^0}\)

Sử dụng tinh chất góc ngoài của tam giác ta tìm được \(\widehat {AEB} = \widehat C + \widehat {{B_2}} = {58^0} + 16^\circ  = 74^\circ .\)

Và \(\widehat {BEC} = \widehat A + \widehat {{B_1}} = 106^\circ .\)

Vậy \(\widehat {AEB} = 74^\circ ;\,\widehat {BEC} = 106^\circ .\)