Tính số đo góc \(DBK.\)
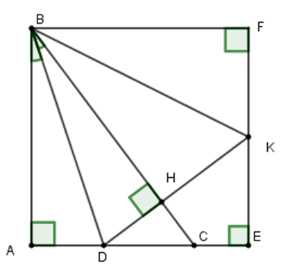
+ Qua \(B\) kẻ đường thẳng vuông góc với \(EK\) cắt \(EK\) tại \(F\)
Khi đó ta có \(ABFE\) là hình vuông nên \(\widehat {ABF} = 90^\circ \) và \(AB = BF\)
Lại có \(AB = BH\) (ý trước) nên \(BH = BF\)
Xét hai tam giác vuông \(BHK\) và \(BFK\) có \(BH = BF\left( {cmt} \right);\,BK\) cạnh chung
Nên \(\Delta BHK = \Delta BFK\left( {ch - cgv} \right)\)\( \Rightarrow \widehat {FBK} = \widehat {HBK}\)
Lại có \(\widehat {ABD} = \widehat {DBH}\) (do \(BD\) là phân giác góc \(\widehat {ABC}\) )
Nên \(\widehat {DBH} + \widehat {HBK} = \widehat {ABD} + \widehat {KBF} = \dfrac{{\widehat {DBH} + \widehat {HBK} + \widehat {ABD} + \widehat {KBF}}}{2}\)\(\dfrac{{\widehat {ABF}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Mà Vậy \(\widehat {DBK} = \widehat {DBH} + \widehat {HBK} = 45^\circ .\)
Chọn câu đúng.
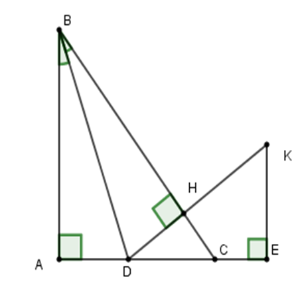
Xét hai tam giác vuông \(BAD\) và \(BHD\) có \(\widehat A = \widehat H = 90^\circ ;\,\widehat {ABD} = \widehat {HBD}\) (vì \(BD\) là tia phân giác góc \(B\)) và cạnh \(BD\) chung
\( \Rightarrow \Delta ABD = \Delta HBD\left( {ch - gn} \right)\) \( \Rightarrow BA = BH\) (hai cạnh tương ứng).
Chọn câu đúng.

Xét hai tam giác vuông \(BAD\) và \(BHD\) có \(\widehat A = \widehat H = 90^\circ ;\,\widehat {ABD} = \widehat {HBD}\) (vì \(BD\) là tia phân giác góc \(B\)) và cạnh \(BD\) chung
\( \Rightarrow \Delta ABD = \Delta HBD\left( {ch - gn} \right)\) \( \Rightarrow BA = BH\) (hai cạnh tương ứng).
Cho tam giác \(DEF\) và tam giác \(JIK\) có \(EF = IK;\,\widehat D = \widehat J = 90^\circ \). Cần thêm một điều kiện gì để \(\Delta DEF = \Delta JIK\) theo trường hợp cạnh huyền-cạnh góc vuông?
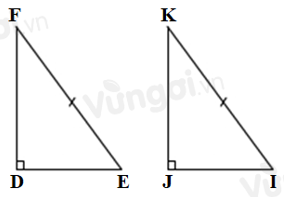
Ta có: tam giác \(DEF\) và tam giác \(JIK\) có \(EF = IK;\,\widehat D = \widehat J = 90^\circ \) mà \(EF;IK\) là hai cạnh huyền của hai tam giác \(DEF\) và \(JIK\) nên để hai tam giác bằng nhau theo trường hợp cạnh huyền - cạnh góc vuông thì ta cần thêm hai cạnh góc vuông bằng nhau là \(DE = JI\) hoặc \(DF = JK\).
Cho tam giác \(PQR\) và tam giác \(TUV\) có \(\widehat P = \widehat T = {90^0},\,\widehat Q = \widehat U\). Cần thêm một điều kiện gì để tam giác \(TUV\) và tam giác \(PQR\) bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề:
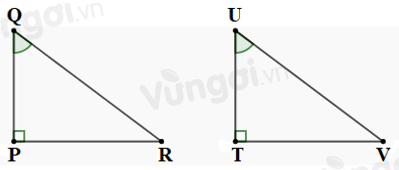
Ta có: \(\,\widehat Q = \widehat U\) mà \(\widehat Q\) và \(\widehat U\) là hai góc nhọn của hai tam giác \(PQR\) và \(TUV\).
Do đó, để tam giác vuông \(PQR\) và tam giác vuông \(TUV\) bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn \(\widehat Q\) và \(\widehat U\) của hai tam giác này bằng nhau, tức là bổ sung thêm điều kiện \(PQ = TU.\)
Cho tam gác ABC và tam giác DEF có: \(\widehat B = \widehat D = {90^0},\,\widehat A = \widehat E,\,\,AC = FE\). Tính độ dài \(AB\) biết \(DE = 5cm.\)
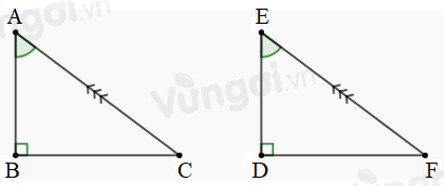
Xét hai tam giác vuông \(ABC\) và \(EDF\) có:
\(\widehat B = \widehat D = {90^0}\)
\(\widehat A = \widehat E\,(gt)\)
\(AC = EF\,(gt)\)
\( \Rightarrow \Delta ABC = \Delta EDF\) (cạnh huyền - góc nhọn)
\( \Rightarrow AB = ED = 5cm\) (hai cạnh tương ứng).
Cho tam giác \(MNP\) và tam giác \(KHI\) có: \(\widehat M = \widehat K = 90^\circ ;\,NP = HI;\,MN = HK\). Chọn khẳng định đúng.
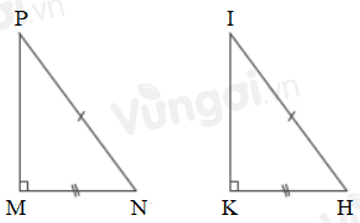
Xét hai tam giác vuông \(MNP\) và \(KHI\) có:
\(\widehat M = \widehat K = 90^\circ \)
\(\,NP = HI\,(gt)\)
\(MN = KH\,(gt)\)
\( \Rightarrow \Delta MNP = \Delta KHI\) (cạnh huyền - cạnh góc vuông).
Cho tam giác \(ABC\) và tam giác \(DEF\) có: \(AB = DE\), \(\widehat B = \widehat E\), \(\widehat A = \widehat D = 90^\circ \). Biết \(AB = 9cm; AC = 12cm.\) Độ dài \(EF\) là:
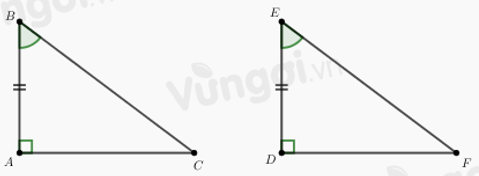
Áp dụng đinh lí Pytago vào tam giác vuông \(ABC\), ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2}\\ \Rightarrow B{C^2} = {9^2} + {12^2} = 225\\ \Rightarrow BC = \sqrt {225} = 15\,\left( {cm} \right)\end{array}\)
Xét hai tam giác vuông \(ABC\) và \(DEF\) có:
\(\begin{array}{l}AB = DE\;\;\left( {gt} \right)\\\,\widehat B = \widehat E\;\;\left( {gt} \right)\\\,\widehat A = \widehat D = {90^0}\end{array}\)
\( \Rightarrow \Delta ABC = \Delta DEF\) (cạnh góc vuông - góc nhọn kề).
\( \Rightarrow BC = EF = 15\,cm\) (hai cạnh tương ứng bằng nhau).
Cho tam giác \(DEF\) và tam giác \(HKI\) có: \(\widehat D = \widehat H = 90^\circ \), \(\widehat F = \widehat I\), \(DF = HI.\) Biết \(\widehat F = {55^0}\). Số đo góc \(K\) là:
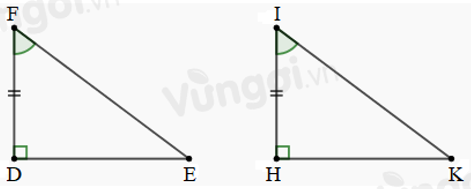
Áp dụng định lí tổng ba góc của một tam giác vào \(\Delta DEF\), ta có:
\(\widehat D + \widehat E + \widehat F = {180^o}\)
\( \Rightarrow \widehat E = {180^o} - \left( {\widehat D + \widehat F} \right)\)
\( \Rightarrow \widehat E = {180^o} - \left( {{{90}^o} + {{55}^o}} \right) = {35^o}\)
Xét hai tam giác vuông \(DEF\) và \(HKI\) có:
\(\begin{array}{l}\widehat D = \widehat H = {90^0}\\\widehat F = \widehat I\;\;\left( {gt} \right)\\DF = HI\;\;\left( {gt} \right)\end{array}\)
\( \Rightarrow \Delta DEF = \Delta HKI\) (cạnh góc vuông - góc nhọn kề).
\( \Rightarrow \widehat E = \widehat K = 35^\circ \) (hai góc tương ứng).
Cho hình vẽ sau với \(\widehat {{D_1}} = \widehat {{D_2}}\). Chọn câu sai.
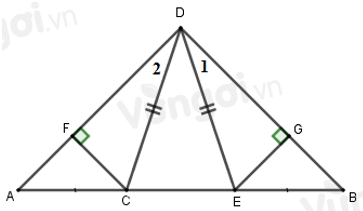
Vì tam giác \(CDE\) cân tại \(D\) (do \(DC = DE\)) nên \(\widehat {DCE} = \widehat {DEC}\) (tính chất tam giác cân) (1)
Lại có \(\widehat {DCA} + \widehat {DCE} = 180^\circ \) và \(\widehat {DEB} + \widehat {DEC} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {DCA} = 180^\circ - \widehat {DCE}\); \(\widehat {DEB} = 180^\circ - \widehat {DEC}\) (2)
Từ (1) và (2) suy ra: \(\widehat {DCA} = \widehat {DEB}.\)
Xét \(\Delta ACD\) và \(\Delta BED\) có:
\(DC = DE\,\, (gt)\)
\(\widehat {DCA} = \widehat {DEB}\left( {cmt} \right)\)
\(\widehat {{D_2}} = \widehat {{D_1}}\,\,(gt)\)
\( \Rightarrow \Delta ACD = \Delta BED\,\,(g.c.g)\)
\( \Rightarrow AD = BD\) (hai cạnh tương ứng).
Xét hai tam giác vuông \(DCF\) và \(DEG\) có:
\(\widehat {CFD} = \widehat {EGD} = 90^\circ \)
\(DC = DE\,(gt)\)
\(\widehat {{D_2}} = \widehat {{D_1}}\,\left( {cmt} \right)\)
\( \Rightarrow \Delta DCF = \Delta DEG\) (cạnh huyền – góc nhọn).
Ta có: \(\widehat {{D_1}} = \widehat {{D_2}}\,\,(gt)\)
\( \Rightarrow \widehat {{D_1}} + \widehat {CDE} = \widehat {{D_2}} + \widehat {CDE}\)
\( \Rightarrow \widehat {BDC} = \widehat {ADE}\)
Xét \(\Delta ADE\) và \(\Delta BDC\) có:
\(DE = DC\,\,(gt)\)
\(\widehat {ADE} = \widehat {BDC}\,\,(cmt)\)
\(\widehat {AED} = \widehat {BCD}\) (vì \(\Delta CDE\) cân tại \(D\))
\( \Rightarrow \Delta ADE = \Delta BDC\,\,(g.c.g)\)
Do đó đáp án D sai.
Cho tam giác \(ABC\) cân tại \(A\) có: \(AH \bot BC\) tại \(H.\) Tính số đo góc \(BAH\) biết \(\widehat {BAC} = {50^0}.\)
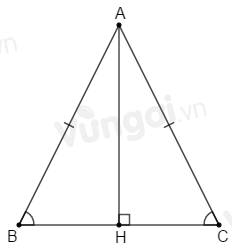
\(\Delta ABC\) cân tại \(A\), suy ra \(AB = AC;\,\,\widehat B = \widehat C\).
Xét hai tam giác vuông \(AHB\) và \(AHC\) có:
\(\widehat {AHB} = \widehat {AHC} = {90^o}\)
\(AB = AC\,\,(cmt)\)
\(\widehat B = \widehat C\,\,(cmt)\)
\( \Rightarrow \Delta AHB = \Delta AHC\,\) (cạnh huyền – góc nhọn).
\( \Rightarrow \widehat {BAH} = \widehat {CAH}\) (hai góc tương ứng).
Mặt khác: \(\widehat {BAH} + \widehat {CAH} = \widehat {BAC}\) suy ra \(\widehat {BAH} = \widehat {CAH} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{50}^o}}}{2} = {25^o}.\)
Cho tam giác \(ABC\) vuông cân tại \(A\), có \(AC = 8cm.\) Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) lần lượt vuông góc với \(d\) tại \(H;\,K.\) Khi đó tổng \(B{H^2} + C{K^2}\) bằng:
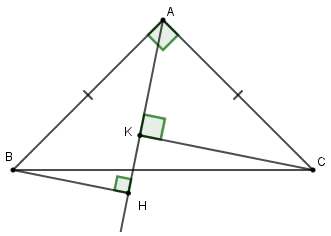
Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC\) (tính chất)
Lại có: \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì \(\Delta ABH\) vuông tại \(H\)) và \(\widehat {CAH} + \widehat {BAH} = 90^\circ \)
Suy ra \(\widehat {ABH} = \widehat {CAK}\) (cùng phụ với \(\widehat {BAH}\)).
Xét \(\Delta ABH\) và \(\Delta CAK\) có:
\(AB = CA\,\,(cmt)\)
\(\widehat {AHB} = \widehat {CKA} = {90^o}\)
\(\widehat {ABH} = \widehat {CAK}\,\,(cmt)\)
\( \Rightarrow \Delta ABH = \Delta CAK\) (cạnh huyền-góc nhọn)
\( \Rightarrow BH = AK\) (hai cạnh tương ứng).
Do đó \(B{H^2} + C{K^2} = A{K^2} + C{K^2}\,\,\left( 1 \right)\)
Áp dụng định lý Pytago vào tam giác vuông \(ACK\) có: \(A{K^2} + C{K^2} = A{C^2}\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra: \(B{H^2} + C{K^2} = A{C^2} = {8^2} = 64\).
Chọn câu đúng.
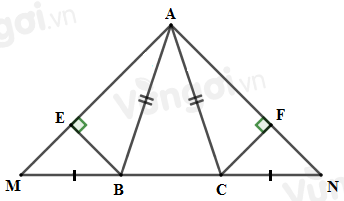
Sử dụng kết quả câu trước \(\Delta ABE = \Delta ACF\) nên \(BE = CF\) (hai cạnh tương ứng).
Xét hai tam giác vuông \(BME\) và \(CNF\) có:
\(\widehat {BEM} = \widehat {CFN} = {90^o}\)
\(BE = CF\,\,(cmt)\)
\(MB = NC\,\,(gt)\)
\( \Rightarrow \Delta BME = \Delta CNF\) (cạnh huyền – cạnh góc vuông).
So sánh \(BE\) và \(CF.\)
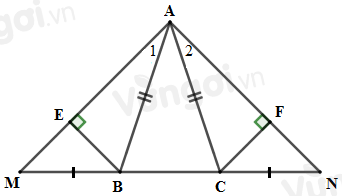
Sử dụng kết quả câu trước ta có \(\Delta ABM = \Delta ACN\,\,\) suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng).
Xét hai tam giác vuông \(ABE\) và \(ACF\) có:
\(\widehat {AEB} = \widehat {AFC} = {90^o}\)
\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))
\(\widehat {{A_1}} = \widehat {{A_2}}\,\,(cmt)\)
\( \Rightarrow \Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn)
\( \Rightarrow BE = CF\) (hai cạnh tương ứng).
Tam giác \(AMN\) là tam giác gì?
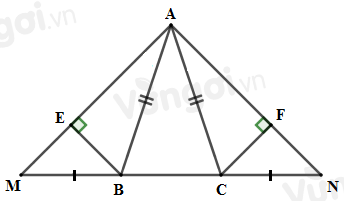
\(\Delta ABC\) cân tại \(A\) nên \(AB = AC,\,\widehat {ABC} = \widehat {ACB}\) (1)
Mặt khác: \(\widehat {ABM} + \widehat {ABC} = {180^o}\) (kề bù) (2)
\(\widehat {ACN} + \widehat {ACB} = {180^o}\) (kề bù) (3)
Từ (1), (2) và (3) suy ra \(\widehat {ABM} = \widehat {ACN}\).
Xét \(\Delta ABM\) và \(\Delta ACN\) có:
\(AB = AC\,\,(cmt)\)
\(\widehat {ABM} = \widehat {ACN}\,\,(cmt)\)
\(BM = CN\,\,(gt)\)
\( \Rightarrow \Delta ABM = \Delta ACN\,\,(c.g.c)\)
\( \Rightarrow AM = AN\) (hai cạnh tương ứng).
\( \Rightarrow \Delta AMN\) cân tại \(A.\)
Tam giác \(AMN\) là tam giác gì?

\(\Delta ABC\) cân tại \(A\) nên \(AB = AC,\,\widehat {ABC} = \widehat {ACB}\) (1)
Mặt khác: \(\widehat {ABM} + \widehat {ABC} = {180^o}\) (kề bù) (2)
\(\widehat {ACN} + \widehat {ACB} = {180^o}\) (kề bù) (3)
Từ (1), (2) và (3) suy ra \(\widehat {ABM} = \widehat {ACN}\).
Xét \(\Delta ABM\) và \(\Delta ACN\) có:
\(AB = AC\,\,(cmt)\)
\(\widehat {ABM} = \widehat {ACN}\,\,(cmt)\)
\(BM = CN\,\,(gt)\)
\( \Rightarrow \Delta ABM = \Delta ACN\,\,(c.g.c)\)
\( \Rightarrow AM = AN\) (hai cạnh tương ứng).
\( \Rightarrow \Delta AMN\) cân tại \(A.\)
Chọn câu đúng.

Xét hai tam giác vuông \(BAD\) và \(BHD\) có \(\widehat A = \widehat H = 90^\circ ;\,\widehat {ABD} = \widehat {HBD}\) (vì \(BD\) là tia phân giác góc \(B\)) và cạnh \(BD\) chung
\( \Rightarrow \Delta ABD = \Delta HBD\left( {ch - gn} \right)\) \( \Rightarrow BA = BH\) (hai cạnh tương ứng).
Cho tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \). Cần thêm một điều kiện gì để tam giác \(ABC\) và tam giác \(NPM\) bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông ?
Ta có tam giác \(ABC\) và tam giác \(NPM\) có \(BC = PM;\,\widehat B = \widehat P = 90^\circ \) mà \(BC;PM\) là hai cạnh góc vuông của hai tam giác \(ABC\) và \(NPM\) nên để hai tam giác bằng nhau theo trường hợp cạnh huyền-cạnh góc vuông thì ta cần thêm hai cạnh huyền bằng nhau là \(CA = MN.\)
Cho tam giác $ABC$ và tam giác $MNP$ có \(\widehat A = \widehat M = {90^0},\,\widehat C = \widehat P\). Cần thêm một điều kiện gì để tam giác $ABC$ và tam giác $MNP$ bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề:
Ta có: \(\,\widehat C = \widehat P\), mà góc $C$ và góc $P$ là hai góc nhọn kề của hai tam giác $ABC$ và $MNP$
Do đó: để tam giác vuông $ABC$ và tam giác vuông $MNP$ bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn \(\widehat C\) và \(\widehat P\) của hai tam giác này bằng nhau, tức là bổ sung thêm điều kiện \(AC = MP.\)
Cho tam gác $ABC$ và tam giác $DEF$ có \(\widehat B = \widehat E = {90^0},\,AC = DF,\,\,\widehat A = \widehat F\). Phát biểu nào trong các phát biểu sau đây là đúng
Xét tam giác $ABC$ và tam giác $FED$ có:
+ \(\widehat B = \widehat E = {90^0}\).
+ \(AC = DF\;\;\left( {gt} \right)\)
+ \(\,\,\widehat A = \widehat F\;\;\left( {gt} \right)\)
\( \Rightarrow \Delta ABC = \Delta FED\) (cạnh huyền - góc nhọn)

