Cho tam giác \(ABC\) và tam giác $KHI$ có: \(\widehat A = \widehat K = 90^\circ ;\,AB = KH;\,BC = HI\) . Phát biểu nào trong các phát biểu sau là đúng:
Xét tam giác $ABC$ và tam giác $KHI$ có:
\(\begin{array}{l}\widehat A = \widehat K = 90^\circ \\AB = KH\;\;\left( {gt} \right)\\BC = HI\;\;\;\left( {gt} \right)\end{array}\)
\( \Rightarrow \Delta ABC = \Delta KHI\) (cạnh huyền - cạnh góc vuông)
Cho tam giác $ABC$ và tam giác $DEF$ có $AB = DE$ , \(\widehat B = \widehat E\) , \(\widehat A = \widehat D = 90^\circ \). Biết $AC = 9cm.$ Độ dài $DF$ là:
Xét tam giác $ABC$ và tam giác $DEF$ có
\(AB = DE\;\;\left( {gt} \right);\,\widehat B = \widehat E\;\;\left( {gt} \right);\,\widehat A = \widehat D = {90^0}.\)
\( \Rightarrow \Delta ABC = \Delta DEF\)( cạnh góc vuông - góc nhọn) .
\( \Rightarrow DF = AC = 9\,cm\) (hai cạnh tương ứng bằng nhau)
Cho tam giác $DEF$ và tam giác $HKI$ có \(\widehat D = \widehat H = 90^\circ \), \(\widehat E = \widehat K\), $DE = HK.$ Biết \(\widehat F = {80^0}\). Số đo góc \(I\) là:
Xét tam giác $DEF$ và tam giác $HKI$ có
\(\widehat D = \widehat H = {90^0};\,\widehat E = \widehat K\;\;\left( {gt} \right);\,DE = HK\;\;\left( {gt} \right)\)
\( \Rightarrow \Delta DEF = \Delta HKI\) (cạnh góc vuông - góc nhọn).
\( \Rightarrow \widehat F = \widehat I = 80^\circ \) ( hai góc tương ứng)
Cho hình vẽ sau. Chọn câu đúng.
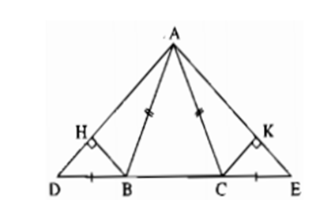
Vì tam giác \(ABC\) cân tại \(A\) (do \(AB = AC\) ) nên \(\widehat {ABC} = \widehat {ACB}\) (tính chất) (1)
Lại có \(\widehat {ABC} + \widehat {ABD} = 180^\circ \) và \(\widehat {ACB} + \widehat {ACE} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {ABD} = 180^\circ - \widehat {ABC}\) ; \(\widehat {ACE} = 180^\circ - \widehat {ACB}\) (2)
Từ (1) và (2) suy ra \(\widehat {ABD} = \widehat {ACE}\)
Xét tam giác \(ABD\) và tam giác \(ACE\) có
\(AB = AC;\,\)\(\widehat {ABD} = \widehat {ACE}\,\left( {cmt} \right);\)\(BD = CE\,\)
Suy ra \(\Delta ABD = \Delta ACE\left( {c - g - c} \right)\) \( \Rightarrow \widehat {DAB} = \widehat {CAE}\) (hai góc tương ứng)
Xét tam giác \(AHB\) và \(AKC\) có
+ \(\widehat H = \widehat K = 90^\circ \)
+ \(AB = AC\)
+ \(\widehat {DAB} = \widehat {CAE}\,\left( {cmt} \right)\)
Suy ra \(\Delta AHB = \Delta AKC\,\left( {ch - gn} \right)\)
Cho tam giác \(ABC\) có \(M\) là trung điểm của \(BC\) và \(AM\) là tia phân giác của góc \(A\). Khi đó, tam giác \(ABC\) là tam giác gì?
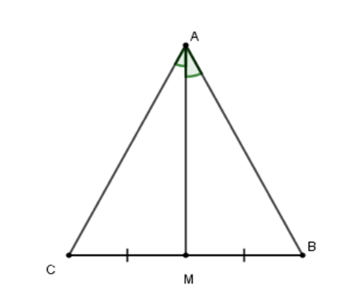
Tam giác \(ABC\) có \(AM\) vừa là đường trung tuyến vừa là đường phân giác nên \(\Delta BAC\) cân tại $A.$
Cho tam giác \(ABC\) vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) vuông góc với đường thẳng \(d.\) Khi đó tổng \(B{H^2} + C{K^2}\) bằng
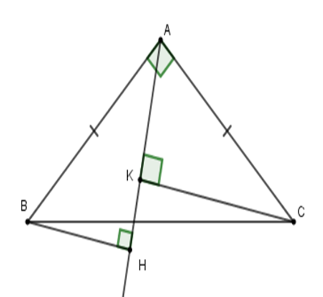
Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC\) (tính chất)
Lại có \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì \(\Delta ABH\) vuông tại \(H\) ) và \(\widehat {CAH} + \widehat {BAH} = 90^\circ \)
Nên \(\widehat {ABH} = \widehat {CAK}\) (cùng phụ với \(\widehat {BAH}\) )
\( \Rightarrow \Delta ABH = \Delta CAK\) (cạnh huyền-góc nhọn) suy ra \(BH = AK.\)
Do đó \(B{H^2} + C{K^2} = A{K^2} + C{K^2}\,\,\left( 1 \right)\)
Xét tam giác \(ACK\), theo định lý Pytago: \(A{K^2} + C{K^2} = A{C^2}\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(B{H^2} + C{K^2} = A{C^2}.\)
Cho tam giác \(ABC\) vuông tại \(A\)\(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\)
Chọn câu đúng.
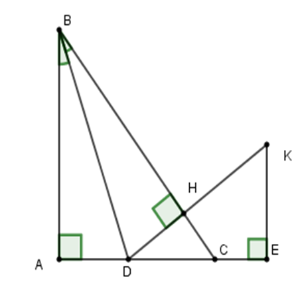
Xét hai tam giác vuông \(BAD\) và \(BHD\) có \(\widehat A = \widehat H = 90^\circ ;\,\widehat {ABD} = \widehat {HBD}\) (vì \(BD\) là tia phân giác góc \(B\)) và cạnh \(BD\) chung
\( \Rightarrow \Delta ABD = \Delta HBD\left( {ch - gn} \right)\) \( \Rightarrow BA = BH\) (hai cạnh tương ứng).
Cho tam giác \(ABC\) vuông tại \(A\)\(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\)
Tính số đo góc \(DBK.\)
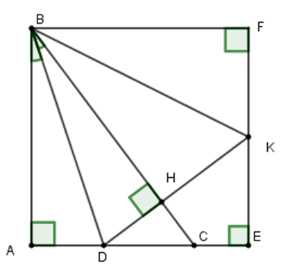
+ Qua \(B\) kẻ đường thẳng vuông góc với \(EK\) cắt \(EK\) tại \(F\)
Khi đó ta có \(ABFE\) là hình vuông nên \(\widehat {ABF} = 90^\circ \) và \(AB = BF\)
Lại có \(AB = BH\) (ý trước) nên \(BH = BF\)
Xét hai tam giác vuông \(BHK\) và \(BFK\) có \(BH = BF\left( {cmt} \right);\,BK\) cạnh chung
Nên \(\Delta BHK = \Delta BFK\left( {ch - cgv} \right)\)\( \Rightarrow \widehat {FBK} = \widehat {HBK}\)
Lại có \(\widehat {ABD} = \widehat {DBH}\) (do \(BD\) là phân giác góc \(\widehat {ABC}\) )
Nên \(\widehat {DBH} + \widehat {HBK} = \widehat {ABD} + \widehat {KBF} = \dfrac{{\widehat {DBH} + \widehat {HBK} + \widehat {ABD} + \widehat {KBF}}}{2}\)\(\dfrac{{\widehat {ABF}}}{2} = \dfrac{{90^\circ }}{2} = 45^\circ \)
Mà Vậy \(\widehat {DBK} = \widehat {DBH} + \widehat {HBK} = 45^\circ .\)
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\).
Tam giác \(AMN\) là tam giác gì?
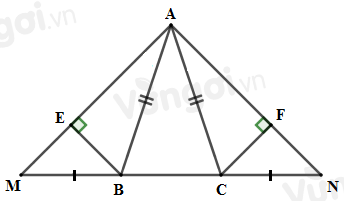
\(\Delta ABC\) cân tại \(A\) nên \(AB = AC,\,\widehat {ABC} = \widehat {ACB}\) (1)
Mặt khác: \(\widehat {ABM} + \widehat {ABC} = {180^o}\) (kề bù) (2)
\(\widehat {ACN} + \widehat {ACB} = {180^o}\) (kề bù) (3)
Từ (1), (2) và (3) suy ra \(\widehat {ABM} = \widehat {ACN}\).
Xét \(\Delta ABM\) và \(\Delta ACN\) có:
\(AB = AC\,\,(cmt)\)
\(\widehat {ABM} = \widehat {ACN}\,\,(cmt)\)
\(BM = CN\,\,(gt)\)
\( \Rightarrow \Delta ABM = \Delta ACN\,\,(c.g.c)\)
\( \Rightarrow AM = AN\) (hai cạnh tương ứng).
\( \Rightarrow \Delta AMN\) cân tại \(A.\)
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\).
So sánh \(BE\) và \(CF.\)
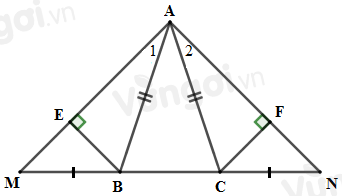
Sử dụng kết quả câu trước ta có \(\Delta ABM = \Delta ACN\,\,\) suy ra \(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng).
Xét hai tam giác vuông \(ABE\) và \(ACF\) có:
\(\widehat {AEB} = \widehat {AFC} = {90^o}\)
\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))
\(\widehat {{A_1}} = \widehat {{A_2}}\,\,(cmt)\)
\( \Rightarrow \Delta ABE = \Delta ACF\) (cạnh huyền – góc nhọn)
\( \Rightarrow BE = CF\) (hai cạnh tương ứng).
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(M,\) trên tia đối của tia \(CB\) lấy điểm \(N\) sao cho \(MB = NC.\) Kẻ \(BE \bot AM\,\left( {E \in AM} \right);CF \bot AN\,\left( {F \in AN} \right)\).
Chọn câu đúng.
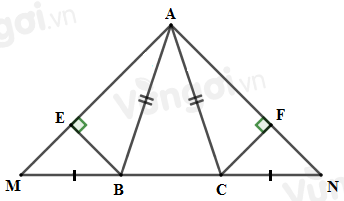
Sử dụng kết quả câu trước \(\Delta ABE = \Delta ACF\) nên \(BE = CF\) (hai cạnh tương ứng).
Xét hai tam giác vuông \(BME\) và \(CNF\) có:
\(\widehat {BEM} = \widehat {CFN} = {90^o}\)
\(BE = CF\,\,(cmt)\)
\(MB = NC\,\,(gt)\)
\( \Rightarrow \Delta BME = \Delta CNF\) (cạnh huyền – cạnh góc vuông).
Cho tam giác \(ABC\) vuông cân tại \(A\) và \(D\) là trung điểm \(AC.\) Từ \(A\) kẻ đường vuông góc với \(BD,\) cắt \(BC\) tại \(E.\) Chọn đáp án đúng.
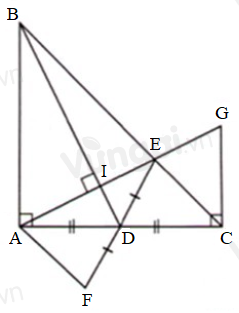
Từ \(C\) dựng đường thẳng vuông góc với \(AC\) cắt \(AE\) tại \(G\). Trên tia đối của tia \(DE\) lấy điểm \(F\) sao cho \(DE = DF\). Gọi \(I\) là giao điểm của \(AE\) và \(BD.\)
\(\Delta ABD\) vuông tại \(A\) nên \(\widehat {ABD} + \widehat {ADB} = {90^o}\)
\(\Delta AID\) vuông tại \(I\) nên \(\widehat {DAI} + \widehat {ADI} = {90^o}\)
Mà \(\widehat {ADB} = \widehat {ADI}\) nên \(\widehat {ABD} = \widehat {DAI}\) hay \(\widehat {ABD} = \widehat {CAG}\)
Xét \(\Delta ABD\) và \(\Delta CAG\) có:
\(\widehat {BAD} = \widehat {ACG} = {90^o}\)
\(AB = CA\) (vì \(\Delta ABC\) cân tại \(A\))
\(\widehat {ABD} = \widehat {CAG}\,\,(cmt)\)
\( \Rightarrow \Delta ABD = \Delta CAG\) (g.c.g).
\( \Rightarrow AD = CG\) (hai cạnh tương ứng).
Mà \(AD = CD\) (vì \(D\) là trung điểm của \(AC\)) nên \(CD = CG\)
\(\Delta ABC\) vuông cân tại \(A\) nên \(\widehat {ACB} = \dfrac{{{{180}^o} - \widehat A}}{2} = \dfrac{{{{180}^o} - {{90}^o}}}{2} = {45^o}\) hay \(\widehat {DCE} = {45^o}.\)
Mặt khác \(\widehat {DCE} + \widehat {GCE} = \widehat {DCG}\) \( \Rightarrow \widehat {GCE} = \widehat {DCG} - \widehat {DCE} = {90^o} - {45^o} = {45^o}.\)
Xét \(\Delta DCE\) và \(\Delta GCE\) có:
\(EC\) chung
\(CD = CG\,\,(cmt)\)
\(\widehat {DCE} = \widehat {GCE} = {45^o}\)
\( \Rightarrow \Delta DCE = \Delta GCE\,\,(c.g.c)\)
\( \Rightarrow \widehat {CED} = \widehat {CEG}\) (hai cạnh tương ứng) (1)
Xét \(\Delta ADF\) và \(\Delta CDE\) có:
\(AD = CD\) (vì \(D\) là trung điểm \(AC\))
\(DF = DE\,\) (cách dựng)
\(\widehat {ADF} = \widehat {CDE}\) (hai góc đối đỉnh)
\( \Rightarrow \Delta ADF = \Delta CDE\,(c.g.c)\)
\( \Rightarrow \widehat {AFD} = \widehat {CED}\) (hai góc tương ứng) (2)
Mà \(\widehat {AFD}\) và \(\widehat {CED}\) ở vị trí so le trong nên \(AF//EC.\)
Vì \(AF//EC\) nên \(\widehat {GEC} = \widehat {EAF}\) (hai góc đồng vị) (3)
Từ (1), (2) và (3) suy ra \(\widehat {EAF} = \widehat {EFA}\), tam giác \(AEF\) cân tại \(E\) nên \(AE = EF\) (4)
Mà \(DE = DF\) (theo cách dựng) nên \(EF = 2DE\) (5)
Từ (4) và (5) ta có: \(AE = 2DE\).

