Câu hỏi:
3 năm trước
Cho tam giác \(ABC\) vuông tại \(A\)\(\left( {AB > AC} \right).\) Tia phân giác của góc \(B\) cắt \(AC\) ở \(D.\) Kẻ \(DH\) vuông góc với \(BC.\) Trên tia \(AC\) lấy \(E\) sao cho \(AE = AB.\) Đường thẳng vuông góc với \(AE\) tại \(E\) cắt tia \(DH\) tại \(K.\)
Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: d
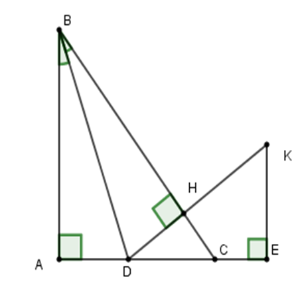
Xét hai tam giác vuông \(BAD\) và \(BHD\) có \(\widehat A = \widehat H = 90^\circ ;\,\widehat {ABD} = \widehat {HBD}\) (vì \(BD\) là tia phân giác góc \(B\)) và cạnh \(BD\) chung
\( \Rightarrow \Delta ABD = \Delta HBD\left( {ch - gn} \right)\) \( \Rightarrow BA = BH\) (hai cạnh tương ứng).
Hướng dẫn giải:
Chứng minh hai tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau

