Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông cân tại \(A\). Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) vuông góc với đường thẳng \(d.\) Khi đó tổng \(B{H^2} + C{K^2}\) bằng
Trả lời bởi giáo viên
Đáp án đúng: c
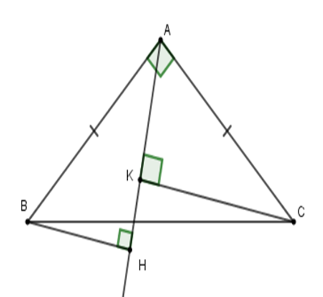
Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC\) (tính chất)
Lại có \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì \(\Delta ABH\) vuông tại \(H\) ) và \(\widehat {CAH} + \widehat {BAH} = 90^\circ \)
Nên \(\widehat {ABH} = \widehat {CAK}\) (cùng phụ với \(\widehat {BAH}\) )
\( \Rightarrow \Delta ABH = \Delta CAK\) (cạnh huyền-góc nhọn) suy ra \(BH = AK.\)
Do đó \(B{H^2} + C{K^2} = A{K^2} + C{K^2}\,\,\left( 1 \right)\)
Xét tam giác \(ACK\), theo định lý Pytago: \(A{K^2} + C{K^2} = A{C^2}\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(B{H^2} + C{K^2} = A{C^2}.\)
Hướng dẫn giải:
+ Chứng minh hai tam giác bằng nhau \(\Delta ABH = \Delta CAK\) suy ra các cạnh tương ứng bằng nhau
+ Sử dụng định lý Py-ta-go
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
