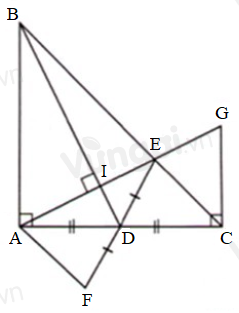
Cho tam giác \(ABC\) vuông cân tại \(A\) và \(D\) là trung điểm \(AC.\) Từ \(A\) kẻ đường vuông góc với \(BD,\) cắt \(BC\) tại \(E.\) Chọn đáp án đúng.

Từ \(C\) dựng đường thẳng vuông góc với \(AC\) cắt \(AE\) tại \(G\). Trên tia đối của tia \(DE\) lấy điểm \(F\) sao cho \(DE = DF\). Gọi \(I\) là giao điểm của \(AE\) và \(BD.\)

\(\Delta ABD\) vuông tại \(A\) nên \(\widehat {ABD} + \widehat {ADB} = {90^o}\)

\(\Delta AID\) vuông tại \(I\) nên \(\widehat {DAI} + \widehat {ADI} = {90^o}\)

Mà \(\widehat {ADB} = \widehat {ADI}\) nên \(\widehat {ABD} = \widehat {DAI}\) hay \(\widehat {ABD} = \widehat {CAG}\)

Xét \(\Delta ABD\) và \(\Delta CAG\) có:

\(\widehat {BAD} = \widehat {ACG} = {90^o}\)

\(AB = CA\) (vì \(\Delta ABC\) cân tại \(A\))

\(\widehat {ABD} = \widehat {CAG}\,\,(cmt)\)

\( \Rightarrow \Delta ABD = \Delta CAG\) (g.c.g).

\( \Rightarrow AD = CG\) (hai cạnh tương ứng).

Mà \(AD = CD\) (vì \(D\) là trung điểm của \(AC\)) nên \(CD = CG\)

\(\Delta ABC\) vuông cân tại \(A\) nên \(\widehat {ACB} = \dfrac{{{{180}^o} - \widehat A}}{2} = \dfrac{{{{180}^o} - {{90}^o}}}{2} = {45^o}\) hay \(\widehat {DCE} = {45^o}.\)

Mặt khác \(\widehat {DCE} + \widehat {GCE} = \widehat {DCG}\)  \( \Rightarrow \widehat {GCE} = \widehat {DCG} - \widehat {DCE} = {90^o} - {45^o} = {45^o}.\)

Xét \(\Delta DCE\) và \(\Delta GCE\) có:

\(EC\) chung

\(CD = CG\,\,(cmt)\)

\(\widehat {DCE} = \widehat {GCE} = {45^o}\)

\( \Rightarrow \Delta DCE = \Delta GCE\,\,(c.g.c)\)

\( \Rightarrow \widehat {CED} = \widehat {CEG}\) (hai cạnh tương ứng)    (1)

Xét \(\Delta ADF\) và \(\Delta CDE\) có:

\(AD = CD\) (vì \(D\) là trung điểm \(AC\))

\(DF = DE\,\) (cách dựng)

\(\widehat {ADF} = \widehat {CDE}\) (hai góc đối đỉnh)

\( \Rightarrow \Delta ADF = \Delta CDE\,(c.g.c)\)

\( \Rightarrow \widehat {AFD} = \widehat {CED}\) (hai góc tương ứng)       (2)

Mà \(\widehat {AFD}\) và \(\widehat {CED}\) ở vị trí so le trong nên \(AF//EC.\)

Vì \(AF//EC\) nên \(\widehat {GEC} = \widehat {EAF}\) (hai góc đồng vị)      (3)

Từ (1), (2) và (3) suy ra \(\widehat {EAF} = \widehat {EFA}\), tam giác \(AEF\) cân tại \(E\) nên \(AE = EF\)    (4)

Mà \(DE = DF\) (theo cách dựng) nên \(EF = 2DE\)    (5)

Từ (4) và (5) ta có: \(AE = 2DE\).