\(\Delta AIK\) là tam giác gì?
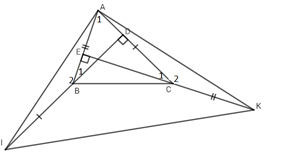
Ta có \(AI = AK\left( {cmt} \right) \Rightarrow \Delta AIK\) cân tại A (*).
\(\Delta ABI = \Delta KCA\left( {cmt} \right) \Rightarrow \widehat {AIB} = \widehat {CAK}\left( 3 \right)\)(2 góc tương ứng)
Xét \({\Delta _v}AID\) có: \(\widehat {AID} + \widehat {IAD} = {90^0}\left( 4 \right)\)(trong tam giác vuông 2 góc nhọn phụ nhau)
Từ \(\left( 3 \right)\left( 4 \right) \Rightarrow \widehat {IAD} + \widehat {CAK} = {90^0} \Rightarrow \Delta AIK\)vuông tại A (**)
Từ (*) và (**) \( \Rightarrow \Delta AIK\)vuông cân tại $A.$
Chọn câu đúng.
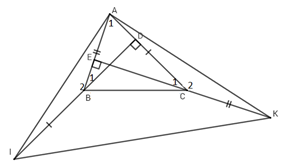
Xét \({\Delta _v}ABD\) có: \(\widehat {{A_1}} + \widehat {{B_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
Xét \({\Delta _v}AEC\) có: \(\widehat {{A_1}} + \widehat {{C_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
\( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\left( 1 \right)\).
Lại có: $\left\{ \begin{array}{l}\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\\\widehat {{C_1}} + \widehat {{C_2}} = {180^0}\end{array} \right.\left( 2 \right)$ (hai góc kề bù)
Từ \(\left( 1 \right);\;\left( 2 \right) \Rightarrow \widehat {{B_2}} = \widehat {{C_2}}\) .
Xét \(\Delta ABI\) và \(\Delta KCA\) có:
\(\left\{ \begin{array}{l}AB = CK\left( {gt} \right)\\\widehat {{B_2}} = \widehat {{C_2}}\left( {cmt} \right)\\BI = AC\left( {gt} \right)\end{array} \right. \Rightarrow \Delta ABI = \Delta KCA\left( {c - g - c} \right)\)\( \Rightarrow AI = AK\) (2 cạnh tương ứng)
Chọn câu đúng.

Xét \({\Delta _v}ABD\) có: \(\widehat {{A_1}} + \widehat {{B_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
Xét \({\Delta _v}AEC\) có: \(\widehat {{A_1}} + \widehat {{C_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
\( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\left( 1 \right)\).
Lại có: $\left\{ \begin{array}{l}\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\\\widehat {{C_1}} + \widehat {{C_2}} = {180^0}\end{array} \right.\left( 2 \right)$ (hai góc kề bù)
Từ \(\left( 1 \right);\;\left( 2 \right) \Rightarrow \widehat {{B_2}} = \widehat {{C_2}}\) .
Xét \(\Delta ABI\) và \(\Delta KCA\) có:
\(\left\{ \begin{array}{l}AB = CK\left( {gt} \right)\\\widehat {{B_2}} = \widehat {{C_2}}\left( {cmt} \right)\\BI = AC\left( {gt} \right)\end{array} \right. \Rightarrow \Delta ABI = \Delta KCA\left( {c - g - c} \right)\)\( \Rightarrow AI = AK\) (2 cạnh tương ứng)
Nếu \(DA = DB\) thì tam giác \(ABC\) là tam giác
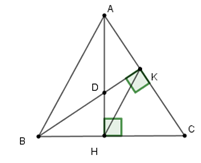
Nếu \(DA = DB\) thì tam giác \(DAB\) cân tại \(D\) suy ra \(\widehat {DBA} = \widehat {DAB}\,\left( 1 \right)\) (tính chất tam giác cân)
Xét tam giác vuông \(AHB\) có \(\widehat {ABH} = 90^\circ - \widehat {BAH}\,\left( 2 \right)\)
Xét tam giác vuông \(ABK\) có \(\widehat {BAK} = 90^\circ - \widehat {ABK}\,\left( 3 \right)\)
Từ (1); (2); (3) ta suy ra \(\widehat {ABH} = \widehat {BAK}\) hay \(\widehat {ABC} = \widehat {BAC}\) suy ra tam giác \(ABC\) cân tại \(C.\)
Biết \(\widehat {ACB} = 50^\circ \) , tính \(\widehat {HDK.}\)
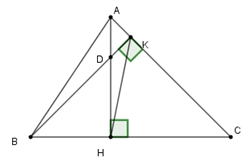
Xét tam giác \(CHK\) có \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} = 180^\circ \,\left( 1 \right)\) (định lý tổng ba góc trong tam giác)
Xét tam giác \(DHK\) có \(\widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \,\left( 2 \right)\) (định lý tổng ba góc trong tam giác)
Từ (1) và (2) suy ra \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} + \widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \, + 180^\circ \, = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {CHK} + \widehat {DHK} + \widehat {HDK} + \widehat {CKH} + \widehat {DKH} = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {DHC} + \widehat {HDK} + \widehat {DKC} = 360^\circ \) mà \(\widehat {CHD} = 90^\circ ;\,\widehat {DKC} = 90^\circ ;\,\widehat {HCK} = 50^\circ \)
Suy ra \(\widehat {HDK} = 360^\circ - 90^\circ - 90^\circ - 50^\circ = 130^\circ \).
Biết \(\widehat {ACB} = 50^\circ \) , tính \(\widehat {HDK.}\)

Xét tam giác \(CHK\) có \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} = 180^\circ \,\left( 1 \right)\) (định lý tổng ba góc trong tam giác)
Xét tam giác \(DHK\) có \(\widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \,\left( 2 \right)\) (định lý tổng ba góc trong tam giác)
Từ (1) và (2) suy ra \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} + \widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \, + 180^\circ \, = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {CHK} + \widehat {DHK} + \widehat {HDK} + \widehat {CKH} + \widehat {DKH} = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {DHC} + \widehat {HDK} + \widehat {DKC} = 360^\circ \) mà \(\widehat {CHD} = 90^\circ ;\,\widehat {DKC} = 90^\circ ;\,\widehat {HCK} = 50^\circ \)
Suy ra \(\widehat {HDK} = 360^\circ - 90^\circ - 90^\circ - 50^\circ = 130^\circ \).
Trực tâm của tam giác là giao của
Trực tâm của tam giác là giao của ba đường cao.
Cho tam giác \(ABC\) có \(AM\) là đường phân giác đồng thời cũng là đường cao, khi đó tam giác \(ABC\) là tam giác gì?
Vì tam giác \(ABC\) có \(AM\) là đường phân giác đồng thời cũng là đường cao nên là tam giác cân.
Cho \(\Delta ABC\) cân tại \(A,\) trung tuyến \(AM.\) Biết \(BC = 6cm, AM = 4cm.\) Tính độ dài các cạnh \(AB\) và \(AC.\)
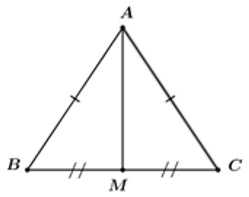
Vì \(\Delta ABC\) cân tại \(A\) (gt) mà \(AM\) là trung tuyến nên \(AM\) đồng thời cũng là đường cao của tam giác đó.
Vì \(AM\) là trung tuyến của \(\Delta ABC\) nên \(M\) là trung điểm của \(BC\)
\( \Rightarrow BM = \dfrac{{BC}}{2} = 6:2 = 3\,cm.\)
Xét \(\Delta AMB\) vuông tại \(M\) có: \(A{B^2} = A{M^2} + B{M^2}\) (định lý Py-ta-go)
\( \Rightarrow A{B^2} = {4^2} + {3^2} = 25 \Rightarrow AB = \sqrt {25} = 5\,cm.\)
\(\Delta ABC\) cân tại \(A\) nên \(AB = AC = 5\,cm.\)
Đường cao của tam giác đều cạnh \(4\) có bình phương độ dài đường cao là:
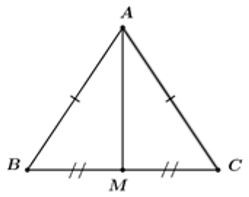
Xét tam giác \(ABC\) đều cạnh \(AB = BC = AC = 4\) có: \(AM\) là đường trung tuyến suy ra \(AM\) cũng là đường cao của tam giác \(ABC\) hay \(AM \bot BC\) tại \(M\).
Ta có: \(MB = MC = \dfrac{{BC}}{2} = \dfrac{4}{2} = 2\)
Xét tam giác \(AMC\) vuông tại \(M\), theo định lý Pytago ta có:
\(A{M^2} = A{C^2} - M{C^2} = {4^2} - {2^2}\)\( = 16 - 4 = 12\)
Vậy bình phương độ dài đường cao của tam giác đều cạnh \(4\) là \(12.\)
Gọi \(CH\) cắt \(AD\) tại \(K.\) Tính số đo góc \(CKA.\)

Gọi \(I\) là giao điểm của \(DH\) với \(AC.\)
Sử dụng kết quả câu trước ta có: \(DI \bot AC\).
Xét \(\Delta ADC\) có: \(AB\, \bot DC;\,DI \bot \,AC\) nên \(H\) là trực tâm của \(\Delta ADC.\)
Suy ra \(CK\) là đường cao thứ ba của \(\Delta ADC\) hay \(CK\, \bot AD\).
Do đó \(\widehat {CKA} = {90^o}.\)
Chọn câu đúng.

Gọi \(I\) là giao điểm của \(DH\) với \(AC.\)
\(\Delta ABC\) vuông cân tại \(B\) (gt) nên \(\widehat C = {45^o}\).
\(\Delta HBD\) có: \(\widehat {HBD} = {90^o};\,BH = BD\,\,(gt)\) nên \(\Delta HBD\) vuông cân tại \(B\) suy ra \(\widehat {BDH} = {45^o}\) hay \(\widehat {CDI} = {45^o}.\)
Xét \(\Delta DCI\) có: \(\widehat C = \widehat {CDI} = {45^o}\,\,(cmt)\) suy ra \(\widehat {DIC} = {180^o} - \left( {\widehat C + \widehat {CDI}} \right) = {180^o} - \left( {{{45}^o} + {{45}^o}} \right) = {90^o}.\)
Vậy \(DH\, \bot \,AC.\)
Chọn câu đúng.

Gọi \(I\) là giao điểm của \(DH\) với \(AC.\)
\(\Delta ABC\) vuông cân tại \(B\) (gt) nên \(\widehat C = {45^o}\).
\(\Delta HBD\) có: \(\widehat {HBD} = {90^o};\,BH = BD\,\,(gt)\) nên \(\Delta HBD\) vuông cân tại \(B\) suy ra \(\widehat {BDH} = {45^o}\) hay \(\widehat {CDI} = {45^o}.\)
Xét \(\Delta DCI\) có: \(\widehat C = \widehat {CDI} = {45^o}\,\,(cmt)\) suy ra \(\widehat {DIC} = {180^o} - \left( {\widehat C + \widehat {CDI}} \right) = {180^o} - \left( {{{45}^o} + {{45}^o}} \right) = {90^o}.\)
Vậy \(DH\, \bot \,AC.\)
Cho tam giác \(ABC\) vuông cân tại \(A.\) Trên cạnh \(AB\) lấy điểm \(D,\) trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AD.\) Kéo dài \(CD\) cắt \(BE\) tại \(I.\) Tính số đo góc \(\widehat {BIC}.\)
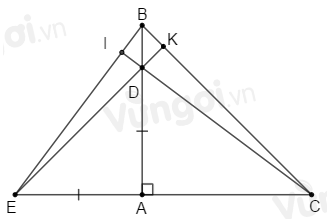
Gọi \(K\) là giao của \(ED\) và \(BC\).
\(\Delta ABC\) vuông cân tại \(A\) (gt) nên \(\widehat C = {45^o}\).
\(\Delta ADE\) có: \(\widehat {DAE} = {90^o};\,AD = AE\,\,(gt)\) nên \(\Delta ADE\) vuông cân tại \(A\) suy ra \(\widehat {AED} = {45^o}\) hay \(\widehat {CEK} = {45^o}.\)
Xét \(\Delta CEK\) có: \(\widehat C = \widehat {CEK} = {45^o}\,\,(cmt)\) suy ra \(\widehat {EKC} = {180^o} - \left( {\widehat C + \widehat {CEK}} \right) = {180^o} - \left( {{{45}^o} + {{45}^o}} \right) = {90^o}.\)
Vậy \(EK\, \bot \,BC.\)
Xét \(\Delta BCE\) có: \(BA\, \bot EC;\,EK \bot \,BC\) nên \(D\) là trực tâm của \(\Delta BCE\).
Suy ra \(CI\) là đường cao thứ ba của \(\Delta BCE\) hay \(CI\, \bot BE\).
Do đó \(\widehat {BIC} = {90^o}.\)
Cho \(\Delta ABC\) vuông tại \(A,\) trên cạnh \(AC\) lấy các điểm \(D,E\) sao cho \(\widehat {ABD} = \widehat {DBE} = \widehat {EBC}.\) Trên tia đối của tia \(DB\) lấy điểm \(F\) sao cho \(DF = BC.\) Tam giác \(CDF\) là tam giác gì?

Trên đoạn \(BF\) lấy điểm \(G\) sao cho \(BG = BC\) khi đó \(G\) nằm giữa \(D\) và \(F\).
Ta có: \(BG = BD + DG\)
\(DF = DG + GF\)
Mà \(BG = DF\) (cùng bằng \(BC\)) nên \(BD = GF.\)
\(\Delta BCG\) cân tại \(B\), \(\widehat {DBE} = \widehat {EBC}\) nên \(BE\) là phân giác đồng thời là đường cao của \(\Delta BCG\).
Gọi \(H\) là giao của \(BE\) và \(GC\) nên \(BH\, \bot \,GC.\)
\(\Delta BHG\) vuông tại \(H\) nên \(\widehat {HGB} + \widehat {GBH} = {90^o} \Rightarrow \widehat {CGB} = {90^o} - \dfrac{1}{3}\widehat {ABC}\)
\(\Delta ABD\) vuông tại \(A\) nên \(\widehat {ABD} + \widehat {ADB} = {90^o} \Rightarrow \widehat {ADB} = {90^o} - \dfrac{1}{3}\widehat {ABC}\)
Mà \(\widehat {CDG} = \widehat {ADB}\) (hai góc đối đỉnh) nên \(\widehat {CDG} = {90^o} - \dfrac{1}{3}\widehat {ABC}\)
Do đó \(\widehat {CGB} = \widehat {CDG} = {90^o} - \dfrac{1}{3}\widehat {ABC}\) nên \(\Delta CDG\) cân tại \(C\) suy ra \(CD = CG\) (tính chất tam giác cân)
\(\widehat {CDB}\) là góc ngoài tại đỉnh \(D\) của \(\Delta CDG\) nên \(\widehat {CDB} = \widehat {DCG} + \widehat {CGD}\) (1)
\(\widehat {CGF}\) là góc ngoài tại đỉnh \(G\) của \(\Delta CDG\) nên \(\widehat {CGF} = \widehat {DCG} + \widehat {CDG}\) (2)
Mà \(\widehat {CDG} = \widehat {CGD}\) (vì \(\Delta CDG\) cân tại \(C\)) (3)
Từ (1), (2), (3) suy ra \(\widehat {CDB} = \widehat {CGF}\)
Xét \(\Delta CDB\) và \(\Delta CGF\) có:
\(CD = CG\,\,\,(cmt)\)
\(BD = FG\,\,(cmt)\)
\(\widehat {CDB} = \widehat {CGF}\,\,(cmt)\)
\( \Rightarrow \Delta CDB = \Delta CGF\,\,(c.g.c)\)
\( \Rightarrow CB = CF\) (hai cạnh tương ứng)
\( \Rightarrow CF = DF\) (vì cùng bằng \(BC)\)
Vậy \(\Delta CDF\) cân tại \(F.\)
Nếu \(DA = DB\) và \(\widehat {BAC} = {60^0}\). Chọn câu đúng nhất.

Nếu \(DA = DB\) thì tam giác \(DAB\) cân tại \(D\) suy ra \(\widehat {DBA} = \widehat {DAB}\,\left( 1 \right)\) (tính chất tam giác cân)
Xét tam giác vuông \(AHB\) có: \(\widehat {ABH} = 90^\circ - \widehat {BAH}\,\left( 2 \right)\)
Xét tam giác vuông \(ABK\) có: \(\widehat {BAK} = 90^\circ - \widehat {ABK}\,\left( 3 \right)\)
Từ (1); (2); (3) ta suy ra: \(\widehat {ABH} = \widehat {BAK}\) hay \(\widehat {ABC} = \widehat {BAC}\) suy ra tam giác \(ABC\) cân tại \(C.\)
Lại có: \(\widehat {BAC} = {60^0}\,\,(gt)\) nên \(\Delta ABC\) là tam giác đều.
Biết \(\widehat {ACB} = 44^\circ \), tính \(\widehat {HDK.}\)

Xét tam giác \(CHK\) có: \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} = 180^\circ \,\left( 1 \right)\) (định lý tổng ba góc của một tam giác)
Xét tam giác \(DHK\) có: \(\widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \,\left( 2 \right)\) (định lý tổng ba góc của một tam giác)
Từ (1) và (2) suy ra: \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} + \widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \, + 180^\circ \, = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {CHK} + \widehat {DHK} + \widehat {HDK} + \widehat {CKH} + \widehat {DKH} = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {DHC} + \widehat {HDK} + \widehat {DKC} = 360^\circ \) mà \(\widehat {DHC} = 90^\circ ;\,\widehat {DKC} = 90^\circ ;\,\widehat {HCK} = 44^\circ \)
Suy ra \(\widehat {HDK} = 360^\circ - 90^\circ - 90^\circ - 44^\circ = 136^\circ \).
Biết \(\widehat {ACB} = 44^\circ \), tính \(\widehat {HDK.}\)

Xét tam giác \(CHK\) có: \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} = 180^\circ \,\left( 1 \right)\) (định lý tổng ba góc của một tam giác)
Xét tam giác \(DHK\) có: \(\widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \,\left( 2 \right)\) (định lý tổng ba góc của một tam giác)
Từ (1) và (2) suy ra: \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} + \widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \, + 180^\circ \, = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {CHK} + \widehat {DHK} + \widehat {HDK} + \widehat {CKH} + \widehat {DKH} = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {DHC} + \widehat {HDK} + \widehat {DKC} = 360^\circ \) mà \(\widehat {DHC} = 90^\circ ;\,\widehat {DKC} = 90^\circ ;\,\widehat {HCK} = 44^\circ \)
Suy ra \(\widehat {HDK} = 360^\circ - 90^\circ - 90^\circ - 44^\circ = 136^\circ \).
Cho \(\Delta ABC\) có góc A nhọn. Kẻ hai đường cao \(BK\) và \(CH.\) Trên tia đối của tia \(BK\) lấy điểm \(E\) sao cho \(BE = AC.\) Trên tia đối của tia \(CH\) lấy điểm \(F\) sao cho \(CF = AB.\) Chọn câu đúng.

\(\widehat {ABE}\) là góc ngoài tại đỉnh \(B\) của \(\Delta ABK\) nên \(\widehat {ABE} = \widehat {BAK} + \widehat {AKB} = \widehat {BAC} + {90^o}\)
\(\widehat {FCA}\) là góc ngoài tại đỉnh \(C\) của \(\Delta ACH\) nên \(\widehat {FCA} = \widehat {CAH} + \widehat {AHC} = \widehat {BAC} + {90^o}\)
\( \Rightarrow \widehat {ABE} = \widehat {FCA}\, = \widehat {ABC} + {90^o}\).
Xét \(\Delta ABE\) và \(\Delta FCA\) có:
\(\begin{array}{l}AB = FC\,\,(gt)\\EB = AC\,(gt)\\\widehat {ABE} = \widehat {FCA}\,(cmt)\end{array}\)
\( \Rightarrow \Delta ABE = \Delta FCA\,(c.g.c)\).
\( \Rightarrow \widehat {BAE} = \widehat {CFA}\) (hai góc tương ứng).
\( \Rightarrow AE = FA\) (hai cạnh tương ứng).
\(\Delta AHF\) vuông tại \(H\) nên \(\widehat {HAF} + \widehat {HFA} = {90^o}\) hay \(\widehat {HAF} + \widehat {CFA} = {90^o}\)
Mà \(\widehat {BAE} = \widehat {CFA}\,\,(cmt)\) suy ra \(\widehat {HAF} + \widehat {BAE} = {90^o}\) hay \(\widehat {EAF} = {90^o}.\)
\(\Delta AEF\) có: \(AE = FA\,(cmt)\), \(\widehat {EAF} = {90^o}\,(cmt)\) nên \(\Delta AEF\) vuông cân tại \(A.\)
Biết \(AH = 6cm,BC = 8cm.\) Tính \(IK.\)
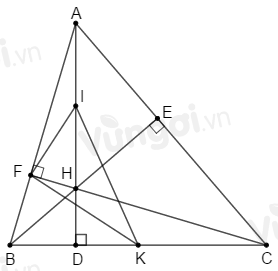
Sử dụng kết quả câu trước ta có: \(\widehat {IFK} = {90^o}\) hay \(\Delta IFK\) vuông tại \(F\) và \(FI = \dfrac{1}{2}AH;\,FK = \dfrac{1}{2}BC.\)
Ta có: \(FI = \dfrac{1}{2}AH = \dfrac{1}{2}.6 = 3\,(cm);\,FK = \dfrac{1}{2}BC = \dfrac{1}{2}.8 = 4\,(cm).\)
Áp dụng định lí Pytago vào tam giác vuông \(IFK\) ta có:
\(\begin{array}{l}I{K^2} = F{I^2} + F{K^2} = {3^2} + {4^2} = 25\\ \Rightarrow IK = \sqrt {25} = 5\,\left( {cm} \right).\end{array}\).

