Tính số đo góc \(\widehat {IFK}.\)
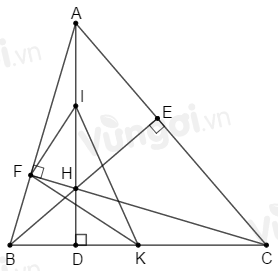
\(H\) là giao của hai đường cao \(BE;\,CF\) nên \(H\) là trực tâm của \(\Delta ABC.\)
Gọi \(D\) là giao của \(AH\) và \(BC\) nên \(AD\, \bot BC.\)
Xét \(\Delta AFH\) vuông tại \(F\), đường trung tuyến \(FI\) nên \(FI = IA = \dfrac{1}{2}AH\) (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).
Do đó \(\Delta FAI\) cân tại \(I\) suy ra \(\widehat {IFA} = \widehat {IAF}\) (1)
Xét \(\Delta BFC\) vuông tại \(F\), đường trung tuyến \(FK\) nên \(FK = BK = \dfrac{1}{2}BC\) (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).
Do đó \(\Delta FBK\) cân tại \(K\) suy ra \(\widehat {KFB} = \widehat {KBF}\) (2)
Xét \(\Delta ABD\) vuông tại \(D\) nên \(\widehat {DAB} + \widehat {DBA} = {90^o}.\)
Từ (1) và (2) suy ra \(\widehat {IFA} + \widehat {KFB} = \widehat {IAF} + \widehat {KBF} = \widehat {DAB} + \widehat {DBA} = {90^o}.\)
Ta có: \(\widehat {IFA} + \widehat {IFK} + \widehat {KFB} = {180^o}\)
\( \Rightarrow \widehat {IFK} = {180^o} - \left( {\widehat {IFA} + \widehat {KFB}} \right) = {180^o} - {90^o} = {90^o}\).
Tính số đo góc \(\widehat {IFK}.\)

\(H\) là giao của hai đường cao \(BE;\,CF\) nên \(H\) là trực tâm của \(\Delta ABC.\)
Gọi \(D\) là giao của \(AH\) và \(BC\) nên \(AD\, \bot BC.\)
Xét \(\Delta AFH\) vuông tại \(F\), đường trung tuyến \(FI\) nên \(FI = IA = \dfrac{1}{2}AH\) (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).
Do đó \(\Delta FAI\) cân tại \(I\) suy ra \(\widehat {IFA} = \widehat {IAF}\) (1)
Xét \(\Delta BFC\) vuông tại \(F\), đường trung tuyến \(FK\) nên \(FK = BK = \dfrac{1}{2}BC\) (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).
Do đó \(\Delta FBK\) cân tại \(K\) suy ra \(\widehat {KFB} = \widehat {KBF}\) (2)
Xét \(\Delta ABD\) vuông tại \(D\) nên \(\widehat {DAB} + \widehat {DBA} = {90^o}.\)
Từ (1) và (2) suy ra \(\widehat {IFA} + \widehat {KFB} = \widehat {IAF} + \widehat {KBF} = \widehat {DAB} + \widehat {DBA} = {90^o}.\)
Ta có: \(\widehat {IFA} + \widehat {IFK} + \widehat {KFB} = {180^o}\)
\( \Rightarrow \widehat {IFK} = {180^o} - \left( {\widehat {IFA} + \widehat {KFB}} \right) = {180^o} - {90^o} = {90^o}\).
Tam giác \(IEF\) là tam giác gì?
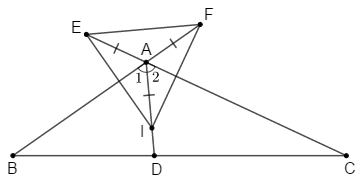
Sử dụng kết quả câu trước ta có: \(AB\) là đường trung trực của \(IE\), \(AC\) là đường trung trực của \(IF.\)
Vì \(E\) nằm trên đường trung trực của \(IF\) nên \(EF = EI\) (tính chất đường trung trực) (1)
Vì \(F\) nằm trên đường trung trực của \(IE\) nên \(EF = FI\) (tính chất đường trung trực) (2)
Từ (1) và (2) suy ra:\(EF = EI = FI\) do đó \(\Delta IEF\) là tam giác đều.
Chọn câu sai.
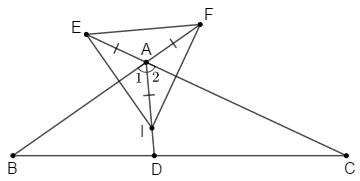
\(\Delta ABC\) có: \(\widehat B + \widehat C = {60^o}\,(gt)\) nên \(\widehat {BAC} = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - {60^o} = {120^o}\) (tổng ba góc của một tam giác)
Mà \(AD\) là tia phân giác \(\widehat {BAC}\) nên \(\widehat {{A_1}} = \widehat {{A_2}} = \dfrac{{{{120}^o}}}{2} = {60^o}\).
\(\widehat {EAB}\) là góc ngoài tại đỉnh \(A\) của \(\Delta ABC\) nên \(\widehat {EAB} = \widehat B + \widehat C = {60^o}.\)
Do đó \(\widehat {EAB} = \widehat {{A_1}} = {60^o}.\)
\(\Delta EAI\) cân tại \(A\) (vì \(AE = AD\,(gt)\)) mà \(AB\) là phân giác nên \(AB\) là đường trung trực của \(IE.\)
Ta có:\(\widehat {FAC} = \widehat {EAB}\) (hai góc đối đỉnh) nên \(\widehat {FAC} = {60^o}.\)
Do đó \(AC\) là phân giác của \(\widehat {FAI}\).
\(\Delta FAI\) cân tại \(I\) (vì \(AI = \,AF\,(gt)\)) mà \(AC\) là phân giác nên \(AC\) là đường trung trực của \(IF.\)
Vậy cả A, B, C đều đúng.
Chọn câu sai.

\(\Delta ABC\) có: \(\widehat B + \widehat C = {60^o}\,(gt)\) nên \(\widehat {BAC} = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - {60^o} = {120^o}\) (tổng ba góc của một tam giác)
Mà \(AD\) là tia phân giác \(\widehat {BAC}\) nên \(\widehat {{A_1}} = \widehat {{A_2}} = \dfrac{{{{120}^o}}}{2} = {60^o}\).
\(\widehat {EAB}\) là góc ngoài tại đỉnh \(A\) của \(\Delta ABC\) nên \(\widehat {EAB} = \widehat B + \widehat C = {60^o}.\)
Do đó \(\widehat {EAB} = \widehat {{A_1}} = {60^o}.\)
\(\Delta EAI\) cân tại \(A\) (vì \(AE = AD\,(gt)\)) mà \(AB\) là phân giác nên \(AB\) là đường trung trực của \(IE.\)
Ta có:\(\widehat {FAC} = \widehat {EAB}\) (hai góc đối đỉnh) nên \(\widehat {FAC} = {60^o}.\)
Do đó \(AC\) là phân giác của \(\widehat {FAI}\).
\(\Delta FAI\) cân tại \(I\) (vì \(AI = \,AF\,(gt)\)) mà \(AC\) là phân giác nên \(AC\) là đường trung trực của \(IF.\)
Vậy cả A, B, C đều đúng.
Tam giác \(IEF\) là tam giác gì?

Sử dụng kết quả câu trước ta có: \(AB\) là đường trung trực của \(IE\), \(AC\) là đường trung trực của \(IF.\)
Vì \(E\) nằm trên đường trung trực của \(IF\) nên \(EF = EI\) (tính chất đường trung trực) (1)
Vì \(F\) nằm trên đường trung trực của \(IE\) nên \(EF = FI\) (tính chất đường trung trực) (2)
Từ (1) và (2) suy ra:\(EF = EI = FI\) do đó \(\Delta IEF\) là tam giác đều.
Chọn câu đúng nhất.

\(\Delta ABC\) có: \(\widehat B + \widehat C = {60^o}\,(gt)\) nên \(\widehat {BAC} = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - {60^o} = {120^o}\) (tổng ba góc của một tam giác)
Mà \(AD\) là tia phân giác \(\widehat {BAC}\) nên \(\widehat {{A_1}} = \widehat {{A_2}} = \dfrac{{{{120}^o}}}{2} = {60^o}\).
\(\widehat {EAB}\) là góc ngoài tại đỉnh \(A\) của \(\Delta ABC\) nên \(\widehat {EAB} = \widehat B + \widehat C = {60^o}.\)
Do đó \(\widehat {EAB} = \widehat {{A_1}} = {60^o}.\)
\(\Delta EAI\) cân tại \(A\) (vì \(AE = AD\,(gt)\)) mà \(AB\) là phân giác nên \(AB\) là đường trung trực của \(IE.\)
Ta có:\(\widehat {FAC} = \widehat {EAB}\) (hai góc đối đỉnh) nên \(\widehat {FAC} = {60^o}.\)
Do đó \(AC\) là phân giác của \(\widehat {FAI}\).
\(\Delta FAI\) cân tại \(A\) (vì \(AI = \,AF\,(gt)\)) mà \(AC\) là phân giác nên \(AC\) là đường trung trực của \(IF.\)
Vậy cả A, B, C đều đúng.
Chọn câu đúng nhất.

\(\Delta ABC\) có: \(\widehat B + \widehat C = {60^o}\,(gt)\) nên \(\widehat {BAC} = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - {60^o} = {120^o}\) (tổng ba góc của một tam giác)
Mà \(AD\) là tia phân giác \(\widehat {BAC}\) nên \(\widehat {{A_1}} = \widehat {{A_2}} = \dfrac{{{{120}^o}}}{2} = {60^o}\).
\(\widehat {EAB}\) là góc ngoài tại đỉnh \(A\) của \(\Delta ABC\) nên \(\widehat {EAB} = \widehat B + \widehat C = {60^o}.\)
Do đó \(\widehat {EAB} = \widehat {{A_1}} = {60^o}.\)
\(\Delta EAI\) cân tại \(A\) (vì \(AE = AD\,(gt)\)) mà \(AB\) là phân giác nên \(AB\) là đường trung trực của \(IE.\)
Ta có:\(\widehat {FAC} = \widehat {EAB}\) (hai góc đối đỉnh) nên \(\widehat {FAC} = {60^o}.\)
Do đó \(AC\) là phân giác của \(\widehat {FAI}\).
\(\Delta FAI\) cân tại \(A\) (vì \(AI = \,AF\,(gt)\)) mà \(AC\) là phân giác nên \(AC\) là đường trung trực của \(IF.\)
Vậy cả A, B, C đều đúng.
Chọn câu đúng.
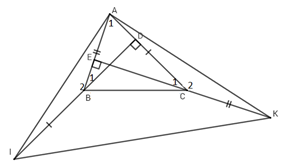
Xét \({\Delta _v}ABD\) có: \(\widehat {{A_1}} + \widehat {{B_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
Xét \({\Delta _v}AEC\) có: \(\widehat {{A_1}} + \widehat {{C_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
\( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\left( 1 \right)\).
Lại có: $\left\{ \begin{array}{l}\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\\\widehat {{C_1}} + \widehat {{C_2}} = {180^0}\end{array} \right.\left( 2 \right)$ (hai góc kề bù)
Từ \(\left( 1 \right);\;\left( 2 \right) \Rightarrow \widehat {{B_2}} = \widehat {{C_2}}\) .
Xét \(\Delta ABI\) và \(\Delta KCA\) có:
\(\left\{ \begin{array}{l}AB = CK\left( {gt} \right)\\\widehat {{B_2}} = \widehat {{C_2}}\left( {cmt} \right)\\BI = AC\left( {gt} \right)\end{array} \right. \Rightarrow \Delta ABI = \Delta KCA\left( {c - g - c} \right)\)\( \Rightarrow AI = AK\) (2 cạnh tương ứng)
Biết \(\widehat {ACB} = 50^\circ \) , tính \(\widehat {HDK.}\)
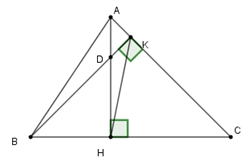
Xét tam giác \(CHK\) có \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} = 180^\circ \,\left( 1 \right)\) (định lý tổng ba góc trong tam giác)
Xét tam giác \(DHK\) có \(\widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \,\left( 2 \right)\) (định lý tổng ba góc trong tam giác)
Từ (1) và (2) suy ra \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} + \widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \, + 180^\circ \, = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {CHK} + \widehat {DHK} + \widehat {HDK} + \widehat {CKH} + \widehat {DKH} = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {DHC} + \widehat {HDK} + \widehat {DKC} = 360^\circ \) mà \(\widehat {CHD} = 90^\circ ;\,\widehat {DKC} = 90^\circ ;\,\widehat {HCK} = 50^\circ \)
Suy ra \(\widehat {HDK} = 360^\circ - 90^\circ - 90^\circ - 50^\circ = 130^\circ \).
Cho \(\Delta ABC\), hai đường cao $AM$ và $BN$ cắt nhau tại $H.$ Em hãy chọn phát biểu đúng:
Vì hai đường cao $AM$ và $BN$ cắt nhau tại $H$ nên $CH$ là đường cao của \(\Delta ABC\) và \(H\) là trực tâm tam giác \(ABC\) nên A, B, D sai, C đúng.
Cho tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến khi đó
Vì tam giác \(ABC\) cân tại \(A\) có \(AM\) là đường trung tuyến nên \(AM\) cũng là đường cao, đường trung trực và đường phân giác của tam giác \(ABC.\)
Cho \(\Delta ABC\) cân tại $A,$ trung tuyến $AM.$ Biết $BC = 24cm,AM = 5cm.$ Tính độ dài các cạnh $AB$ và $AC.$
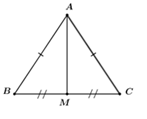
Vì \(\Delta ABC\) cân tại $A$ (gt) mà $AM$ là trung tuyến nên $AM$ cũng là đường cao của tam giác đó.
Vì $AM$ là trung tuyến của \(\Delta ABC\) nên $M$ là trung điểm của $BC$
\( \Rightarrow BM = \dfrac{{BC}}{2} = 24:2 = 12cm.\)
Xét \(\Delta AMB\) vuông tại \(M\) có: \(A{B^2} = A{M^2} + B{M^2}\) (định lý py-ta-go)
\( \Rightarrow A{B^2} = {12^2} + {5^2} = 169 \Rightarrow AB = \sqrt {169} = 13cm.\)
Vậy $AB = AC = 13cm.$
Đường cao của tam giác đều cạnh \(a\) có bình phương độ dài là
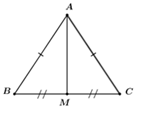
Xét tam giác \(ABC\) đều cạnh \(AB = BC = AC = a\) có \(AM\) là đường trung tuyến suy ra \(AM\) cũng là đường cao của tam giác \(ABC\) hay \(AM \bot BC\) tại \(M\).
Ta có \(MB = MC = \dfrac{{BC}}{2} = \dfrac{a}{2}\)
Xét tam giác $AMC$ vuông tại \(M\), theo định lý Pytago ta có
\(A{M^2} = A{C^2} - M{C^2} = {a^2} - {\left( {\dfrac{a}{2}} \right)^2}\)\( = {a^2} - \dfrac{{{a^2}}}{4} = \dfrac{{3{a^2}}}{4}\)
Vậy bình phương độ dài đường cao của tam giác đều cạnh \(a\) là \(\dfrac{{3{a^2}}}{4}.\)
Cho \(\Delta ABC\) nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho \(BI = AC\). Trên tia đối của tia CE lấy điểm K sao cho\(CK = AB.\)
Chọn câu đúng.

Xét \({\Delta _v}ABD\) có: \(\widehat {{A_1}} + \widehat {{B_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
Xét \({\Delta _v}AEC\) có: \(\widehat {{A_1}} + \widehat {{C_1}} = {90^0}\) (trong tam giác vuông 2 góc nhọn phụ nhau)
\( \Rightarrow \widehat {{B_1}} = \widehat {{C_1}}\left( 1 \right)\).
Lại có: $\left\{ \begin{array}{l}\widehat {{B_1}} + \widehat {{B_2}} = {180^0}\\\widehat {{C_1}} + \widehat {{C_2}} = {180^0}\end{array} \right.\left( 2 \right)$ (hai góc kề bù)
Từ \(\left( 1 \right);\;\left( 2 \right) \Rightarrow \widehat {{B_2}} = \widehat {{C_2}}\) .
Xét \(\Delta ABI\) và \(\Delta KCA\) có:
\(\left\{ \begin{array}{l}AB = CK\left( {gt} \right)\\\widehat {{B_2}} = \widehat {{C_2}}\left( {cmt} \right)\\BI = AC\left( {gt} \right)\end{array} \right. \Rightarrow \Delta ABI = \Delta KCA\left( {c - g - c} \right)\)\( \Rightarrow AI = AK\) (2 cạnh tương ứng)
Cho \(\Delta ABC\) nhọn, hai đường cao BD và CE. Trên tia đối của tia BD lấy điểm I sao cho \(BI = AC\). Trên tia đối của tia CE lấy điểm K sao cho\(CK = AB.\)
\(\Delta AIK\) là tam giác gì?
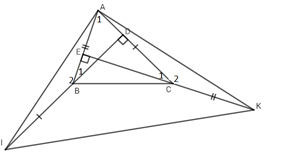
Ta có \(AI = AK\left( {cmt} \right) \Rightarrow \Delta AIK\) cân tại A (*).
\(\Delta ABI = \Delta KCA\left( {cmt} \right) \Rightarrow \widehat {AIB} = \widehat {CAK}\left( 3 \right)\)(2 góc tương ứng)
Xét \({\Delta _v}AID\) có: \(\widehat {AID} + \widehat {IAD} = {90^0}\left( 4 \right)\)(trong tam giác vuông 2 góc nhọn phụ nhau)
Từ \(\left( 3 \right)\left( 4 \right) \Rightarrow \widehat {IAD} + \widehat {CAK} = {90^0} \Rightarrow \Delta AIK\)vuông tại A (**)
Từ (*) và (**) \( \Rightarrow \Delta AIK\)vuông cân tại $A.$
Cho đoạn thẳng $AB$ và điểm $M$ nằm giữa $A$ và $B$$\;\left( {MA < MB} \right).$ Vẽ tia $Mx$ vuông góc với $AB,$ trên đó lấy hai điểm $C$ và $D$ sao cho $MA = MC,MD = MB.$ Tia $AC$ cắt $BD$ ở $E.$ Tính số đo \(\widehat {AEB}\)
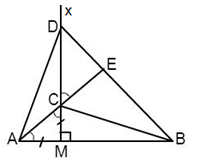
Vì $Mx \bot AB \Rightarrow \widehat {AMx} = {90^0}$
Xét $\Delta AMC$ có $\left\{ \begin{array}{l}\widehat {AMC} = {90^0}\left( {cmt} \right)\\MA = MC\left( {gt} \right)\end{array} \right. $ $\Rightarrow \widehat {MAC} = \widehat {MCA} = {45^0}$ (tính chất tam giác vuông cân)
Do đó \(\widehat {DCE} = \widehat {MCA} = {45^0}\) (đối đỉnh)
Xét $\Delta BMD$ có: $\left\{ \begin{array}{l}\widehat {BMD} = {90^0}\left( {cmt} \right)\\MB = MD\left( {gt} \right)\end{array} \right. $ $\Rightarrow \widehat {MBD} = \widehat {MDB} = {45^0}$(tính chất tam giác vuông cân)
Xét $\Delta CDE$ có: \(\widehat {CDE} = \widehat {DCE} = {45^0} \) \(\Rightarrow \widehat {CDE} + \widehat {DCE} = {90^0} \Rightarrow \widehat {DEC} = {90^0}.\)
Lại có: \(\widehat {DEC} + \widehat {AEB} = {180^0}\) (kề bù) \( \Rightarrow \widehat {AEB} = {180^0} - \widehat {DEC} = {180^0} - {90^0} = {90^0}\) .
Cho \(\Delta ABC\) cân tại $A,$ hai đường cao $BD$ và $CE$ cắt nhau tại $I.$ Tia $AI$ cắt $BC$ tại $M.$ Khi đó \(\Delta MED\)là tam giác gì?
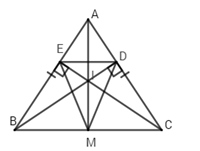
Xét \(\Delta ABC\) có $BD$ và $CE$ là hai đường cao cắt nhau tại $I$ suy ra $AI$ là đường cao của tam giác đó.
Mà $AI$ cắt $BC$ tại $M$ nên \(AM \bot BC\).
Vì \(\Delta ABC\) cân tại $A$ (gt) nên $AM$ là đường cao cũng chính là đường trung tuyến của tam giác đó. (tính chất của tam giác cân).
\( \Rightarrow BM = MC\) (tính chất đường trung tuyến)
Vì \(\left\{ \begin{array}{l}CE \bot AB\\BD \bot AC\end{array} \right. \Rightarrow \widehat {BEC} = \widehat {BDC} = {90^0}\).
Xét \({\Delta _v}BEC\) có $M$ là trung điểm của $BC$ nên suy ra $EM$ là trung tuyến của \({\Delta _v}BEC\)
\( \Rightarrow EM = \dfrac{{BC}}{2}\left( 1 \right)\) (tính chất trung tuyến của tam giác vuông)
Xét \({\Delta _v}BDC\) có $M$ là trung điểm của $BC$ nên suy ra $DM$ là trung tuyến của \({\Delta _v}BDC\)
\( \Rightarrow DM = \dfrac{{BC}}{2}\left( 2 \right)\) (tính chất trung tuyến của tam giác vuông)
Từ \(\left( 1 \right)\left( 2 \right) \Rightarrow EM = DM \Rightarrow \Delta EMD\) cân tại $M$ (dấu hiệu nhận biết tam giác cân).
Cho tam giác nhọn \(ABC\) có hai đường cao \(AH\) và \(BK\) cắt nhau tại \(D.\)
Biết \(\widehat {ACB} = 50^\circ \) , tính \(\widehat {HDK.}\)

Xét tam giác \(CHK\) có \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} = 180^\circ \,\left( 1 \right)\) (định lý tổng ba góc trong tam giác)
Xét tam giác \(DHK\) có \(\widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \,\left( 2 \right)\) (định lý tổng ba góc trong tam giác)
Từ (1) và (2) suy ra \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} + \widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \, + 180^\circ \, = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {CHK} + \widehat {DHK} + \widehat {HDK} + \widehat {CKH} + \widehat {DKH} = 360^\circ \)
\( \Rightarrow \widehat {HCK} + \widehat {DHC} + \widehat {HDK} + \widehat {DKC} = 360^\circ \) mà \(\widehat {CHD} = 90^\circ ;\,\widehat {DKC} = 90^\circ ;\,\widehat {HCK} = 50^\circ \)
Suy ra \(\widehat {HDK} = 360^\circ - 90^\circ - 90^\circ - 50^\circ = 130^\circ \).
Cho tam giác nhọn \(ABC\) có hai đường cao \(AH\) và \(BK\) cắt nhau tại \(D.\)
Nếu \(DA = DB\) thì tam giác \(ABC\) là tam giác
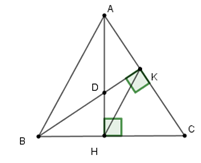
Nếu \(DA = DB\) thì tam giác \(DAB\) cân tại \(D\) suy ra \(\widehat {DBA} = \widehat {DAB}\,\left( 1 \right)\) (tính chất tam giác cân)
Xét tam giác vuông \(AHB\) có \(\widehat {ABH} = 90^\circ - \widehat {BAH}\,\left( 2 \right)\)
Xét tam giác vuông \(ABK\) có \(\widehat {BAK} = 90^\circ - \widehat {ABK}\,\left( 3 \right)\)
Từ (1); (2); (3) ta suy ra \(\widehat {ABH} = \widehat {BAK}\) hay \(\widehat {ABC} = \widehat {BAC}\) suy ra tam giác \(ABC\) cân tại \(C.\)

