Tính số đo góc \(\widehat {IFK}.\)

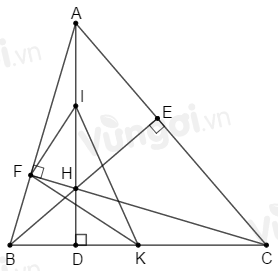
\(H\) là giao của hai đường cao \(BE;\,CF\) nên \(H\) là trực tâm của \(\Delta ABC.\)

Gọi \(D\) là giao của \(AH\) và \(BC\) nên \(AD\, \bot BC.\)

Xét \(\Delta AFH\) vuông tại \(F\), đường trung tuyến \(FI\) nên \(FI = IA = \dfrac{1}{2}AH\) (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).

Do đó \(\Delta FAI\) cân tại \(I\) suy ra \(\widehat {IFA} = \widehat {IAF}\)     (1)

Xét \(\Delta BFC\) vuông tại \(F\), đường trung tuyến \(FK\) nên \(FK = BK = \dfrac{1}{2}BC\) (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền).

Do đó \(\Delta FBK\) cân tại \(K\) suy ra \(\widehat {KFB} = \widehat {KBF}\)     (2)

Xét \(\Delta ABD\) vuông tại \(D\) nên \(\widehat {DAB} + \widehat {DBA} = {90^o}.\)

Từ (1) và (2) suy ra \(\widehat {IFA} + \widehat {KFB} = \widehat {IAF} + \widehat {KBF} = \widehat {DAB} + \widehat {DBA} = {90^o}.\)

Ta có: \(\widehat {IFA} + \widehat {IFK} + \widehat {KFB} = {180^o}\)

\( \Rightarrow \widehat {IFK} = {180^o} - \left( {\widehat {IFA} + \widehat {KFB}} \right) = {180^o} - {90^o} = {90^o}\).