Chọn câu đúng nhất.

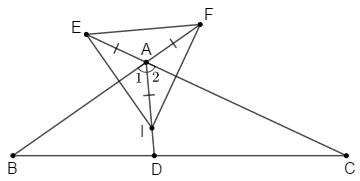
$\Delta ABC$ có: $\widehat B + \widehat C = {60^o}\,(gt)$ nên $\widehat {BAC} = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - {60^o} = {120^o}$ (tổng ba góc của một tam giác)

Mà $AD$ là tia phân giác $\widehat {BAC}$ nên $\widehat {{A_1}} = \widehat {{A_2}} = \dfrac{{{{120}^o}}}{2} = {60^o}$.

$\widehat {EAB}$ là góc ngoài tại đỉnh $A$ của $\Delta ABC$ nên $\widehat {EAB} = \widehat B + \widehat C = {60^o}.$

Do đó $\widehat {EAB} = \widehat {{A_1}} = {60^o}.$

$\Delta EAI$ cân tại $A$ (vì $AE = AD\,(gt)$) mà $AB$ là phân giác nên $AB$ là đường trung trực của $IE.$

Ta có:$\widehat {FAC} = \widehat {EAB}$ (hai góc đối đỉnh) nên $\widehat {FAC} = {60^o}.$

Do đó $AC$ là phân giác của $\widehat {FAI}$.

$\Delta FAI$ cân tại $A$ (vì $AI = \,AF\,(gt)$) mà $AC$ là phân giác nên $AC$ là đường trung trực của $IF.$

Vậy cả A, B, C đều đúng.