Cho tam giác nhọn \(ABC\) có hai đường cao \(AH\) và \(BK\) cắt nhau tại \(D.\)

Biết \(\widehat {ACB} = 50^\circ \) , tính \(\widehat {HDK.}\)

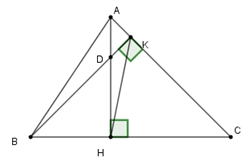
Xét tam giác \(CHK\) có \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} = 180^\circ \,\left( 1 \right)\) (định lý tổng ba góc trong tam giác)

Xét tam giác \(DHK\) có \(\widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \,\left( 2 \right)\) (định lý tổng ba góc trong tam giác)

Từ (1) và (2) suy ra \(\widehat {HCK} + \widehat {CHK} + \widehat {CKH} + \widehat {HDK} + \widehat {DHK} + \widehat {DKH} = 180^\circ \, + 180^\circ \, = 360^\circ \)

\( \Rightarrow \widehat {HCK} + \widehat {CHK} + \widehat {DHK} + \widehat {HDK} + \widehat {CKH} + \widehat {DKH} = 360^\circ \)

\( \Rightarrow \widehat {HCK} + \widehat {DHC} + \widehat {HDK} + \widehat {DKC} = 360^\circ \) mà \(\widehat {CHD} = 90^\circ ;\,\widehat {DKC} = 90^\circ ;\,\widehat {HCK} = 50^\circ \)

Suy ra \(\widehat {HDK} = 360^\circ  - 90^\circ  - 90^\circ  - 50^\circ  = 130^\circ \).