Cho tam giác \(ABC\) vuông cân tại \(A.\) Trên cạnh \(AB\) lấy điểm \(D,\) trên tia đối của tia \(AC\) lấy điểm \(E\) sao cho \(AE = AD.\) Kéo dài \(CD\) cắt \(BE\) tại \(I.\) Tính số đo góc \(\widehat {BIC}.\)

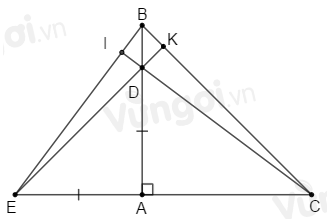
Gọi \(K\) là giao của \(ED\) và \(BC\).

\(\Delta ABC\) vuông cân tại \(A\) (gt) nên \(\widehat C = {45^o}\).

\(\Delta ADE\) có: \(\widehat {DAE} = {90^o};\,AD = AE\,\,(gt)\) nên \(\Delta ADE\) vuông cân tại \(A\) suy ra \(\widehat {AED} = {45^o}\) hay \(\widehat {CEK} = {45^o}.\)

Xét \(\Delta CEK\) có: \(\widehat C = \widehat {CEK} = {45^o}\,\,(cmt)\) suy ra \(\widehat {EKC} = {180^o} - \left( {\widehat C + \widehat {CEK}} \right) = {180^o} - \left( {{{45}^o} + {{45}^o}} \right) = {90^o}.\)

Vậy \(EK\, \bot \,BC.\)

Xét \(\Delta BCE\) có: \(BA\, \bot EC;\,EK \bot \,BC\) nên \(D\) là trực tâm của \(\Delta BCE\).

Suy ra \(CI\) là đường cao thứ ba của \(\Delta BCE\) hay \(CI\, \bot BE\).

Do đó \(\widehat {BIC} = {90^o}.\)