Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) cân tại \(A\) có: \(AH \bot BC\) tại \(H.\) Tính số đo góc \(BAH\) biết \(\widehat {BAC} = {50^0}.\)
Trả lời bởi giáo viên
Đáp án đúng: b
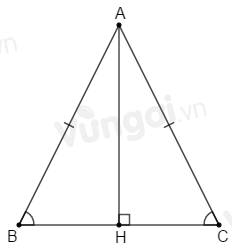
\(\Delta ABC\) cân tại \(A\), suy ra \(AB = AC;\,\,\widehat B = \widehat C\).
Xét hai tam giác vuông \(AHB\) và \(AHC\) có:
\(\widehat {AHB} = \widehat {AHC} = {90^o}\)
\(AB = AC\,\,(cmt)\)
\(\widehat B = \widehat C\,\,(cmt)\)
\( \Rightarrow \Delta AHB = \Delta AHC\,\) (cạnh huyền – góc nhọn).
\( \Rightarrow \widehat {BAH} = \widehat {CAH}\) (hai góc tương ứng).
Mặt khác: \(\widehat {BAH} + \widehat {CAH} = \widehat {BAC}\) suy ra \(\widehat {BAH} = \widehat {CAH} = \dfrac{{\widehat {BAC}}}{2} = \dfrac{{{{50}^o}}}{2} = {25^o}.\)
Hướng dẫn giải:
- Từ \(\Delta ABC\) cân tại \(A\), suy ra \(AB = AC;\,\widehat B = \widehat C\)
- Chứng minh \(\Delta AHB = \Delta AHC\) (cạnh huyền - góc nhọn) suy ra \(\widehat {BAH} = \widehat {CAH}\) (hai góc tương ứng).
- Mặt khác \(\widehat {BAH} + \widehat {CAH} = \widehat {BAC}\), từ đó tính được số đo \(\widehat {BAH.}\)
Câu hỏi khác
- Bài tập trường hợp bằng nhau thứ hai của tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ ba của tam giác toán 7 có lời giải
- Bài tập tổng ba góc của một tam giác toán 7 có lời giải
- Bài tập trường hợp bằng nhau thứ nhất của tam giác toán 7 có lời giải
- Bài tập hai tam giác bằng nhau toán 7 có lời giải
