Cho tam giác \(ABC\) vuông cân tại \(A\), có \(AC = 8cm.\) Một đường thẳng \(d\) bất kì luôn đi qua \(A\). Kẻ \(BH\) và \(CK\) lần lượt vuông góc với \(d\) tại \(H;\,K.\) Khi đó tổng \(B{H^2} + C{K^2}\) bằng:

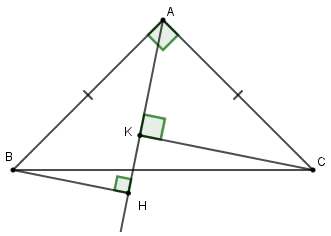
Vì \(\Delta ABC\) vuông cân tại \(A\) nên \(AB = AC\)  (tính chất)

Lại có: \(\widehat {ABH} + \widehat {BAH} = 90^\circ \) (vì \(\Delta ABH\) vuông tại \(H\)) và \(\widehat {CAH} + \widehat {BAH} = 90^\circ \)

Suy ra \(\widehat {ABH} = \widehat {CAK}\) (cùng phụ với \(\widehat {BAH}\)).

Xét \(\Delta ABH\) và \(\Delta CAK\) có:

\(AB = CA\,\,(cmt)\)

\(\widehat {AHB} = \widehat {CKA} = {90^o}\)

\(\widehat {ABH} = \widehat {CAK}\,\,(cmt)\)

\( \Rightarrow \Delta ABH = \Delta CAK\) (cạnh huyền-góc nhọn)

\( \Rightarrow BH = AK\) (hai cạnh tương ứng). 

Do đó \(B{H^2} + C{K^2} = A{K^2} + C{K^2}\,\,\left( 1 \right)\)

Áp dụng định lý Pytago vào tam giác vuông \(ACK\) có:  \(A{K^2} + C{K^2} = A{C^2}\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra: \(B{H^2} + C{K^2} = A{C^2} = {8^2} = 64\).